蓝桥杯-方格分割-dfs

Posted 2020-10-25 desserts

标题：方格分割

 

6x6的方格，沿着格子的边线剪开成两部分。

要求这两部分的形状完全相同。

 

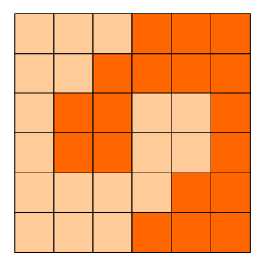
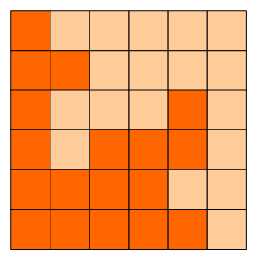
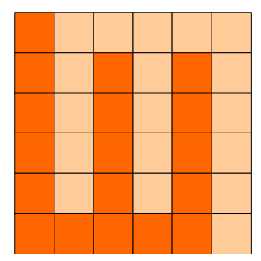
如图：p1.png, p2.png, p3.png 就是可行的分割法。

 

试计算：

包括这3种分法在内，一共有多少种不同的分割方法。

注意：旋转对称的 属于同一种分割法。

 

请提交该整数，不要填写任何多余的内容或说明文字。

      阿西吧，这道题真的是，绝望，本来的思路是分别从左上角和右下角各引出一条线路，按走过的表格数进行计算，忘记了dfs是一头撞到南墙不回头不能有岔路的那种，于是乎按照格子来走是不行了，去网上找了找大神的思路，果然是大神，我咋着就没有想到换个角度来看，不只是盯着表格，线呢！还有线呢！看线啊！还有人家是从中心开始的，中心是必经之路啊，无论怎样中心都是对称中心，真的是，最后，总结就是从中心兵分两路，沿线直到抵达边境，就算是一种结果，同样还是用dfs但是换了一个角度了。跪。还有就是注意点在于题上已经提示了旋转相同的只能算是一种结果，所以不要忘记除个4啊亲！都是一样的啊！委屈巴巴

#include<iostream>
using namespace std;
#define n 6
int board[n+1][n+1];
int cou =0;   //表示对称图形个数
struct coor{
    int i;
    int j;
};

coor direct1[4]= {{-1,0},{1,0},{0,-1},{0,1}},direct2[4] = {{1,0},{-1,0},{0,1},{0,-1}};
/*
答案509
思路：1、首先初始化棋盘未走过为0
      2、分析第一部分上下左右{(-1,0),(1,0),(0,-1),(0,1)}对称于第二部分下上右左{(1,0),(-1,0),(0,1),(0,-1)}
      3、两部分分别向四方进行试探，如果某方都没有走过则可将下一步置1，然后继续进行递归
*/

 void init()
 {
     for(int i=0;i<=n;i++)   //初始化棋盘
     {
         for(int j=0;j<=n;j++)
         {
             board[i][j] = 0;
         }
     }
     board[3][3] = 1;
 }

 bool check(coor next1,coor next2)   //检查此位置是否可以走，如果可以返回true
 {
     if(board[next1.i][next1.j] == 0&&board[next2.i][next2.j] == 0)
     {
         if(next1.i ==next2.i&&next1.j == next2.j){
             return false;
         }
         return true;
     }
     return false;
 }

void DFS(coor part1,coor part2)
{
    if(part1.i == 0||part1.j == 0||part1.j == n||part1.i == n)
    {
        ++cou;
        return ;
    }
    coor next1,next2;
    for(int i=0;i<4;i++)
    {
        next1.i= part1.i+direct1[i].i;
        next1.j= part1.j+direct1[i].j;
        next2.i= part2.i+direct2[i].i;
        next2.j= part2.j+direct2[i].j;

        if(check(next1,next2))
        {
            board[next1.i][next1.j] = board[next2.i][next2.j] = 1;//表示已经被走
            DFS(next1,next2);
            board[next1.i][next1.j] = board[next2.i][next2.j] = 0;
        }
    }
}

int main()
{
    coor start1,start2;
    start1.i = start1.j = 3;
    start2.i = start2.j = 3;
    init();
    DFS(start1,start2);
    cout<<cou/4;
    return 0;
}