BZOJ3527：[Zjoi2014]力——题解

Posted 2020-10-24

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了BZOJ3527：[Zjoi2014]力——题解相关的知识，希望对你有一定的参考价值。

http://www.lydsy.com/JudgeOnline/problem.php?id=3527

给出n个数qi，给出Fj的定义如下：

令Ei=Fi/qi，求Ei.

参考：https://www.cnblogs.com/iwtwiioi/p/4126284.html

暴力肯定会TLE，考虑转换成卷积形然后FFT优化。

（因为不是markdown所以算式截图自参考博客，如有不妥删……）

首先算E可以把F里的所有qj全部拿下，设f[i]=q[i]，g[i]=1/i/i（g[0]=0表示不存在这一项），显然可以变成：

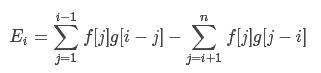
第一个变成卷积很简单，考虑将f所有存储值下标前移一位，同时n--。

所以j初值为0，末值为i，变成：f[j]g[i-j]。

对于后者，j初值为i，末值为n。

显然令j初值为0，末值t=n-i可以变成：f[j+i]g[j]

因为i=n-t，所以变成： f[j+n-t]g[j]

设ff[n-i]=f[i]，则f[j+n-t]=ff[t-j]。

所以变成： ff[t-j]g[j]。这是不是就是卷积了？

剩下的就是FFT基本功了。

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
typedef double dl;
const dl pi=acos(-1.0);
const int N=2e6+10;
struct complex{//定义复数 
    dl x,y;
    complex(dl xx=0.0,dl yy=0.0){
        x=xx;y=yy;
    }
    complex operator +(const complex &b)const{
        return complex(x+b.x,y+b.y);
    }
    complex operator -(const complex &b)const{
        return complex(x-b.x,y-b.y);
    }
    complex operator *(const complex &b)const{
        return complex(x*b.x-y*b.y,x*b.y+y*b.x);
    }
};
void FFT(complex a[],int n,int on){
    for(int i=1,j=n>>1;i<n-1;i++){
        if(i<j)swap(a[i],a[j]);
        int k=n>>1;
        while(j>=k){j-=k;k>>=1;}
        if(j<k)j+=k;
    }
    for(int i=2;i<=n;i<<=1){
        complex res(cos(-on*2*pi/i),sin(-on*2*pi/i));
        for(int j=0;j<n;j+=i){
            complex w(1,0);
            for(int k=j;k<j+i/2;k++){
                complex u=a[k],t=w*a[k+i/2];
                a[k]=u+t;
                a[k+i/2]=u-t;
                w=w*res;
            }
        }
    }
    if(on==-1)
        for(int i=0;i<n;i++)a[i].x/=n;
}
complex f[N],g[N],ff[N];
dl ans1[N],ans2[N];
int n;
int main(){
    scanf("%d",&n);n--;
    for(int i=0;i<=n;i++){
        scanf("%lf",&f[i].x);
        ff[n-i]=f[i];
    }
    for(int i=1;i<=n;i++)g[i].x=1.0/i/i;
    int len=1;
    while(len-1<n*2)len<<=1;
    FFT(f,len,1);FFT(ff,len,1);FFT(g,len,1);
    for(int i=0;i<len;i++){
        f[i]=f[i]*g[i];
        ff[i]=ff[i]*g[i];
    }
    FFT(f,len,-1);FFT(ff,len,-1);
    for(int i=0;i<len;i++)ans1[i]=f[i].x,ans2[i]=ff[i].x;
    for(int i=0;i<=n;i++)printf("%.3lf\\n",ans1[i]-ans2[n-i]);
    return 0;
}

+++++++++++++++++++++++++++++++++++++++++++

+本文作者：luyouqi233。　　　　　　　　　　　　　　+

+欢迎访问我的博客：http://www.cnblogs.com/luyouqi233/+

+++++++++++++++++++++++++++++++++++++++++++

以上是关于BZOJ3527：[Zjoi2014]力——题解的主要内容，如果未能解决你的问题，请参考以下文章

bzoj3527: [Zjoi2014]力

BZOJ[3527]，[ZJOI2014]力（FFT）

●BZOJ 3527 [Zjoi2014]力

bzoj3527: [Zjoi2014]力卷积+FFT

BZOJ 3527: [Zjoi2014]力