cf 460 E. Congruence Equation 数学题

Posted 2020-10-23 jiachin_zhao

cf 460 E. Congruence Equation 数学题

题意:

给出一个x 计算<=x的满足下列的条件正整数n的个数

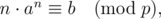
\(p是素数,2?≤?p?≤?10^{6}?+?3, 1?≤?a,?b?<?p, 1?≤?x?≤?10^{12}\)

思路:

题目中存在两个循环节 \(n % p\) 和 \(a ^ n % p\), 循环节分别为\(p,p-1\)
我们枚举\(i = n\ (mod)\ (p - 1)\)
可以得到两个方程
\[ n\ \equiv\ i\ mod\ (p-1) \]
\[ n \equiv \frac{b}{a ^ i}\ mod\ p\]

令$mm = \frac{b}{a ^ i} $
设 \[n = p * k + mm , n = (p - 1) * q + i \]
于是\(p * k + mm = p * q - q + i\)
在模p意义下可以得到
\(q \equiv (i - mm)\ (mod) p\)

然后就可以根据限制条件计算出有多少个满足条件的q 即答案了

#include<bits/stdc++.h>
#define LL long long
using namespace std;

LL qpow(LL x,LL y,LL mod){
    x %= mod;
    LL ans = 1;
    while(y){
        if(y & 1) ans = ans * x % mod;
        x = x * x % mod;
        y >>= 1;
    }
    return ans;
}
int main(){

    LL a,b,p,X;
    cin>>a>>b>>p>>X;
    LL x,y,m = b,inva = qpow(a, p - 2,p);
    LL ans = 0;
    for(int i = 0;i < p - 1;i++){
        LL mm = (i - m + p) % p;
        LL R = (floor)((1.0 * (X - i) / (p -1) - mm)/p) ;
        LL L = mm / p;
       // for(int j = L;j <= R;j++) cout<<(p * j + mm) * (p - 1) + i<<" ";
        m = m * inva % p;
        ans += R - L + 1;
    }
    cout<<ans<<endl;
    return 0;
}