[CF460E]Roland and Rose

Posted 2020-10-16

题意：给定$n$和$r$，要找$n$个整点，使得他们两两距离的平方和最大，并且所有点到原点的距离必须小于$r$

很容易猜到答案在凸包上然后暴力找，但证明还是挺妙的

首先转化一下距离平方和

令$\\vec{a_i}=\\vec{OA_i}$，则$\\sum\\limits_{i\\lt j}A_iA_j^2=\\dfrac{\\sum\\limits_{i\\neq j}A_iA_j^2}{2}=\\dfrac{\\sum\\limits_{i\\neq j}(\\vec{a_i}-\\vec{a_j})^2}{2}=\\dfrac{\\sum\\limits_{i\\neq j}(\\vec{a_i}^2+\\vec{a_j}^2-2\\cdot\\vec{a_i}\\cdot\\vec{a_j})}{2}$

对于每个$k$，当$i=k$时$\\vec{a_k}^2$被计算$n-1$次，当$i\\neq k$时被计算$n-1$次

再用和的平方公式处理一下两两做点积的项

原式$=\\dfrac{2(n-1)\\sum\\limits_{1\\leq i\\leq n}\\vec{a_i}^2-2[(\\sum\\limits_{1\\leq i\\leq n}\\vec{a_i})^2-\\sum\\limits_{1\\leq i\\leq n}\\vec{a_i}^2]}{2}=n\\sum\\limits_{1\\leq i\\leq n}\\vec{a_i}^2-(\\sum\\limits_{1\\leq i\\leq n}\\vec{a_i})^2$

为了让第一项尽可能大，选的点应该尽可能远离原点，为了让第二项尽可能小，选的点应该尽可能可以互相抵消（因为是向量和）

这提示了我们答案会分布在凸包上，下面我们来严格证明

假设已经确定了$A_{1\\cdots n-1}$我们想确定最后一个点，设它为$P(x,y)$

新增加的距离平方和为$\\sum\\limits_{1\\leq i\\leq n-1}[(x-x_i)^2+(y-y_i)^2]$

整理一下，得到$(n-1)[(x-\\frac{\\sum\\limits_{1\\leq i\\leq n-1}x_i}{n-1})^2-(\\frac{\\sum\\limits_{1\\leq i\\leq n-1}x_i}{n-1})^2+\\frac{\\sum\\limits_{1\\leq i\\leq n-1}x_i^2}{n-1}+(y-\\frac{\\sum\\limits_{1\\leq i\\leq n-1}y_i}{n-1})^2-(\\frac{\\sum\\limits_{1\\leq i\\leq n-1}y_i}{n-1})^2+\\frac{\\sum\\limits_{1\\leq i\\leq n-1}y_i^2}{n-1}]$

后面那一大坨东西跟$x,y$无关，所以问题转换为求离$X(\\dfrac{\\sum\\limits_{1\\leq i\\leq n-1}x_i}{n-1},\\dfrac{\\sum\\limits_{1\\leq i\\leq n-1}y_i}{n-1})$最远的点

下面证$P$在凸包端点上

假设$P$不在凸包端点上，延长$XP$与凸包某边$AB$交于$P‘$（交于端点直接取端点为更优解）

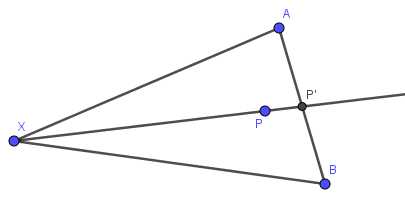
若$\\angle AP‘X\\geq\\dfrac{\\pi}{2}$，则$AX\\gt XP‘\\gt XP$，即选$A$更优

若$\\angle BP‘X\\geq\\dfrac{\\pi}{2}$，则$BX\\gt XP‘\\gt XP$，即选$B$更优

就这样证完了

所以一开始找一下凸包，然后暴力找到最优解

算一下就知道$r=29$的时候凸包的点数量最多，有$36$个，一点都不虚其实还是得感谢CF的评测机

我居然能找到一道Div2的E是暴力23333

#include<stdio.h>
#include<math.h>
#include<vector>
using namespace std;
struct point{
	int x,y;
	point(int a=0,int b=0){
		x=a;
		y=b;
	}
}t;
point operator-(point a,point b){
	return point(a.x-b.x,a.y-b.y);
}
int operator*(point a,point b){
	return a.x*b.y-a.y*b.x;
}
vector<point>p;
vector<int>now,bes;
int n,r,ans;
void dfs(int chos,int las,int sx,int sy,int sx2,int sy2){
	if(chos==n){
		if(ans<n*(sx2+sy2)-sx*sx-sy*sy){
			ans=n*(sx2+sy2)-sx*sx-sy*sy;
			bes=now;
		}
		return;
	}
	for(int i=las;i<p.size();i++){
		now.push_back(i);
		dfs(chos+1,i,sx+p[i].x,sy+p[i].y,sx2+p[i].x*p[i].x,sy2+p[i].y*p[i].y);
		now.pop_back();
	}
}
int main(){
	scanf("%d%d",&n,&r);
	int i,s;
	for(i=-r;i<=0;i++){
		p.push_back(point(i,(int)sqrt(r*r-i*i)));
		while(p.size()>2&&(p[p.size()-2]-p[p.size()-3])*(p[p.size()-1]-p[p.size()-2])>=0){
			p[p.size()-2]=p[p.size()-1];
			p.pop_back();
		}
	}
	s=p.size();
	for(i=s-2;i>=0;i--)p.push_back(point(-p[i].x,p[i].y));
	for(i=1;i<s;i++)p.push_back(point(-p[i].x,-p[i].y));
	for(i=s-2;i>0;i--)p.push_back(point(p[i].x,-p[i].y));
	ans=0;
	dfs(0,0,0,0,0,0);
	printf("%d\\n",ans);
	for(i=0;i<n;i++)printf("%d %d\\n",p[bes[i]].x,p[bes[i]].y);
}