LCA最近公共祖先
Tarjan他贱(离线)算法的基本思路及其算法实现
本文是网络资料整理或部分转载或部分原创,参考文章如下:
https://www.cnblogs.com/JVxie/p/4854719.html
http://blog.csdn.net/ywcpig/article/details/52336496
https://baike.baidu.com/item/最近公共祖先/8918834?fr=aladdin
最近公共祖先简称LCA(Lowest Common Ancestor):
所谓LCA:是当给定一个有根树T时,对于任意两个结点u、v,找到一个离根最远的结点x,使得x同时是u和v的祖先,x 便是u、v的最近公共祖先。
再通俗地解释一下:在一棵没有环的树上,每个节点肯定有其父亲节点和祖先节点,而最近公共祖先,就是两个节点在这棵树上深度最大的公共的祖先节点。换句话说,就是两个点在这棵树上距离最近的公共祖先节点。所以LCA主要是用来处理当两个点仅有唯一一条确定的最短路径时的路径。LCA还可以将自己视为祖先节点。
本文为了简化,多使用二叉树来讨论。
举个例子,如针对下图所示的一棵普通的二叉树来讲:
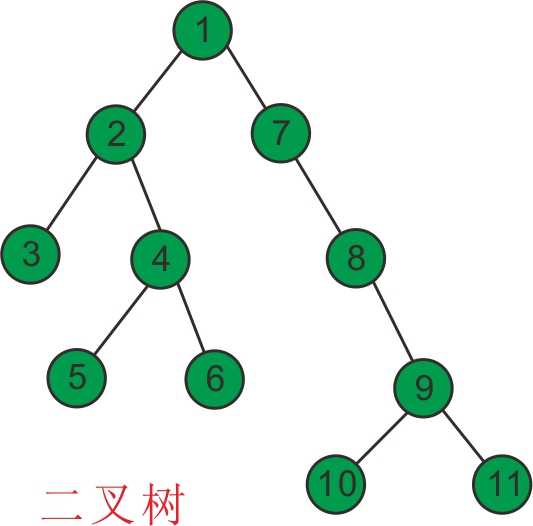
结点3和结点4的最近公共祖先是结点2,即LCA(3,4)=2 。
需要注意到当两个结点在同一棵子树上的情况。
如结点3和结点2的最近公共祖先为2,即 LCA(3,2)=2。
同理:LCA(5,6)=4,LCA(6,10)=1。
明确了题意,咱们便来试着解决这个问题。直观的做法,可能是针对是否为二叉查找树分情况讨论,这也是一般人最先想到的思路。除此之外,还有Tarjan算法、倍增算法、以及转换为RMQ问题(求某段区间的极值)。
我们先来讲讲暴力解法:
解法一:如果是二叉查找树,如下图:
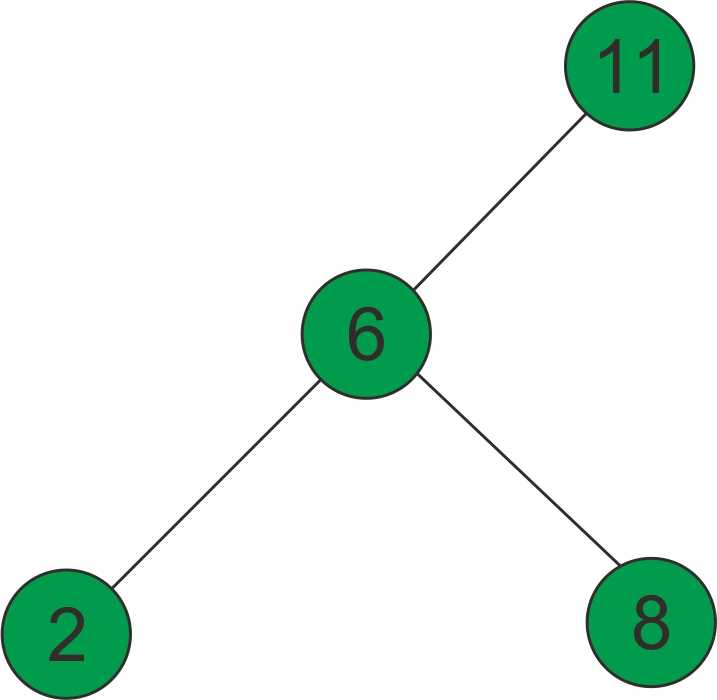
那么从树根开始:
- 如果当前结点t 大于结点u、v,说明u、v都在t 的左侧,所以它们的共同祖先必定在t 的左子树中,故从t 的左子树中继续查找;
- 如果当前结点t 小于结点u、v,说明u、v都在t 的右侧,所以它们的共同祖先必定在t 的右子树中,故从t 的右子树中继续查找;
- 如果当前结点t 满足 u <t < v,说明u和v分居在t 的两侧,故当前结点t 即为最近公共祖先;
- 而如果u是v的祖先,那么u就是最近公共祖先,同理,如果v是u的祖先,那么v就是最近公共祖先。
伪代码如下所示:
int query(Node t, Node u, Node v) {
int left = u.value;
int right = v.value;
//二叉查找树内,如果左结点大于右结点,就交换。不知道为什么要交换
if (left > right) {
int temp = left;
left = right;
right = temp;
}
while (true) {
//如果t小于u、v,往t的右子树中查找
if (t.value < left) {
t = t.right;
//如果t大于u、v,往t的左子树中查找
} else if (t.value > right) {
t = t.left;
} else {
return t.value;
}
}
}
如果不是二叉查找树,对于每个询问,就暴力遍历所有的点,时间复杂度为O(n*q),q是询问的次数。很明显,n和q一般不会很小。此处略......
解法二:Tarjan(离线)算法解决LCA
离线算法就是指统一输入后再统一输出,而不是边输入边实时输出。Tarjan算法的复杂度为O(N+Q),Q为询问的次数。相当于一次性批量处理,一开始就知道了全部查询,只待询问。
下面详细介绍一下Tarjan算法的基本思路:看不明白没关系,我们后面会模拟的。
1.任选一个点为根节点,从根节点开始。
2.遍历该点u所有子节点v,并标记这些子节点v已被访问过。
3.若是v还有子节点,返回2,否则下一步。
4.合并v到u上。
5.寻找与当前点u有询问关系的点v。
6.若是v已经被访问过了,则可以确认u和v的最近公共祖先为v被合并到的父亲节点a。
遍历的话需要用到dfs来遍历,至于合并,最优化的方式就是利用并查集来合并两个节点。
下面上伪代码:


Tarjan(u) //marge和find为并查集合并函数和查找函数
{
for each(u,v) //访问所有u的子节点v
{
Tarjan(v); //继续往下遍历
marge(u,v); //合并v到u上, 标记v被访问过;
}
for each(u,e) //访问所有和u有询问关系的e
{
如果e被访问过; u,e的最近公共祖先为find(e);
}
}
我们先来直接模拟一下用Tarjan来解决LCA,然后再总结。
假设我们有一组数据 9个节点 8条边 联通情况如下:
1--2,1--3,2--4,2--5,3--6,5--7,5--8,7--9 即下图所示的树
设我们要查找最近公共祖先的点为9和8,4和6,7和5,5和3;
设f[]数组为并查集的父亲节点数组,初始化f[i]=i,vis[]数组为是否访问过的数组,初始为0;
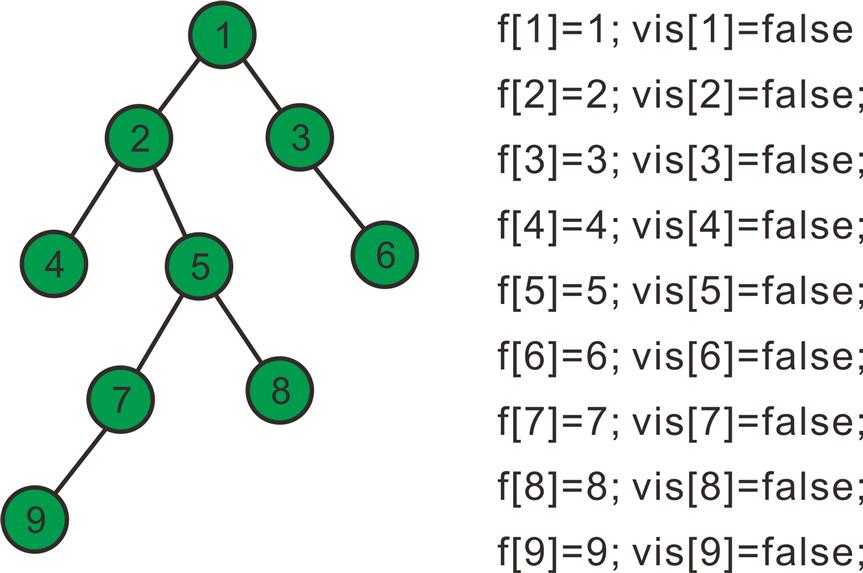
下面开始模拟过程:
取1为根节点,往下搜索发现有两个儿子2和3;
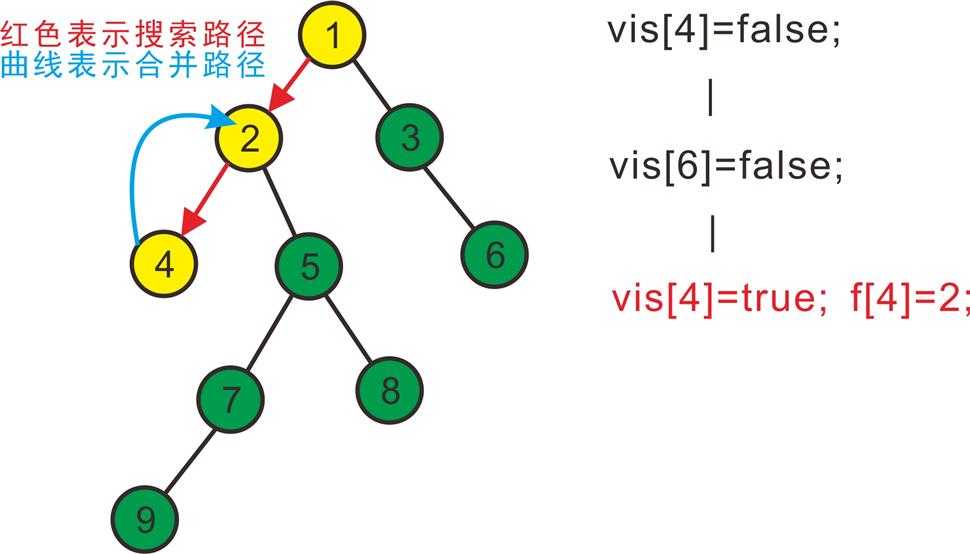
先搜2,发现2有两个儿子4和5,先搜索4,发现4没有子节点,则寻找与其有关系的点;
发现6与4有关系,但是vis[6]=false,即6还没被搜过,所以不操作;
发现没有和4有询问关系的点了,返回此前一次搜索,更新vis[4]=true,表示4已经被搜完,再更新f[4]=2,表示4被合并到2,如下图:
继续搜5,发现5有两个儿子7和8;
先搜7,发现7有一个子节点9,搜索9,发现没有子节点,寻找与其有关系的点;
发现8和9有关系,但是vis[8]=false,即8没被搜到过,所以不操作;
发现没有和9有询问关系的点了,返回此前一次搜索,更新vis[9]=true;
表示9已经被搜完,更新f[9]=7;
回到7,发现7没有没被搜过的子节点了,寻找与其有关系的点;
发现5和7有关系,但是vis[5]=false,所以不操作;
发现没有和7有关系的点了,返回此前一次搜索,更新vis[7]=true;
表示7已经被搜完,更新f[7]=5。如下图:
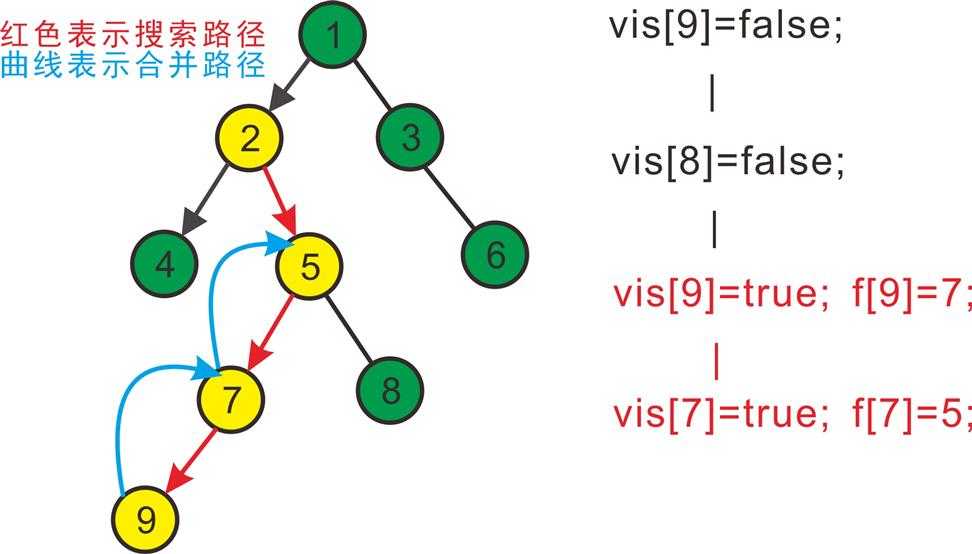
继续搜8,发现8没有子节点,则寻找与其有关系的点;
发现9与8有关系,此时vis[9]=true,则他们的最近公共祖先为find(9)=5;(此处好好想一想)
find(9)的顺序为f[9]=7-->f[7]=5-->f[5]=5 return 5;
发现没有与8有关系的点了,返回此前一次搜索,更新vis[8]=true;
表示8已经被搜完,更新f[8]=5。如下图:
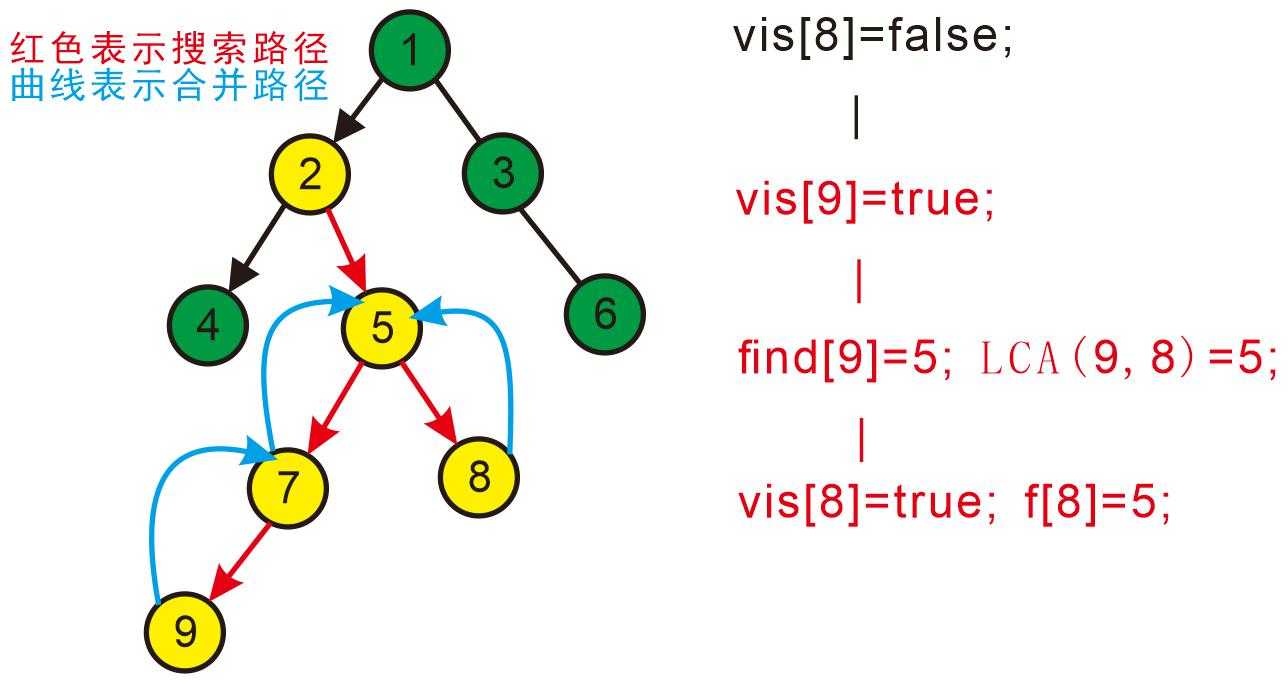
回到5发现5也没有没搜过的子节点了,寻找与其有关系的点;
发现7和5有关系,此时vis[7]=true,所以他们的最近公共祖先为find(7)=5;
find(7)的顺序为f[7]=5-->f[5]=5 return 5;
又发现5和3有关系,但是vis[3]=false,所以不操作,此时5的子节点全部搜完了;
返回此前一次搜索,更新vis[5]=true,表示5已经被搜完,更新f[5]=2;
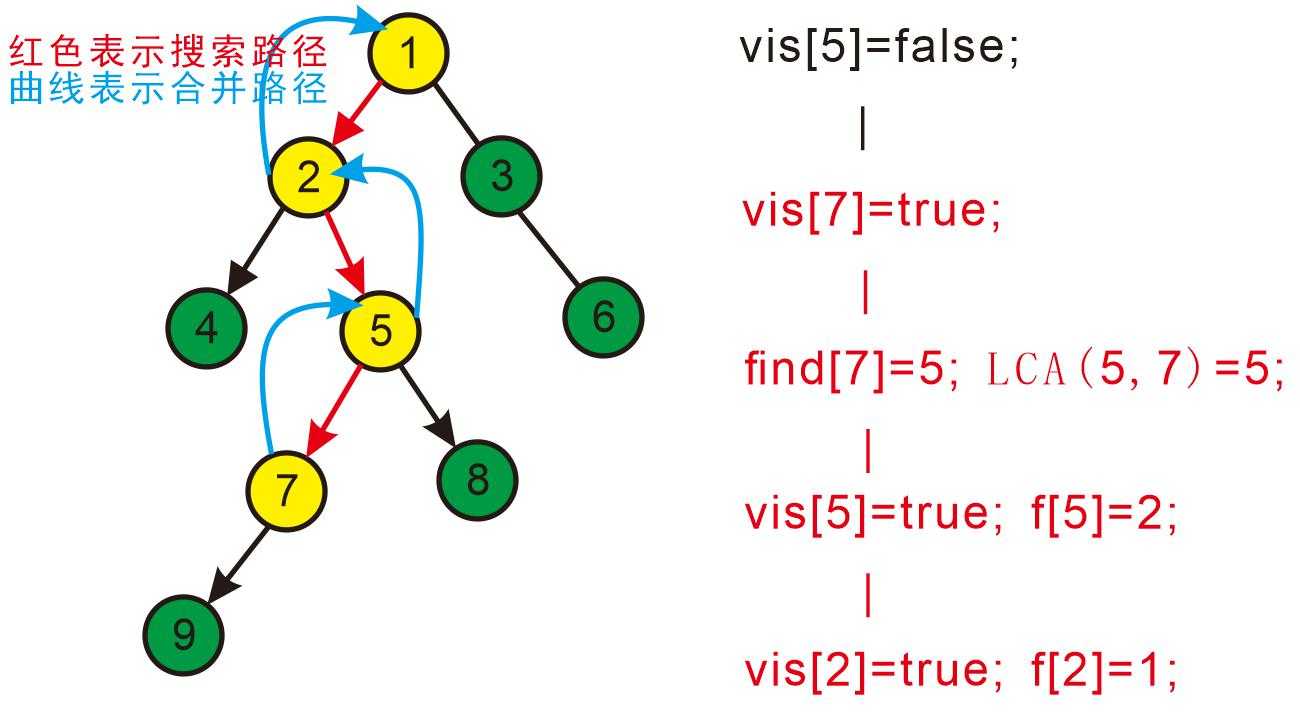
回到2发现2没有未被搜完的子节点,寻找与其有关系的点;
发现没有和2有关系的点,返回此前一次搜索,更新vis[2]=true;
表示2已经被搜完,更新f[2]=1。如下图:
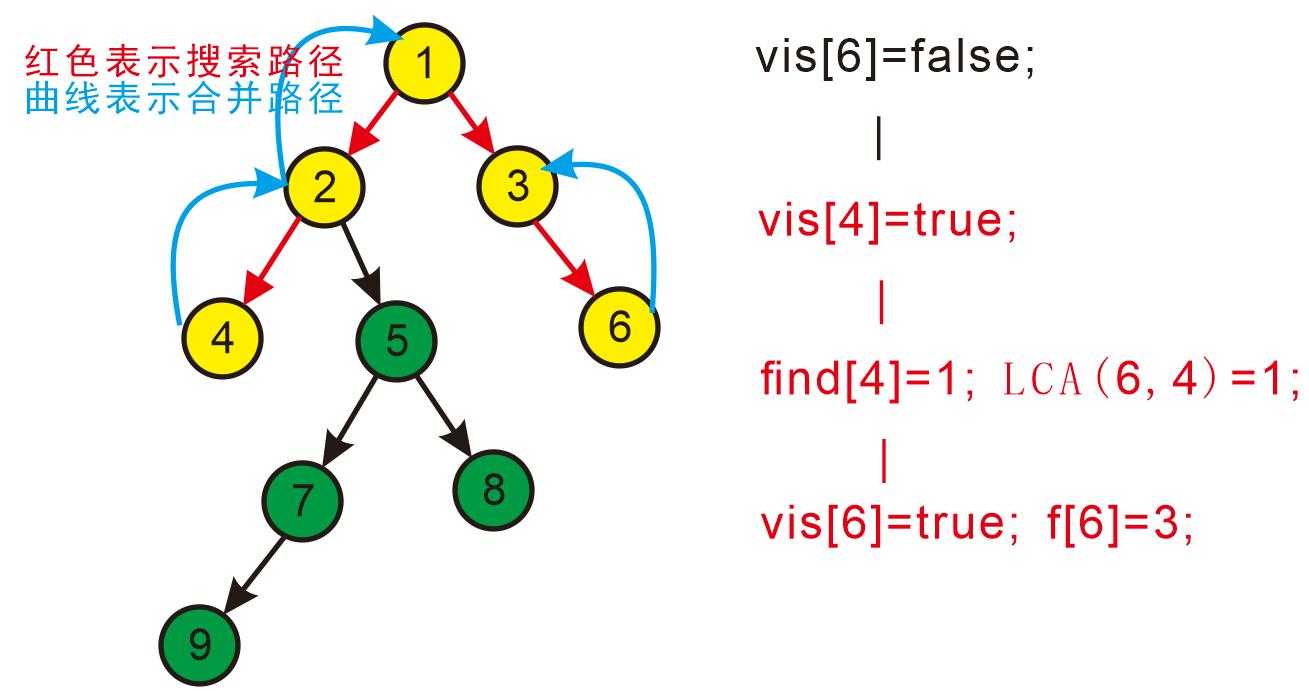
接着搜3,发现3有一个子节点6;
搜索6,发现6没有子节点,则寻找与6有关系的点,发现4和6有关系;
此时vis[4]=true,所以它们的最近公共祖先为find(4)=1;
find(4)的顺序为f[4]=2-->f[2]=1-->f[1]=1 return 1;
发现没有与6有关系的点了,返回此前一次搜索,更新vis[6]=true,表示6已经被搜完了;
更新f[6]=3。如下图:
回到3发现3没有没被搜过的子节点了,则寻找与3有关系的点;
发现5和3有关系,此时vis[5]=true,则它们的最近公共祖先为find(5)=1;
find(5)的顺序为f[5]=2-->f[2]=1-->f[1]=1 return 1;
发现没有和3有关系的点了,返回此前一次搜索,更新vis[3]=true;更新f[3]=1。
如下图:
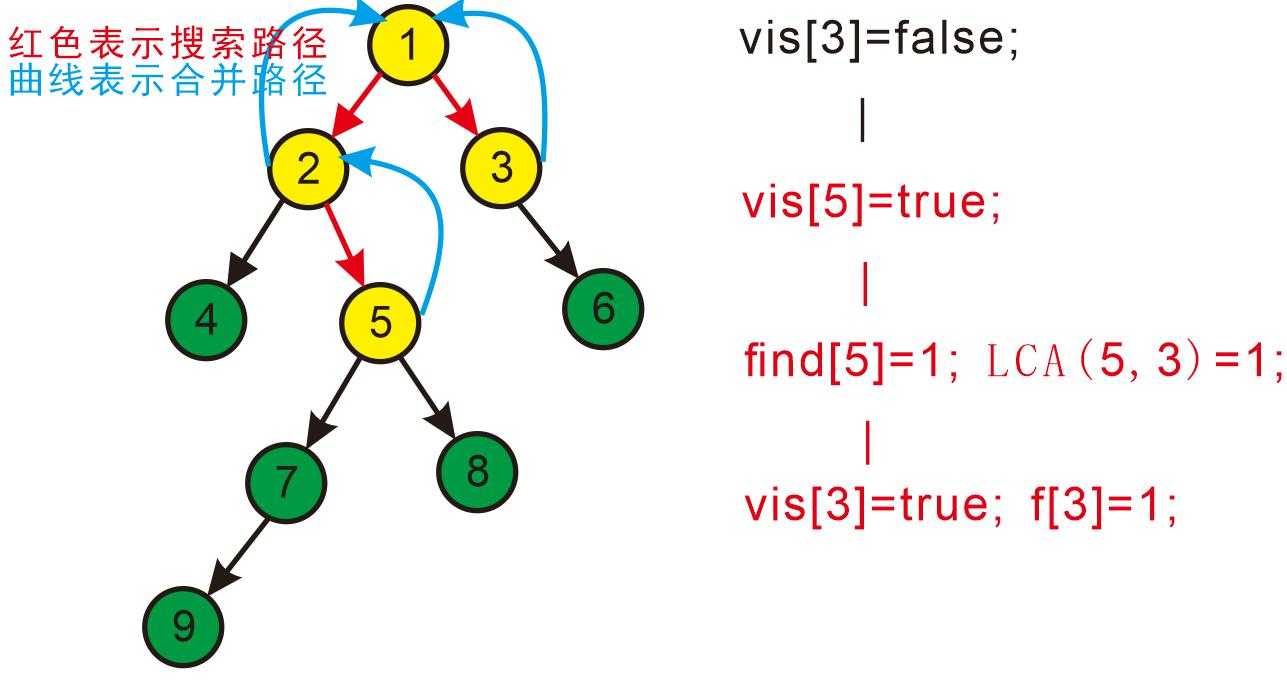
最后发现1没有被搜过的子节点也没有有关系的点,此时可以退出整个dfs了。
经过这次dfs我们得出了所有的答案。
总结:
Tarjan离线算法,将所求先储存,然后结合并查集和DFS,
如果所求的两个点都vis[]==1,那么输出他们的father
P3379 【模板】最近公共祖先(LCA)
https://www.luogu.org/problemnew/show/3379
2370 小机房的树
http://codevs.cn/problem/2370/
1036 商务旅行
http://codevs.cn/problem/1036/
LCA Tarjan算法模板 参考代码C++
https://www.luogu.org/problemnew/solution/P3379 最后一个
https://www.cnblogs.com/fish7/p/4006056.html
http://blog.csdn.net/qq_24451605/article/details/43114243
http://blog.csdn.net/mzyupengju/article/details/47146789
http://blog.csdn.net/tekim/article/details/77750093
https://www.cnblogs.com/jsawz/p/6723221.html