LCA（最近公共祖先）——离线 Tarjan 算法

Posted 2020-09-29 GGBeng

tarjan算法的步骤是(当dfs到节点u时):
1 在并查集中建立仅有u的集合,设置该集合的祖先为u
1 对u的每个孩子v:
   1.1 tarjan之
   1.2 合并v到父节点u的集合,确保集合的祖先是u
2 设置u为已遍历
3 处理关于u的查询,若查询(u,v)中的v已遍历过,则LCA(u,v)=v所在的集合的祖先

不懂请点击

 伪代码：

Tarjan(u)//marge和find为并查集合并函数和查找函数
{
    for each(u,v)    //访问所有u子节点v
    {
        Tarjan(v);        //继续往下遍历
        marge(u,v);    //合并v到u上
        标记v被访问过;
    }
    for each(u,e)    //访问所有和u有询问关系的e
    {
        如果e被访问过;
        u,e的最近公共祖先为find(e);
    }
}

模板：

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<vector>
  4 #include<algorithm>
  5 using namespace std;
  6 const int maxn = 10010;
  7 
  8 int rank[maxn];            //并查集结点高度 
  9 int pre[maxn];            //并查集父节点 
 10 int anc[maxn];            //祖先 
 11 int indgree[maxn];        //保存每个节点的入度 
 12 bool vis[maxn]; 
 13 vector<int> tree[maxn];    //保存树
 14 vector<int> qes[maxn];    //保存查询 
 15 int vertex_num;            //顶点数 
 16 
 17 void init()
 18 {
 19     memset(rank,1,sizeof(rank));
 20     memset(vis,0,sizeof(vis));
 21     memset(indgree,0,sizeof(indgree));
 22     memset(anc,0,sizeof(anc));
 23     for(int i=1;i<=vertex_num;i++){
 24         pre[i] = i;
 25         tree[i].clear();
 26         qes[i].clear();
 27     }
 28 }
 29 
 30 int find_pre(int x)        //查找函数 
 31 {
 32     if(pre[x] == x){
 33         return x;
 34     }
 35     else{
 36         pre[x] = find_pre(pre[x]);        //压缩路径 
 37     }
 38     return pre[x];
 39 }
 40 
 41 void Union(int x,int y)
 42 {
 43     x = find_pre(x);
 44     y = find_pre(y);
 45     if(x == y){
 46         return ;
 47     }
 48     else{
 49         if(rank[x] > rank[y]){
 50             pre[y] = x;
 51         }
 52         else if(rank[x] == rank[y]){        //x和y深度相同时， y向x合并 
 53             rank[x]++;
 54             pre[y] = x;
 55         }
 56         else{
 57             pre[x] = y;
 58         }
 59     }
 60 }
 61 
 62 int lca(int u)
 63 {
 64     anc[u] = u;
 65     for(int i=0;i<tree[u].size();i++){
 66         lca(tree[u][i]);
 67         Union(u,tree[u][i]);
 68         anc[find_pre(u)]=u;
 69     } 
 70     vis[u] = 1;
 71     for(int i=0;i<qes[u].size();i++){
 72         if(vis[qes[u][i]] == 1){
 73             return anc[find_pre(qes[u][i])];
 74         }
 75     }
 76 }
 77 
 78 int main()
 79 {
 80     cout<<"请输入顶点数："; 
 81     cin>>vertex_num;
 82     init();
 83     int u,v,ans;
 84     cout<<"请依次输入各边：\\n";
 85     for(int i=1;i<vertex_num;i++){
 86         cin>>u>>v;
 87         tree[u].push_back(v);
 88         indgree[v]++; 
 89     }
 90     cout<<"请输入要查询的两个数：";
 91     cin>>u>>v;
 92     qes[u].push_back(v);
 93     qes[v].push_back(u);
 94     for(int i=1;i<=vertex_num;i++){
 95         if(indgree[i] == 0){
 96             ans = lca(i);
 97             printf("(%d,%d)的LCA是：%d\\n",u,v,ans);
 98             break;
 99         }
100     }
101     return 0;
102 }

上一个图，来测试模板：

 

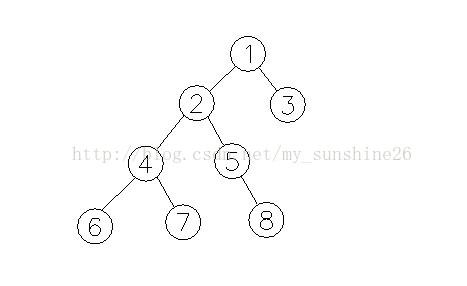
题目：POJ 1470

代码：点击

/* 
 * POJ 1470 
 * 给出一颗有向树，Q个查询 
 * 输出查询结果中每个点出现次数 
 */ 
/* 
 * LCA离线算法，Tarjan 
 * 复杂度O(n+Q); 
 */