第3章线性回归

Posted 2020-10-21 weiququ

1. 简单线性回归

     方程式：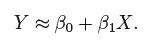

 

    

 

 

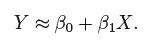
 1.1 估计参数

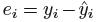代表第i 个残差第i 个观测到的响应值和第i 个用线性模型预测出的响应值之间的差距

残差平方和（residual sum of squares ,RSS）：

                         

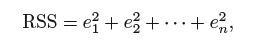
等价于：

                   

 

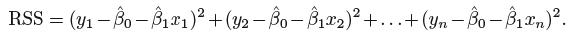
最小二乘法选择β0和β1来使RSS达到最小。通过微积分运算，使RSS最小的参数估计值为：

                      

 

 

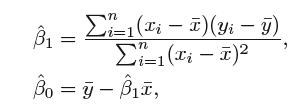
1.2评估系数估计值的准确性

X和Y之间的真实关系为：，其中是均值为零的随机误差项，

样本均值μ^ 的标准误差(standard error ，写作SE(μ^) )：

　　　　　　　　

 

其中， σ 是变量Y 的每个实现值Yi 的标准差。标准误差告诉我们估计μ^偏离μ的实际值的平均量。

计算β0和β1 的标准误差：

　　　　　　

 

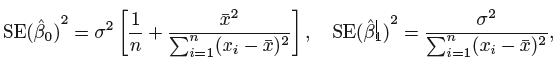
其中

对的估计被称为残差标准差

 

 标准误差可用于计算置信区间。β1 的95% 置信区间约为: 

 

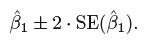
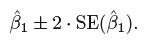
β0的95% 置信区间约为: 

 

标准误差也可以用来对系数进行假设检验：

　　

 

t统计量：

　　

 

p-value很小的时候拒绝零假设，X和Y之间存在关系。典型的拒绝零假设的临界p 值是5% 或1%

 

1.3评价模型的准确性

 

判断线性回归的拟合质量通常用两个相关的量：残差标准差（RSE）和R^2统计量。

残差标准差计算公式：

　　

 

R^2 统计量衡量了X 和Y 之间的线性关系。相关性的定义为：

　　

 

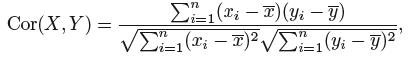
r = Cor(X,Y) ，在简单的线性回归中r^2 = R^2

 

 

2. 多元线性回归

 

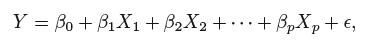
2.1 估计回归系数

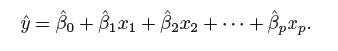
同样使用最小二乘法来进行参数的估计，选择β0, β1, . . . , βp使残差平方和最小:

　　

　　

 

 

 

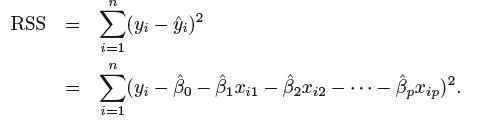
（1）假设检验：

 

 

当响应变量与预测变量无关， F 统计量应该接近1 。一个较大的F 统计量表明，至少有一个广告媒体与sales 相关

 

（2）选定重要变量

向前选择、向后选择、混合选择

向前选择：从零模型开始，建立简单的线性回归模型，并把使RSS 最小的变量添加到零模型中。然后再加入一个新变量，得到新的双变量模型，加人的变量是使新模型的RSS 最小的变量。这一过程持续到满足某种停止规则为止。

向后选择：从包含所有变量的模型开始，并删除p值最大的变量，再重新拟合，再删除p值最大的变量，持续到满足某种停止规则为止

 

3. 回归模型中的注意事项

（1）outlier离群点：Yi 远离模型预测值的点，如图中的点20

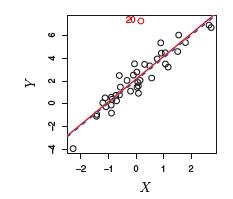
（2）High Leverage Points高杠杆点： 表示观测点X i是异常的，如图中的点41

（3）共线性

共线性( collinearity) 是指两个或更多的预测变量高度相关。

使用方差膨胀因子(variance inflation factor , VIF)来评估多重共线性：

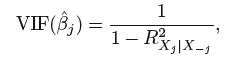
 解决办法：

1.从回归中剔除一个问题变量

2.把共线变量组合成一个单一的预测变量