想象一下,要搞掉一个植物,必须先搞掉另一些植物……我们可以发现这是一个最大权闭合子图的问题。
最大权闭合子图的话,太空飞行计划问题是一个入门题,可以一看。
然而我们手玩一下样例就会惊恐地发现,保护关系出现了环。
比如说:
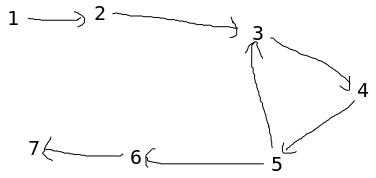
从 i 到 j 的箭头是说要搞 i 就要先搞 j,这是为了和最大权闭合子图的模型对应。
要搞 3 就要先搞 4,要搞 4 就要先搞 5,要搞 5 就要先搞 3……简直是乱来……
这就像是一个无冷却食人花前面放一个坚果
所以就要删环了,把边倒过来拓扑排序一下,能被拓扑到的点就是合法的点。
然后就按照最大权闭合子图的套路搞一搞就是了。
记得开当前弧优化
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
using namespace std;
int n, m, src[25][35], oea[605], ont, uu, vv, ind[605], ss, tt, tot, maxFlow, cnt, hea[605];
int lev[605], cur[605];
const int oo=0x3f3f3f3f;
queue<int> d;
bool vis[605];
struct Odge{
int too, nxt;
}odge[370005];
struct Edge{
int too, nxt, val;
}edge[800005];
int f(int i, int j){
return (i-1)*m+j;
}
void add_odge(int fro, int too){
odge[++ont].nxt = oea[fro];
odge[ont].too = too;
oea[fro] = ont;
}
void add_edge(int fro, int too, int val){
edge[cnt].nxt = hea[fro];
edge[cnt].too = too;
edge[cnt].val = val;
hea[fro] = cnt++;
}
void addEdge(int fro, int too, int val){
add_edge(fro, too, val);
add_edge(too, fro, 0);
}
void topsort(){
for(int i=1; i<=n*m; i++)
if(!ind[i])
d.push(i);
while(!d.empty()){
int x=d.front();
d.pop();
vis[x] = true;
for(int i=oea[x]; i; i=odge[i].nxt){
int t=odge[i].too;
ind[t]--;
if(!ind[t])
d.push(t);
}
}
}
bool bfs(){
memset(lev, 0, sizeof(lev));
lev[ss] = 1;
d.push(ss);
while(!d.empty()){
int x=d.front();
d.pop();
for(int i=hea[x]; i!=-1; i=edge[i].nxt){
int t=edge[i].too;
if(!lev[t] && edge[i].val>0){
lev[t] = lev[x] + 1;
d.push(t);
}
}
}
return lev[tt]!=0;
}
int dfs(int x, int lim){
if(x==tt) return lim;
int addFlow=0;
for(int &i=cur[x]; i!=-1; i=edge[i].nxt){
int t=edge[i].too;
if(lev[t]==lev[x]+1 && edge[i].val>0){
int tmp=dfs(t, min(lim-addFlow, edge[i].val));
edge[i].val -= tmp;
edge[i^1].val += tmp;
addFlow += tmp;
if(addFlow==lim) break;
}
}
return addFlow;
}
void dinic(){
while(bfs()){
for(int i=ss; i<=tt; i++) cur[i] = hea[i];
maxFlow += dfs(ss, oo);
}
}
int main(){
memset(hea, -1, sizeof(hea));
cin>>n>>m;
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++){
scanf("%d", &src[i][j]);
int tmp;
scanf("%d", &tmp);
while(tmp--){
scanf("%d %d", &uu, &vv);
uu++; vv++;
add_odge(f(i,j), f(uu,vv));
ind[f(uu,vv)]++;
}
if(j>1) add_odge(f(i,j), f(i,j-1)), ind[f(i,j-1)]++;
}
topsort();
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
if(vis[f(i,j)])
for(int k=oea[f(i,j)]; k; k=odge[k].nxt){
int t=odge[k].too;
if(vis[t])
addEdge(t, f(i,j), oo);
}
ss = 0; tt = n * m + 1;
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
if(vis[f(i,j)]){
if(src[i][j]>=0) addEdge(ss, f(i,j), src[i][j]), tot += src[i][j];
else addEdge(f(i,j), tt, -src[i][j]);
}
dinic();
cout<<max(tot-maxFlow, 0)<<endl;
return 0;
}