数值分析

Posted 2020-10-20 Mr y

Preface:数值分析（计算问题！）

应试教会了我们要好好学习，或者对于我这样的学渣来说，不得不学习，但终归还是学到了一些东(tao)西(lu)，但考完感觉空空的，想反思和总结下所学所得，为一些不为什么而留下一些有趣的灵魂

但不论是否应试，多理解和思考才能得道，用一遍遍的手抄课本知识点和笔记来逃避问题始终像是在核心思考周边打转，复制粘贴解无大用，思考出真知，复制粘贴解无大用，思考出真知，复制粘贴解无大用，思考出真知，并不能做到牵一发而动全身，更谈不上自己学习的初衷：用所学解决和思考所遇问题。

当然，会当凌绝顶，一览众山小，只有站在更高的地方才会对所学信手拈来，而站在更高的地方，刷题是必须的，只有多多做题才能矫正和加深理解。

---

 

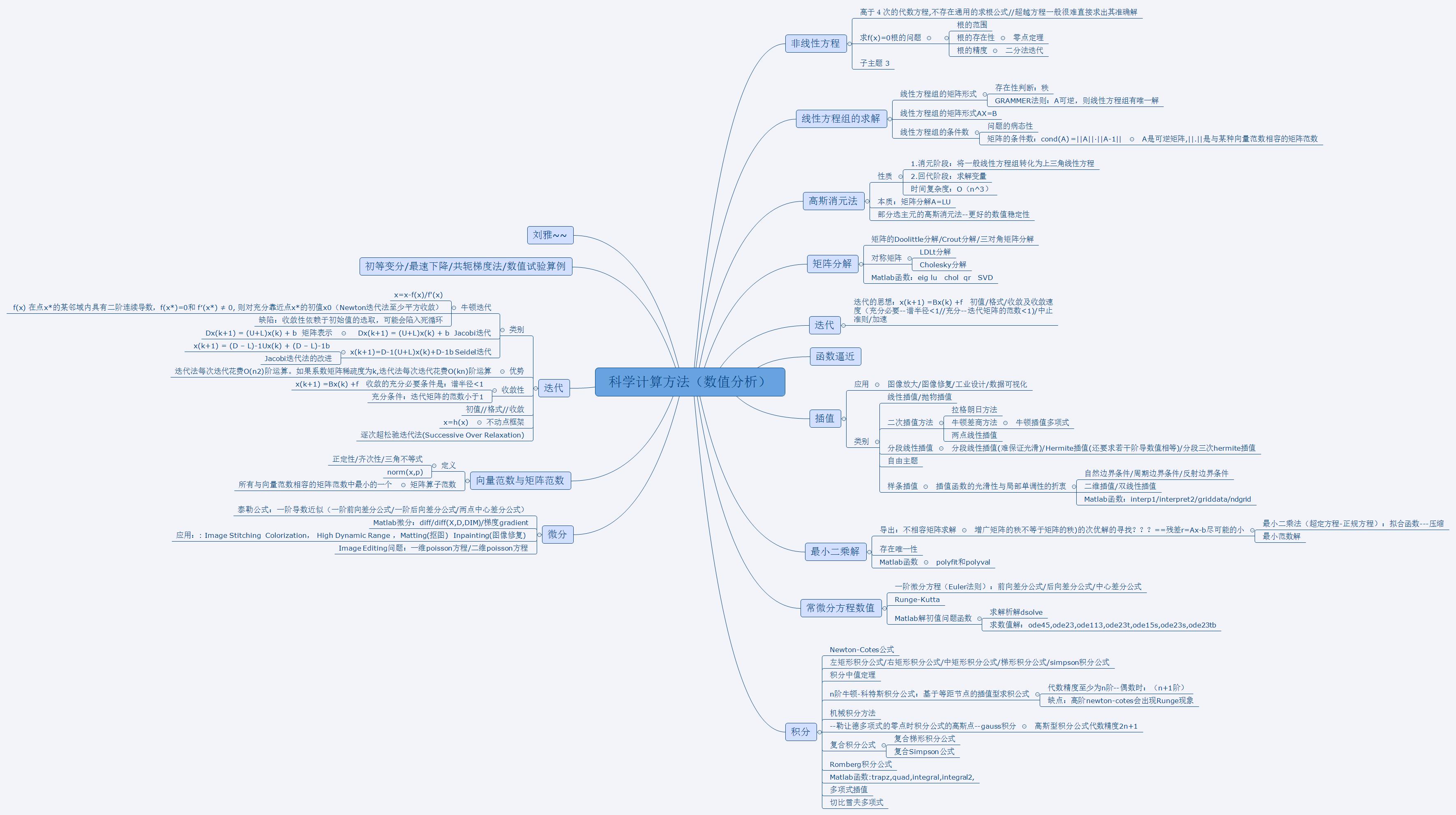
Ⅰ数值分析的基本概念

寻求数学问题（数学模型）的解是很重要的

数值型算法:迭代法，离散化技术以及离散数据的连续化技术

误差来源: 模型误差，观测误差，截断误差，舍入误差

数值计算的一些原则：1.避免绝对值较小的数字做除数         2.避免两个相近的数做加减             3.防止大数吃掉小数

---

Ⅱ 非线性方程求根方法

2.1 常识

线性方程: 指未知数都是一次的方程。

例如:一元一次方程式  二元一次方程式  ...

线性方程组：

 

代数方程与超越方程

代数函数是指只包含常数与自变量相互之间有限次的加、减、乘、除、有理指数幂和开方六种运算的函数

包含代数函数的方程为代数方程

 

以下的方程分别因为有指数函数、三角函数等超越函数，因此均为超越方程。

 

 对于超越方程，解很难求，所以常用迭代法(逐次逼近)来求。

2.2 二分法

零点定理：

设函数f(x)在闭区间[a,b]上连续，且f(a)与 f(b)异号（即f(a)× f(b)<0），那么在开区间（a,b）内至少有函数f(x)的一个零点，即至少有一点ξ（a<ξ<b）使f(ξ)=0。

 

 

2.3 迭代法

迭代法是一种逐次逼近法, 这种方法使用某个固定公式反复校正根的近似值, 使之逐步精确化, 最后得到满足精度要求的结果。

研究内容：迭代格式的构造，收敛性和收敛速度，加速收敛的技巧

 

 

 

 

 

 

 

 

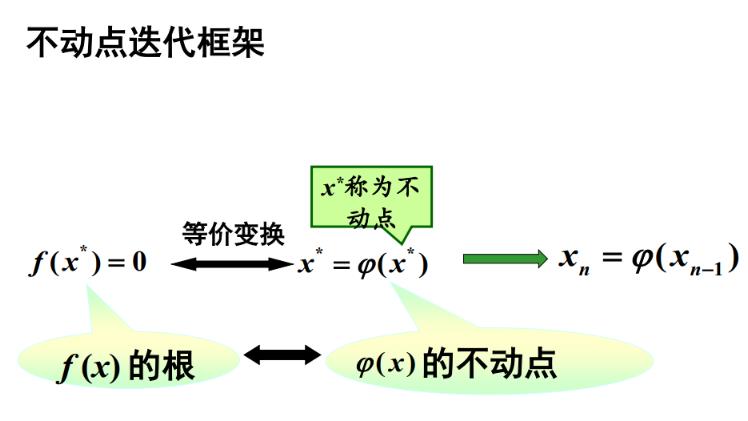
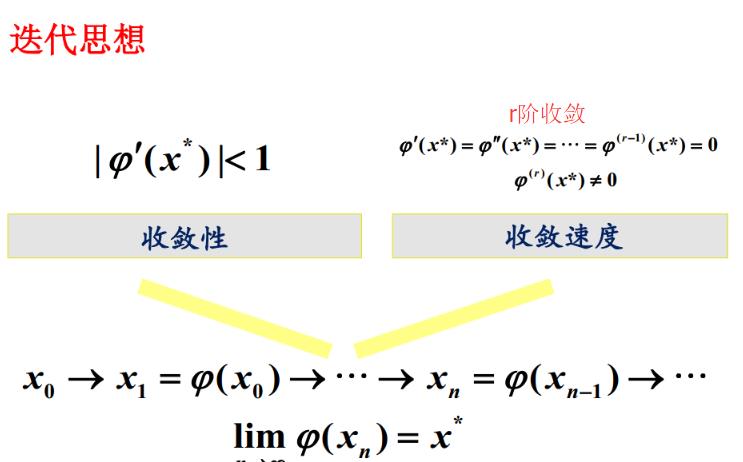
2.4 Newton迭代法

 

Ⅲ 线性方程组的直接法

数学上，“奇异”（singular）一词用来形容破坏了某种优良性质的数学对象。

对于矩阵来说，“可逆”是一个好的性质，不可逆的矩阵就称为“奇异”矩阵，而可逆阵就是非奇异矩阵

直接法：矩阵之和 （小型 / 大型稀疏阵） 第三章

迭代法：矩阵之积 （大型）                      第四章

3.1 高斯消元法及其LU三角分解

 

 

 

 

3.2 高斯列主元消元法及其LU三角分解

实际上还是3.1的高斯消元法，只是要先进行换行操作把列的主元放置在最上一行

 

 

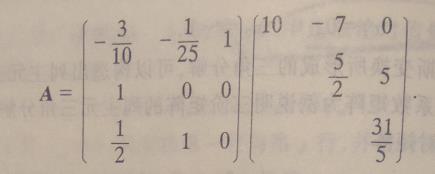
3.3 直接三角分解法

高斯消元法和列主元法都无法保证矩阵的三角分解是唯一的，因为引出直接三角分解法

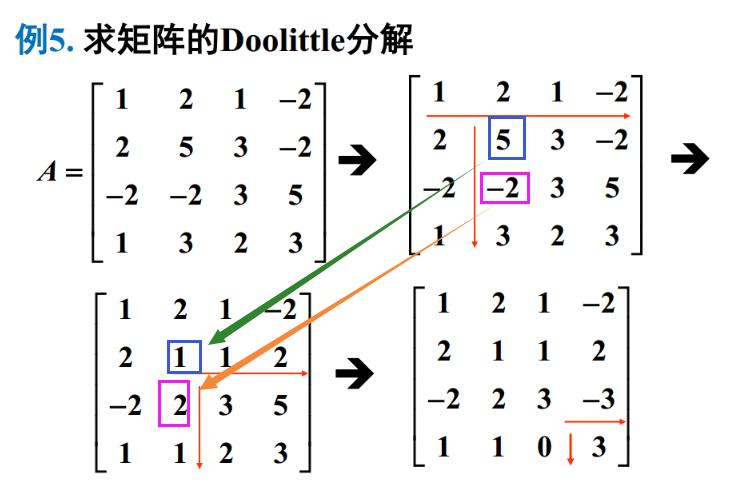
3.3.1 Doolittle分解

1先行后列，

2列除行不除，

3

5-2*2 = 1 

（-2-（-2）*2）/1=2

 

 

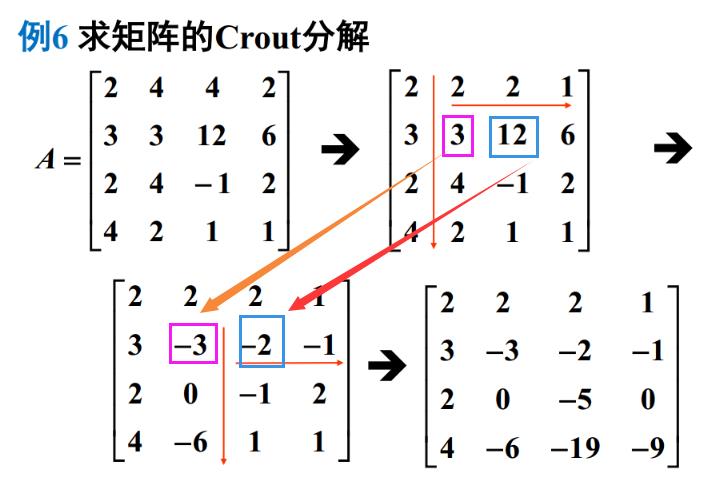
3.3.2 Crout分解

1先列后行，

2行除列不除，

3

3-2*3=-3

（12-2*3）/-3 = -2

 

 

 

3.3.3 Cholesky分解

对应成比例

 

3.3.4 范数相关

 

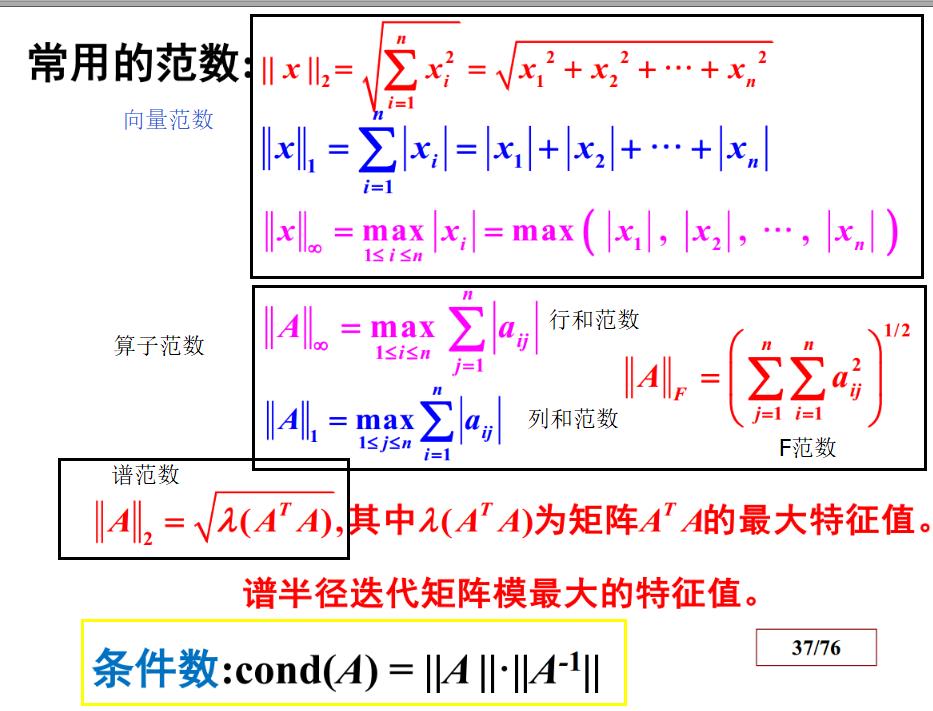
3.5 线性方程组的直接法的误差估计---条件数

对于AX=b，当输入数据A,b收到微小扰动时，可能会产生很大误差，因此需要估计近似解的误差，或者说，近似解的精确度

Cond(A)越大，则称该线性方程组是病态的，也称A是病态矩阵，反之，为良态

 

 

---

 

Ⅳ 线性方程组的迭代解法

直接法需要对系数矩阵A进行分解，因而一般不能保证A的稀疏性

引入一种可以保证矩阵稀疏性的算法：迭代法！

AX=b有唯一解X*,等价变形：

　　　　　　　　X=BX+f

 因此构造迭代格式：X^(k+1)=BX^(k)+f

若给定初始向量X(0)，则会构建一个向量序列{X^(k)}

当k->∞时候，X^(k)->X*,则

　　　　　　　　X*=BX*+f

 

则该迭代格式收敛，且B为迭代矩阵

 

4.1 Jacobi迭代

 

 

 

 

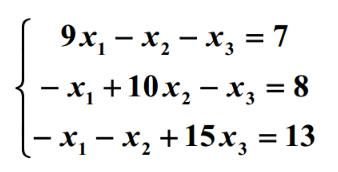
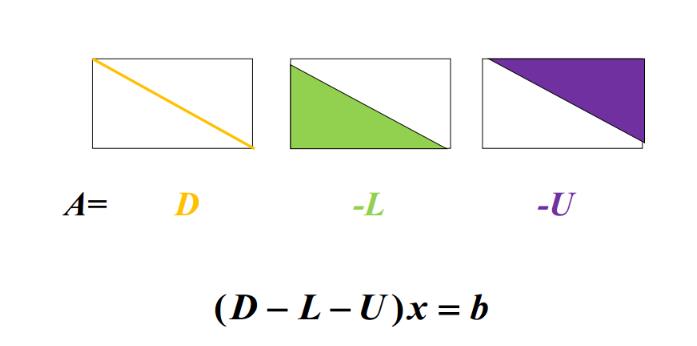
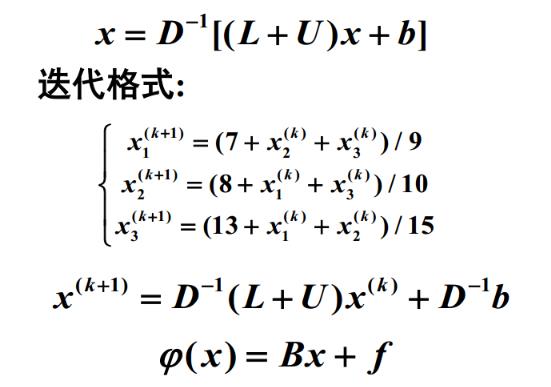
4.2 Gauss-Seidel迭代

G-S可以认为是Jacobi的一个升级版，迭代中，每算出一个新的分量，都会带入到下一次的运算中，以提升运算精度

 

 

 

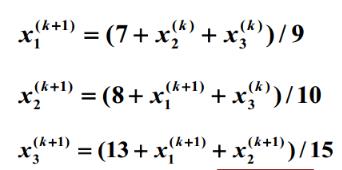
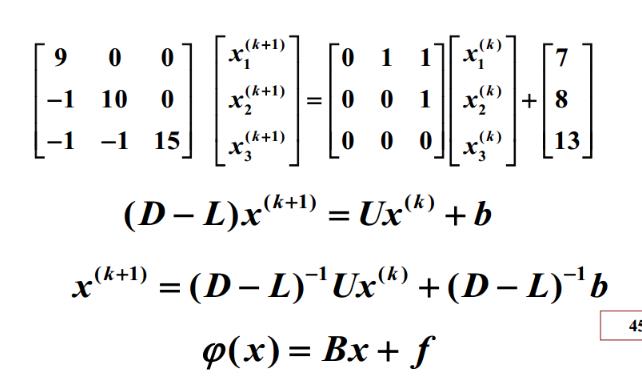
4.3 迭代法收敛的条件

 

 

4.4 超松弛(SOR)迭代法

在G-S上引入参数w构造出一种新的迭代法

w=1时候，为G-S迭代

 

 

 

 

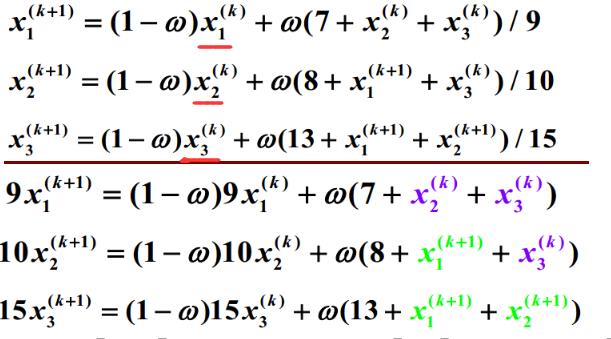
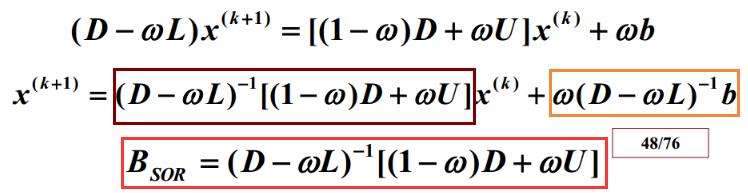
4.5 分块迭代法

 

4.6 共轭梯度算法

4.6.1 共轭向量与初等变分原理

 

 

4.6.2 最速下降法

 

4.6.3 梯度下降法

 

---

 

Ⅴ 数据插值方法---以简代繁

数据插值方法解决问题的基本目标是根据函数的离散数据构造一个简单易于计算的函数P(x)代替原有的复杂函数。可以用于根据离散数据绘制光滑曲线、图形放大算法等。

 

代数插值问题的解的存在唯一性定理

 

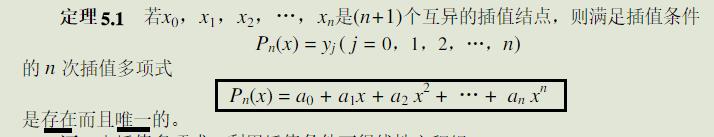
5.1 lagrange插值法

 

 

 

插值误差的大小和两个插值结点距离的平方成正比
可用于构造函数表，也可用于读一个已有的函数表时,计算表中没有的数据时做误差估计

 

 

 

5.2 牛顿插值

拉格朗日插值方法解决了插值函数的直接构造问题，以及插值误差的估计问题。但同时也使得插值函数值的计算变得复杂，

而牛顿从算法角度考虑，提出了便于计算的插值方法，这就是牛顿插值公式。 

 

 

 

5.3 分段线性插值与多元函数插值

对于区间[a，b ]上的连续函数f(x)，可以取 n+1 个插值结点计算出函数值，然后构造 n 次插值多项式Pn(x)，用以逼近f(x). 结点的数目越多则插值多项式的阶数越高。但是阶数 越高，逼近程度未必就好.

Rung反例说明，高次多项式插值可难会产生振荡现象而使插值误差很大，而分段线性插值则可以避免多项式插值的振荡现象。

5.3.1 分段线性插值

 

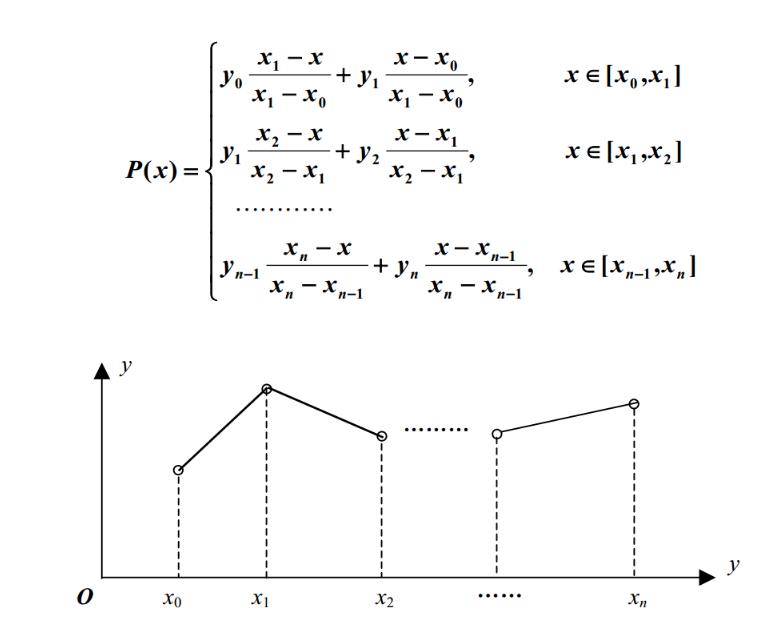
5.3.2 二元函数的双线性插值方法

 

5.4 Hermit插值

 埃尔米特（Hermite）插值方法可以处理插值条件中含导数值的插值问题。即知道插值结点处的函数值以及导数值，求插值多项式的插值问题。

 

5.5 样条插值

分段三次埃尔米特插值具有较好的光滑性，但是只有当被插值函数在插值结点处的函数值和导数值已知时才能使用。

这在实际问题中是不现实的，因为一般情况下不可能也没有必要知道函数在插值结点处的导数值。

而样条插值方法克服了分段三次埃尔米特插值的弱点，它只需要在插值区间端点比拉格朗日插值多两个边界条件，就可以构造出插值函数，而且这类插值函数在插值结点处具有二阶导数连续，从而具有更好的光滑性。

样条插值的思想来源于工程实际问题，而它的成熟的数学方法又在工程实际中得到广泛应用。

例如飞机机翼轮廓线上取有限个点，利用这些离散点的坐标绘曲线。如果用分段线性插值方法将得到折线，而用样条插值方法将绘出光滑曲线。

 

---

Ⅵ 数据拟合与函数逼近

 

 

---

 

___跋____