最大联通子数组

Posted 2020-07-05 波棱盖儿卡秃噜皮

最大联通子数组的和

 在几次“迭代”开发数组的项目之后老师又布置了这个“联通数组”的任务，当然，此次任务依旧是“结对编程”，要求如下：

1、题目：返回一个二维数整数组中最大联通子数组的和；

2、数组中有正数，也有负数；

3、求所有子数组的最大值，要求时间复杂度为O(n)；

4、程序要使用的数组放在input.txt文件中，文件的格式：行数，列数，每一行的元素；

---

 

一、实验思路 

      数组的行和列和数组元素又文件读入，然后把数按行分成几个一维数组，对于该一维数组，求出他们的最大连续数组之和，并且记录下最大连续数组的第一位和最后一位的位置，之后判断几个一维数组的最大连续数组的位置是否相接或包括。最后在加上没有包括的正数（必须在上一行的最大连续数组的第一位和最后一位的位置之间），输出之前加和。

二、实验代码及实现

代码如下：

  1 //2016/4/1 求最大联通子数组的和——赵子茵&孔宇航
  2 
  3 #include<iostream>
  4 #include<fstream>
  5 using namespace std;
  6 
  7 int Max(int n, int arr[], int *Start_mark, int *Final_mark)
  8 {
  9     int step[100] = { 0 };//Step记录每步计算子数组的和
 10     int i, sum = 0, max1 = 0;
 11     /* sum是子数组的和
 12        max1是子数组最大和
 13     */
 14     for (i = 0; i<n; i++)
 15     {
 16         if (sum<0)
 17             sum = arr[i];
 18         else
 19             sum = sum + arr[i];
 20         step[i] = sum;
 21     }
 22     max1 = step[0];
 23     for (i = 0; i<n; i++)
 24     {
 25         if (max1<step[i])
 26         {
 27             max1 = step[i];
 28             *Final_mark = i;
 29         }
 30     }
 31     for (i = *Final_mark; i >= 0; i--)
 32     {
 33         if (step[i] == arr[i])
 34         {
 35             *Start_mark = i;
 36             break;
 37         }
 38     }
 39     return max1;
 40 }
 41 
 42 void main()
 43 {
 44     int m, n, i, j, Start_mark, Final_mark, big;
 45     int Max1;
 46     int read[10000];//读取文件的字符集
 47     int up[100], down[100], h[100];
 48     int Arr2[100][100], Arr1[100];
 49     /* m行n列的数组
 50        Start_mark表示最大子数组的起始坐标
 51        Final_mark表示最大子数组的终止坐标
 52        big表示最后输出的最大联通子数组和
 53        Max1是函数返回的一维数组最大子数组和
 54        up存放每行最大子数组起始坐标
 55        down存放每行最大子数组终止坐标
 56        h存放每行最大子数组的和
 57        Arr2存放二维数组
 58        Arr1存放拆成的一维数组
 59     */
 60 
 61     /*cout << "请输入二维数组的行数和列数：";
 62     cin >> m >> n;
 63     cout << "请输入这个二维矩阵：" << endl;
 64     for (i = 0; i<m; i++)
 65     {
 66         for (j = 0; j<n; j++)
 67         {
 68             cin >> a[i][j];
 69         }
 70     }*/
 71 
 72     //文件输入
 73     ifstream infile("input.txt", ios::in);
 74     if (infile.is_open() == false)
 75     {
 76         cerr << "open error!" << endl;
 77         exit(1);
 78     }
 79     infile >> read[0];//读取行数m
 80     m = read[0];
 81     infile >> read[1];//读取列数n
 82     n = read[1];
 83     cout << "指定文件中" << read[0] << "行 " << read[1] << "列的二维数组如下：" << endl;
 84     for (i = 0; i < m; i++)//读取数组并按格式输出
 85     {
 86         for (j = 0; j < n; j++)
 87         {
 88             infile >> read[i + 2];
 89             Arr2[i][j] = read[i + 2];
 90             cout << Arr2[i][j] << " ";
 91             if (j % (n - 1) == 0 && j != 0)
 92                 //if (j == n-1)
 93                 cout << endl;
 94         }
 95     }
 96     infile.close();
 97 
 98     //把二维数组按行分解为几个一维数组
 99     for (i = 0; i<m; i++)
100     {
101         for (j = 0; j<n; j++)
102         {
103             Arr1[j] = Arr2[i][j];
104         }
105         Max1 = Max(n, Arr1, &Start_mark, &Final_mark);
106         up[i] = Start_mark;
107         down[i] = Final_mark;
108         h[i] = Max1;
109     }
110 
111     big = h[0];
112     for (i = 0; i + 1<m; i++)
113     {
114         if (up[i] <= down[i + 1] && down[i] >= up[i + 1])//联通，则相加
115             big += h[i + 1];
116         for (j = up[i]; j<up[i + 1]; j++)
117         {
118             if (Arr2[i + 1][j]>0)//是否独立正数，有则加
119                 big += Arr2[i + 1][j];     
120         }
121     }
122 
123     cout << "此二维数组的最大联通子数组的和为：" << endl;
124     cout << big << endl;
125     
126 }

运行结果如下：

      

    

     

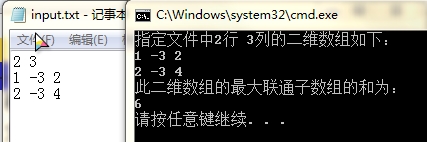
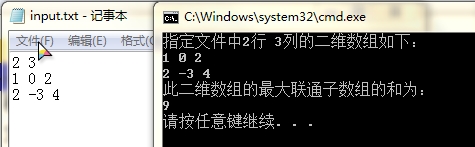
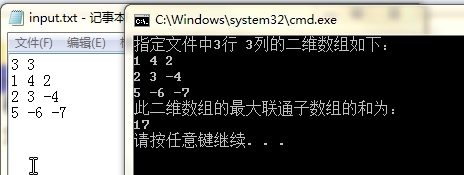
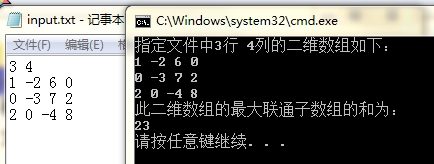
三、实验心得体会

      对于本次实验，我们最开始尝试过遍历数组的方法，设置了结构体，将数组的数设置坐标，但是后来没有掌握好方法以失败告终。在课堂上受到同学的启发将二维数组编程一位数组，比如第一行和第二行加和后出现新的一位数组的方法，在网上阅读了写别人的思路，最后和小伙伴写出了这个程序。这个程序存在缺陷，个别的测试用例会出错，现在的程序只能解决最大连续数组相连的，还不能解决不相连的，对于最后今加上剩余的正数，只会加上与第一行重合的，第三行以及以下的行并不加上前一步加上的第二行的正数。这个缺陷会在以后慢慢完善，希望老师谅解。

最后附 孔同学（孔宇航）博客地址：http://www.cnblogs.com/kongyuhang/