算法论平衡二叉树（AVL）的正确种植方法

Posted 2020-10-19 外婆的

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了算法论平衡二叉树（AVL）的正确种植方法相关的知识，希望对你有一定的参考价值。

参考资料

《算法（java）》 — — Robert Sedgewick， Kevin Wayne

《数据结构》 — — 严蔚敏

2017年度原创IT博客评选：http://www.itbang.me/goVote/203

引子

*日，为了响应市政府“全市绿化”的号召，身为共青团员的我决定在家里的后院挖坑种二叉树，以支援政府实现节能减排的伟大目标，并进一步为实现共同富裕和民族复兴打下坚实的基础....

咳咳，不好意思，扯远了。额，就是我上次不是种二叉查找树嘛（见上面的链接），发现大多数二叉树都长的比较好，但总有那么那么几颗长势很不如人意，我对此感到很疑惑（大家思考一下这是为什么）

直到—— 看门的李大爷给我送过来了一包树种，神秘兮兮地跟我说这是能自动吸收氮磷钾，犹如金坷垃般神奇的树种，它叫 —— “*衡二叉树”

正文开始

*衡二叉树的由来

普通二叉搜索树的缺陷

普通二叉搜索树的动态方法可能是“有缺陷”的，或者说：可能会带来不良的副作用

普通二叉搜索树的API分为两种： 静态方法和动态方法。

静态方法不会对二叉树做修改，而仅仅是获取相关的信息，例如：

get(根据key获取val)
max(获取最大key),
min(获取最小key)
floor（对key向下取整）
ceiling(对key向上取整)
rank（获取给定key的排名）
select（根据排名获得给定key）

而动态方法则会修改树中结点，并进一步影响二叉树的结构

put (插入键值对)
delete(删除键值对)

BST的动态方法可能会修改二叉树的结构，使其结点分布不均匀，使得在下一步的操作中，静态方法和动态方法都变得更为低效。

插入的顺序影响二叉搜索树的构造

同样的数据集合，插入二叉搜素树中的顺序的不同，树的形状和结构也是不同的

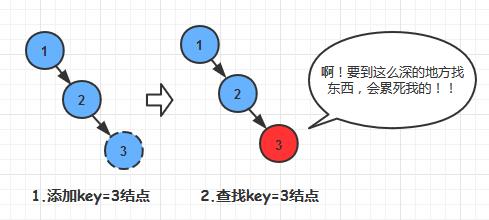
以put方法为例，我们重复调用它，用key为1, 2, 3, 4的结点构造一颗二叉搜索树。那么这颗二叉搜索树的形状取决于不同的key的插入顺序

可能在你眼里，构造的树可能是比较“均匀”的。但让我们看看， 如果按照完全正序或者逆序输入，二叉搜索树的形状就会走向一个不好的极端：

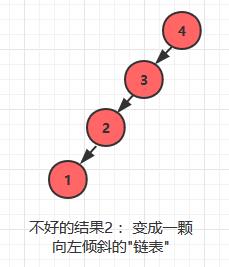
如果按照 1 -> 2 -> 3 -> 4 的顺序插入，那么这颗二叉树在形状上会变得像一颗单链表！

同样，如果按照4 -> 3 -> 2 ->1 的顺序插入，它在形状上会变成一颗向左倾斜的链表

为什么二叉搜索树会变得低效？

二叉搜索树查找的原理和二分查找类似，就是借助于它本身的结构，在遍历查找的过程中跳过一些不必要的结点的比较，从而实现高效的查找。 BST的其他API也是借助了这一优势实现性能的飞跃。但是，在这种情况下，查找一个结点将要像链表一样遍历它经过的所有结点， 二叉搜索树的高效之源已经丧失了。这就是最坏的情况。

插入和删除操作都可能降低未来操作的性能

上面我只讲述了插入操作对二叉树形状和操作性能的影响，但让我们反向思考一下就会发现，删除操作的效果也有类似之处：可能使得原来分布得比较均匀的结点，在删除部分结点之后，整体的分布变得不均匀了，并影响到未来操作的性能。

这里我先先入为主地灌输一个关于“*衡”的概念： “二叉搜索树各结点分布均匀、各种操作都较为高效的状态”

什么是*衡二叉树

综上所述，我们希望在进行动态操作（插入和删除）之后，能够通过一些指标，对二叉树的形状变化进行监督，当发现树的形状开始变得不*衡的时候，立即修正二叉树的形状。

通过这种方式， 不断地使得二叉树的形状和构造维持着一个“*衡”的状态，添加了这种维护机制的二叉搜索树，就是*衡二叉树

上个图，对比一下普通的二叉搜索树和*衡二叉树的区别：

普通的二叉搜索树（BST）

*衡二叉树（AVL）

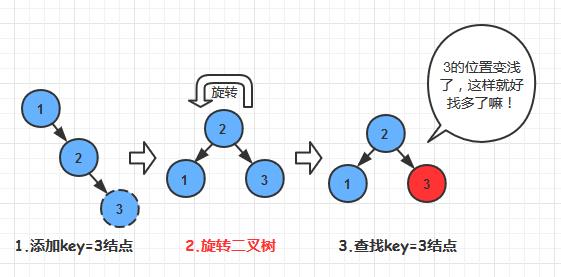
这还不够？再来个动图看一看！

（图中key的大小关系：按字母排序，A最小，Z最大）

这里我们可以很明显地看到*衡二叉树的优势所在： 使得查找的*均深度降低，优化各个API的性能开销

AVL和普通BST区别在于动态方法

*衡二叉树和普通二叉查找树区别主要在于动态方法！(put,delete) 。它们的静态方法基本是相同的！（get,min,max,floor,ceiling, rank,select）

所以本文编写的主要API就只有两个: put和delete

*衡二叉树的监督机制

我们前面提到了*衡二叉树有它的监督机制，既然说到“监督”，那必然就有一个用于判断当前二叉树*不*衡的指标，这个监督的指标，就是*衡因子（Balance Factor）。

在二叉树中，我们为每个结点定义了*衡因子这个属性。

*衡因子：某个结点的左子树的高度减去右子树的高度得到的差值。

*衡二叉树（AVL）：所有结点的*衡因子的绝对值都不超过1。即对*衡二叉树每个结点来说，其左子树的高度 - 右子树高度得到的差值只能为 1， 0 ， -1 这三个值。取得小于 -1或者大于1的值，都被视为打破了二叉树的*衡

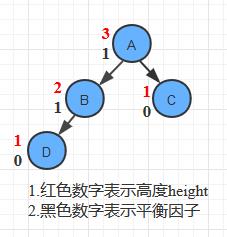
图解*衡因子

下图中：

对根结点A而言，它左子树高度为2，右子树高度为1，那么它的*衡因子BF = 2 - 1 = 1

对结点B而言，它左子树高度为1，没有右子树（高度视为0），BF = 1 - 0 = 1；

图解*衡二叉树

如下图所示，图a的两颗是*衡二叉树，图b的两颗则是非*衡二叉树

所以，只有所有结点都符合“*衡因子的绝对值都不超过1” 这一条件的二叉树，才是*衡二叉树；

如果有一个结点不符合条件，那么这颗二叉树就不是*衡二叉树。

上面我们说到，在动态操作（插入/删除）的过程中，我们需要*衡因子作为“指标”，去监督当前这颗二叉树的构造是否符合预期，即——是否是一颗*衡二叉树。

而*衡因子BF的计算需要用到该节点的孩子结点的高度属性，这也就意味着，我们要从Node类的实例变量入手，为每个结点设置height属性，并在二叉树结构发生变化时，更新并维护height的正确性。

为每个结点设置并维护height属性

height属性的设置

啊，终于可以开始写代码了。如下，我们在Node类中写入了实例变量height,并初始化为1

/**
 * @Author: HuWan Peng
 * @Date Created in 10:35 2017/12/29
 */
public class AVL {
  Node root; // 根结点
  private class Node {
    int key,val;
    Node left,right;
    int height = 1; // 每个结点的高度属性
    public Node (int key, int val) {
      this.key = key;
      this.val = val;
    }
  }
  // 编写API方法
}

height属性的维护和更新

让我们思考一下， 结点height属性在什么时候会发生变化： 当然是在二叉树结构发生变化的时候，具体表现为：

在插入结点时（put），沿插入的路径更新结点的高度值（不一定会加1 ！只是要重新计算）
在删除结点时（delete）,沿删除的路径更新结点的高度值（不一定减1！只是要重新计算）
在发现二叉树变得不*衡的时候，通过“旋转”使其*衡，这时候要更新相关结点的高度值（具体的我下面会详细讲）

下面的代码是更新结点高度的示范例子：

  /**
   * @description: 返回两个数中的最大值
   */
  private int max (int a, int b) {
    return a>b ? a : b;
  }
 
  /**
   * @description: 获得当前结点的高度
   */
  private int height (Node x) {
    if(x == null) return 0;
    return x.height;
  }
 
  // 下面的insert方法是简化后的代码
  public Node insert (Node x, int key, int val) {
    其他代码 。。。。
    insert(x.left, key, val); // 进行递归的插入
    x.height = max(height(x.left),height(x.right)) + 1; // 更新结点的height属性（沿着递归路径）
    return x;
  }

最关键的是

  x.height = max(height(x.left),height(x.right)) + 1;

这一句代码，因为在递归的插入或删除之后，沿着递归路径上方的结点的height都有可能会改变， 所以要通过依次调用这一段代码，沿着递归路径自下而上地更新沿途结点的height属性值。

计算BF以监督*衡二叉树的状态

只要我们能正确地维护每个结点的height，我们就能对动态操作中受影响的结点，准确计算其*衡因子（BF），从而判断当前的*衡二叉树的状态

计算某个结点*衡因子的方法：

  /**
   * @description: 获得*衡因子
   */
  private int getBalance (Node x) {
    if(x == null) return 0;
    return height(x.left) - height(x.right);
  }

*衡二叉树的修正机制

当我们计算出某个结点的*衡因子的绝对值超过1时，我们就要对其进行修正，即通过*衡化的处理，使得不*衡的二叉树重新变得*衡。

左旋和右旋

二叉树的*衡化有两大基础操作：左旋和右旋

1. 左旋，即是逆时针旋转；右旋，即是顺时针旋转

2. 这种旋转在整个*衡化过程中可能进行一次或多次

3.且是从失去*衡的最小子树根结点开始的(即离插入结点最*的、*衡因子超过1的祖先结点)

右旋操作

右旋操作过程：使结点3位置“下沉”，而结点2位置“上浮”，反转当前结点和它左儿子的父子关系。

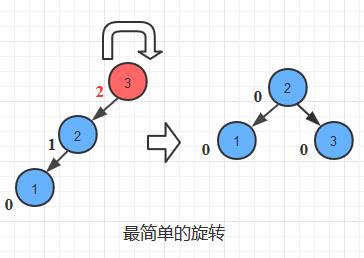
但是，让我们思考地再全面一些：如果上图中的结点2有右儿子的话，情况会变得怎样？

这时候结点2将保持有3条链接，如果在这种情况下旋转，结点二需要抛弃一条链接。

我们的处理方式是： 抛弃结点2的右儿子，将其和旋转后的结点3连接，成为结点3的左儿子

我将上面的这种假设的结点戏称为“拖油瓶”结点， 如下图中的黄色结点

紧接上图，我们需要先断开4结点和3结点间的链接，然后把它转接到旋转后的结点5上：

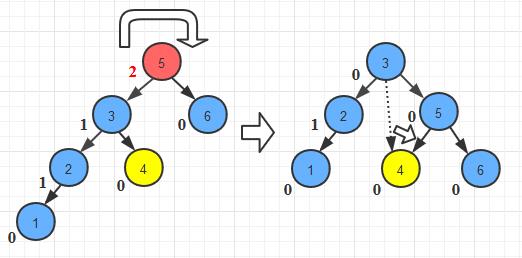
当然，有的时候我们假设的这个“拖油瓶”结点（黄色结点）可能是空的，但是这并不影响我们的编码。

好嘞！让我们来编写右旋的代码：

  /**
   * @description: 右旋方法
   */
  private Node rotateRight (Node x) {
    Node y = x.left; // 取得x的左儿子
    x.left = y.right; // 将x左儿子的右儿子（"拖油瓶"结点）链接到旋转后的x的左链接中
    y.right = x; // 调转x和它左儿子的父子关系，使x成为它原左儿子的右子树
    x.height = max(height(x.left),height(x.right)) + 1; // 更新并维护受影响结点的height
    y.height = max(height(y.left),height(y.right)) + 1; // 更新并维护受影响结点的height
    return y; // 将y返回
  }

左旋操作

左旋操作的过程和右旋一样：

例如下面：

1. 结点2位置“下沉”，而结点4位置上浮，反转当前结点和它右儿子的父子关系（2和4），使2结点变成4结点的左儿子。

2. 同时断裂结点3和结点4间的链接，转接到结点2中（处理拖油瓶结点）

左旋方法代码如下：

  /**
   * @description: 左旋方法
   */
  private  Node rotateLeft (Node x) {
    Node y = x.right;  // 取得x的右儿子
    x.right = y.left; // 将x右儿子的左儿子（"拖油瓶"结点）链接到旋转后的x的右链接中
    y.left = x; // 调转x和它右儿子的父子关系，使x成为它原右儿子的左子树
    x.height = max(height(x.left),height(x.right)) + 1; // 更新并维护受影响结点的height
    y.height = max(height(y.left),height(y.right)) + 1; // 更新并维护受影响结点的height
    return y; // 将y返回
  }

*衡化操作的四种情况

以左旋操作和右旋操作为基础，构成了*衡化操作的四种情况

假设由于在二叉排序树上插入结点而失去*衡的最小子树的根结点为a (即a是离插入结点最*的、*衡因子超过1的祖先结点)，则失去*衡后的调整操作分为以下4种情况:

1. 单次右旋： 由于在a的左子树的根结点的左子树上插入结点（LL），使a的*衡因子由1变成2，导致以a为根的子树失去*衡，则需进行一次的向右的顺时针旋转操作

2. 单次左旋： 由于在a的右子树根结点的右子树上插入结点（RR），a的*衡因子由-1变成-2，导致以a为根结点的子树失去*衡，则需要进行一次向左的逆时针旋转操作

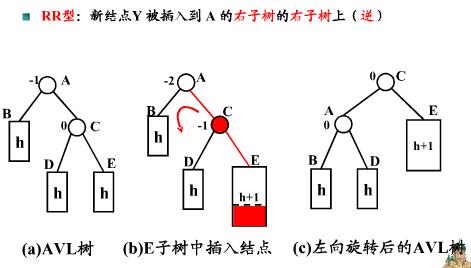
3. 两次旋转、先左旋后右旋： 由于在a的左子树根结点的右子树上插入结点（LR），导致a的*衡因子由1变成2，导致以a为根结点的子树失去*衡，需要进行两次旋转，先左旋后右旋

4.两次旋转，先右旋后左旋： 由于在a的右子树根结点的左子树上插入结点（RL）， a的*衡因子由-1变成-2，导致以a为根结点的子树失去*衡，则需要进行两次旋转，先右旋后左旋

那么问题来了，怎么分别判断LL， RR，LR，RL这四种破环*衡的场景呢？

我们可以根据当前破坏*衡的结点的*衡因子，以及其孩子结点的*衡因子来判断，具体如下图所示：

（BF表示*衡因子，最下方的那个结点是新插入的结点）

编写*衡化代码

有了以上的知识基础，让我们来编写下我们的*衡化代码

  /**
   * @description: 获得*衡因子
   */
  private int getBalance (Node x) {
    if(x == null) return 0;
    return height(x.left) - height(x.right);
  }
  /**
   * @description: *衡化操作：  检测当前结点是否失衡，若失衡则进行*衡化
   */
  private Node reBalance (Node x) {
    int balanceFactor = getBalance(x);
    if(balanceFactor > 1&&getBalance(x.left)>0) { // LL型，进行单次右旋
     return rotateRight(x);
    }
    if(balanceFactor > 1&&getBalance(x.left)<=0) { //LR型 先左旋再右旋
      Node t = rotateLeft(x);
      return rotateRight(t);
    }
    if(balanceFactor < -1&&getBalance(x.right)<=0) {//RR型， 进行单次左旋
      return rotateLeft(x);
    }
    if(balanceFactor < -1&&getBalance(x.right)>0) {// RL型，先右旋再左旋
      Node t = rotateRight(x);
      return rotateLeft(t);
    }
    return x;
  }

AVL类的API编码

下面我将展示*衡二叉树的put方法和delete方法的代码，而这两个方法绝大部分的代码还是基于二叉查找树的put方法和delete方法的，所以还不太了解BST的同学可以看一看我上篇文章对BSTput方法和delete方法的解析：

【算法】二叉查找树（BST）实现字典API

插入方法

在看代码前可以先看下对二叉查找树中put方法的解析

二叉查找树的put方法

*衡查找树的put方法

  /**
   * @description: 插入结点（键值对）
   */
  public Node put (Node x, int key, int val) {
    if(x == null) return new Node(key, val); // 插入键值对
    if     (key<x.key) x.left  = put(x.left, key, val); // 向左子树递归插入
    else if(key>x.key) x.right = put(x.right,key, val); // 向右子树递归插入
    else x.val = val; // key已存在， 替换val
    x.height = max(height(x.left),height(x.right)) + 1; // 沿递归路径从下至上更新结点height属性
    x = reBalance(x); // 沿递归路径从下往上, 检测当前结点是否失衡，若失衡则进行*衡化
    return x;
  }

删除方法

删除方法比较复杂，在看代码前可以先看下对二叉查找树中put方法的解析

二叉查找树的delete方法

*衡查找树的delete方法

  /**
   * @description: 返回最小键
   */
  private Node min (Node x) {
    if(x.left == null) return x; // 如果左儿子为空，则当前结点键为最小值，返回
    return min(x.left);  // 如果左儿子不为空，则继续向左递归
  }
  public int min () {
    if(root == null) return -1;
    return min(root).key;
  }
 
  /**
   * @description: 删除最小键的结点
   */
  public Node deleteMin (Node x) {
    if(x.left==null) return x.right; // 如果当前结点左儿子空，则将右儿子返回给上一层递归的x.left
    x.left = deleteMin(x.left);// 向左子树递归， 同时重置搜索路径上每个父结点指向左儿子的链接
    return x; // 当前结点不是min
  }
  public void deleteMin () {
    root = deleteMin(root);
  }
 
  /**
   * @description: 删除给定key的键值对
   */
  private Node delete (int key,Node x) {
    if(x == null) return null;
    if      (key<x.key) x.left  = delete(key,x.left); // 向左子树查找键为key的结点
    else if (key>x.key) x.right = delete(key,x.right); // 向右子树查找键为key的结点
    else{
      // 结点已经被找到，就是当前的x
      if(x.left==null) return x.right; // 如果左子树为空，则将右子树赋给父节点的链接
      if(x.right==null) return x.left; // 如果右子树为空，则将左子树赋给父节点的链接
      Node inherit = min(x.right); // 取得结点x的继承结点
      inherit.right = deleteMin(x.right); // 将继承结点从原来位置删除，并重置继承结点右链接
      inherit.left = x.left; // 重置继承结点左链接
      x = inherit; // 将x替换为继承结点
    }
    if(root == null) return root;
    x.height = max(height(x.left),height(x.right)) + 1; // 沿递归路径从下至上更新结点height属性
    x = reBalance(x); // 沿递归路径从下往上, 检测当前结点是否失衡，若失衡则进行*衡化
    return x;
  }
  public void delete (int key) {
    root = delete(key, root);
  }

测试AVL和BST的动态操作对二叉树结构的影响

下面我们用层序遍历的方式进行测试：

  /**
   * @description: 二叉树层序遍历
   */
  private void levelIterator () {
    LinkedList <Node> queue = new LinkedList <Node>();
    Node current = null;
    int childSize = 0;
    int parentSize = 1;
    queue.offer(root);
    while(!queue.isEmpty()) {
      current = queue.poll();//出队队头元素并访问
      System.out.print(current.val +" ");
      if(current.left != null)//如果当前节点的左节点不为空入队
      {
        queue.offer(current.left);
        childSize++;
      }
      if(current.right != null)//如果当前节点的右节点不为空，把右节点入队
      {
        queue.offer(current.right);
        childSize++;
      }
      parentSize--;
      if (parentSize == 0)
      {
        parentSize = childSize;
        childSize = 0;
        System.out.println("");
      }
    }
  }

测试普通BST

  public static void main(String [] args) {
    BST bst = new BST();
    bst.put(1,11);
    bst.put(2,22);
    bst.put(3,33);
    bst.put(4,44);
    bst.put(5,55);
    bst.put(6,66);
    bst.levelIterator();
  }

输出：

(6层！！！)

测试AVL：

  public static void main (String [] args) {
    AVL avl = new AVL();
    avl.put(1,11);
    avl.put(2,22);
    avl.put(3,33);
    avl.put(4,44);
    avl.put(5,55);
    avl.put(6,66);
    avl.levelIterator();
  }

输出：

(只有3层！)

44
22 55
11 33 66

全部代码

import java.util.LinkedList;
 
/**
* @Author: HuWan Peng
* @Date Created in 10:35 2017/12/29
*/
以上是关于算法论平衡二叉树（AVL）的正确种植方法的主要内容，如果未能解决你的问题，请参考以下文章 
 数据结构&算法-AVL平衡二叉树
 数据结构&算法-AVL平衡二叉树
 D13-平衡二叉树[Java数据结构和算法]
 平衡二叉树的介绍
 平衡二叉树之AVL树
 算法小讲堂之平衡二叉树|AVL树（超详细~）