算法小讲堂之平衡二叉树|AVL树（超详细~）

Posted 2022-09-02 MangataTS

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了算法小讲堂之平衡二叉树|AVL树（超详细~）相关的知识，希望对你有一定的参考价值。

文章目录

一、前言

通过前面的二叉排序树的学习（传送门：https://acmer.blog.csdn.net/article/details/126607632），我们发现了一个问题，如果说数据的插入顺序是一个有序的，那么这个二叉排序树就会退化成链状，这就导致了二叉排序树的查找速度直接变为 $O (N)$ 那这就和线性表没啥区别了，有没有什么办法能让这个二叉树最好一直稳定在 “最佳状态”呢 那么就要引出今天的主角： 平衡树（AVL树） 了，其实 $A V L$ 树的原理非常简单，在正常二叉排序树的操作中只是多加入了四种旋转子树的操作使得这颗二叉树的高度尽量保持平衡（即不让树的高度增长过快）

二、定义

平衡二叉树，又称 $A V L$ 树，它是一种 特殊的 二叉排序树。AVL树或者是一棵空树，或者是具有以下性质的二叉树：

左右子树都是一颗平衡树
左子树和右子树的深度（高度）之差的绝对值不超过 $1$

对于每一个分支节点，左右子树的高度差就为该节点的 平衡因子 ，显然对于每一个叶结点高度差为 $0$ ，例如下图两颗分别为平衡和非平衡树：

其中结点的值就是该结点的 平衡因子

三、原理

首先是对于二叉树的结点定义，对于这个结点我们需要比之前的二叉排序树多一个值就是 height 用于记录当前结点的高度，所以得到结点的定义如下：

template<typename T>
class AvlNode 
public:
    T key;
    int height;
    AvlNode *left,*right;
    AvlNode(int key) 
        this->key = key;
        this->height = 0;
        this->left = this->right = NULL;
    
    ~AvlNode() 

    
;

然后我们再抽象一个树的定义，即一个包含树的根节点，以及树的操作函数的类：

template<typename T>
class AvlTree 
public:

    AvlNode<T> *root;

    AvlTree() 
        this->root = NULL;
    

    //获取树结点的高度
    int GetHeight(AvlNode<T> *root);

    //更新树结点的高度
    int MaxHeight(AvlNode<T> *root);

    //判断是否失去平衡，失去平衡返回true，否则返回false
    bool Check_Balance(AvlNode<T> *a, AvlNode<T> *b);

    //简称为LL旋转（LL的含义是左子树的左子树插入新结点）
    AvlNode<T>* LeftLeftRotate(AvlNode<T> *root);

    //简称为RR旋转（RR的含义是右子树的右子树插入新结点）
    AvlNode<T>* RightRightRotate(AvlNode<T> *root);

    //简称为LR旋转（LR的含义是左子树的右子树插入新节点）
    AvlNode<T>* LeftRightRotate(AvlNode<T> *root);

    //简称为RL旋转（RL的含义是右子树的左子树插入新节点）
    AvlNode<T>* RightLeftRotate(AvlNode<T> *root);

    //在AVL树中查找元素值为value的结点
    AvlNode<T>* ValueFind(AvlNode<T> *root,T value);

    //找到AVL树中元素值最小的结点，即树的最左边
    AvlNode<T>* MinNode(AvlNode<T> *root);

    //找到AVL树中元素值最大的结点，即树的最右边
    AvlNode<T>* MaxNode(AvlNode<T> *root);

    //在AVL树中插入元素值为T的结点
    AvlNode<T>* InsetNode(AvlNode<T> *root,T value);

    //删除结点
    AvlNode<T>* DeleteNode(AvlNode<T> *root, AvlNode<T> *node);

    //先序遍历
    void PreOrder(AvlNode<T> *root) 
        if(root == NULL) return;
        std::cout<<root->key<<"->";
        PreOrder(root->left);
        PreOrder(root->right);
    
    //中序遍历
    void InOrder(AvlNode<T> *root) 
        if(root == NULL) return;
        InOrder(root->left);
        std::cout<<root->key<<"->";
        InOrder(root->right);
    
    //后序遍历
    void PostOrder(AvlNode<T> *root) 
        if(root == NULL) return;
        PostOrder(root->left);
        PostOrder(root->right);
        std::cout<<root->key<<"->";
    
;

其中三种遍历方式是为了后面校验平衡二叉树的形态是否正确，前三个函数：

int GetHeight(AvlNode<T> *root) ：传入一个二叉树的结点，然后我们返回这个二叉树结点的height成员变量，但是我们传入的结点可能是 NULL 直接去取元素的话会发生 RE 所以我们需要先判断一下
int MaxHeight(AvlNode<T> *root); ：其实叫UpdataHeight更为合理，是用于更新当前结点的高度的函数
bool Check_Balance(AvlNode<T> *a, AvlNode<T> *b);：传入两个结点，判断一下以他们分别作为根结点的子树的高度是否发生失衡，如果失衡那么就返回 true 否则返回 false

3.1 查找操作

前面说了只有树形结构发生变化的时候才会导致二叉树失去平衡，那么显然只有是插入和删除结点的操作的时候才可能发生，所以对于查找的操作来说和前面的平衡二叉树是相同的，代码如下：

template<typename T>
AvlNode<T>* AvlTree<T>::ValueFind(AvlNode<T> *root,T value) 
    //如果当前走到了空结点或者找到了value值的结点都会退出，前者说明找不到
    while(root != NULL && root->key != value) 了，后者说明找到了
        if(root->key > value) 
        	root = root->left;//在左子树
        else 
        	root = root->right;//在右子树
    
    return root;//没找到的话会返回NULL

3.2 最小（大）值结点

最大值结点就是在整棵树的最右边，也就是从根节点出发一直往右子树走，直到某个结点的右儿子为NULL 此时就找到了，代码如下：

template<typename T>
AvlNode<T>* AvlTree<T>::MaxNode(AvlNode<T> *root) 
    if(root == NULL) //特判一下空树的情况
        return NULL;
    if(root->right == NULL) //当结点的右子树为空，说明找到了
        return root;
    return MaxNode(root->right);//递归往右子树查找

最小值结点和最大值同理，从根节点出发一直往左子树走，直到某个结点的左儿子为 NULL，此时就找到了，代码如下：

template<typename T>
AvlNode<T>* AvlTree<T>::MinNode(AvlNode<T> *root) 
    if(root == NULL) 
        return NULL;//特判一下空树的情况
    if(root->left == NULL) //当结点的左子树为空，说明找到了
        return root;
    return MinNode(root->left);

3.3 旋转操作

平衡二叉树最重要最核心的操作也就是旋转操作了，总体分为四种旋转操作，即 $LL$ 旋转、 $RR$ 旋转、 $L R$ 旋转、 $R L$ 旋转，这里的定义其实是很有关系的，我们一一来讲解，先放两张失衡 $A V L$ 树的图，结合下面的定义以及实现观看：
case1:

case2:

3.3.1 LL旋转

发生情况：
这里的 LL 指的是指通过在最低失去平衡的结点的左子树的左子树插入结点，导致失衡所要做出的旋转，当然若是失衡结点的右子树结点被删除也有可能造成LL旋转，因为就等同左子树的左子树插入结点
操作：
当发生 LL 失衡的时候，我们可以简单将这颗 $A V L$ 抽象成如下图所示：

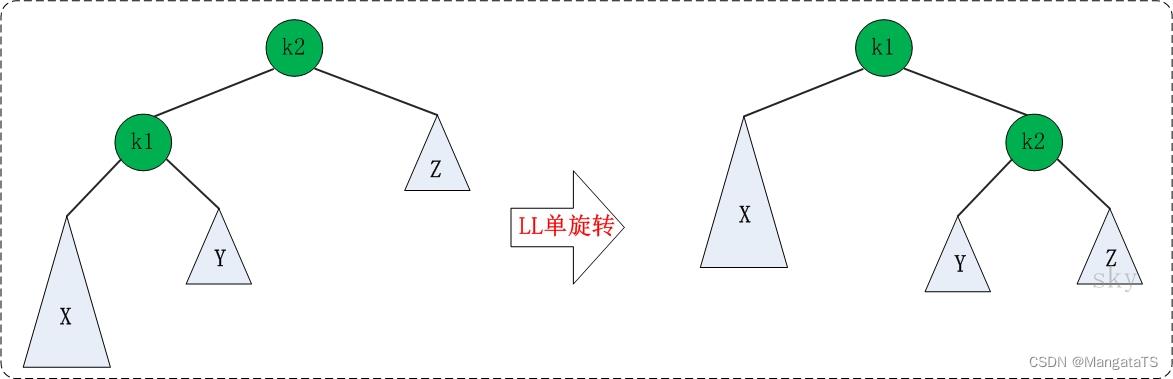
可以简单分为四步：
将左子树的右子树（Y）变为根（K2）的左子树
将左子树的根结点 $k 1$ 变为整个子树的根结点，然后让其右子树指针指向之前的根 $k 2$
更新 $k 1$ 和 $k 2$ 的高度
将旋转后的新根（ $k 1$ ）返回

比如插入序列为： $\\5,6,3,2,4,1 \\$ 的时候，此时以 $5$ 为根节点的位置的左子树发生了失衡，然后我们对其进行LL旋转将左儿子结点旋转到根节点的位置，如下图所示：

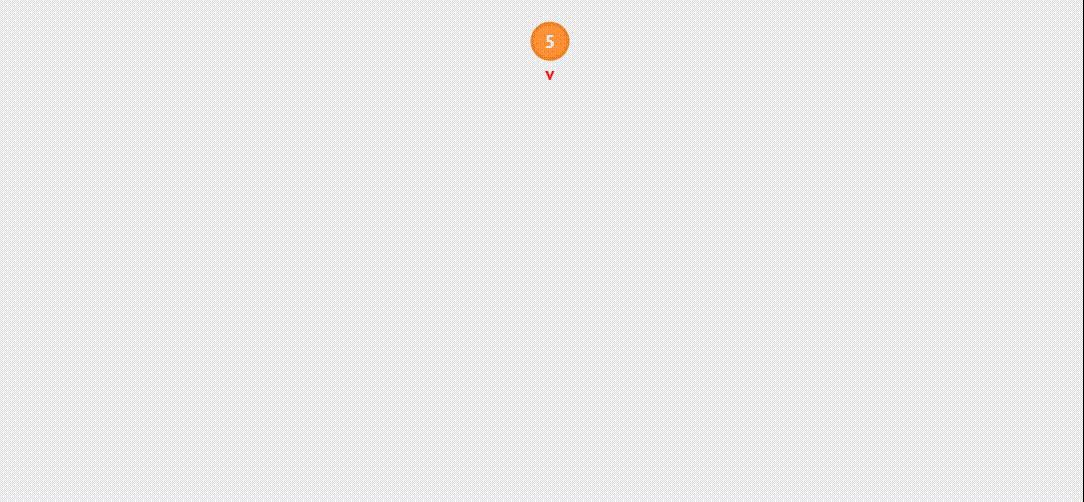
步骤明白后，代码其实也就很简单了：

template<typename T>
AvlNode<T>* AvlTree<T>::LeftLeftRotate(AvlNode<T> *root) 
    AvlNode<T> *lchild = root->left;//记录一下左子树根结点
    root->left = lchild->right;//将左子树的右子树变为根的左子树
    lchild->right = root;//将左子树的根变为整个树的根，然后让其右子树指向之前的根

    //更新一下当前子树的根结点的高height
    lchild->height = MaxHeight(lchild);
    //更新一下被旋下去的结点，即当前子树的根的右子树结点的高height
    root->height = MaxHeight(root);

    return lchild;//返回子树旋转后的新的根

实际上我们说对某一个结点做LL旋的话，其实就是想将那个结点 往右旋转

3.3.2 RR旋转

发生情况：
这里的 RR 指的是指通过在最低失去平衡的结点的右子树的右子树插入结点，导致失衡所要做出的旋转，当然若是失衡结点的左子树结点被删除也有可能造成RR旋转，因为就“等同右子树的右子树插入结点”
操作：
当发生 RR 失衡的时候，我们可以简单将这颗 $A V L$ 抽象成如下图所示：

其实你会发现 $RR$ 单旋转是和前面的 $LL$ 单旋转其实是对称的，那么操作步骤仍然是四步：
①将右子树的左子树（Y）变为根（K1）的左子树
②将左子树的根结点 $k 2$ 变为整个子树的根结点，然后让其左子树指针指向之前的根 $k 1$
③更新 $k 1$ 和 $k 2$ 的高度
④将旋转后的新根（ $k 2$ ）返回

比如插入序列为： $\\2,1,4,5,3,6 \\$ 的时候，此时以 $2$ 为根节点的位置的右子树发生了失衡，然后我们对其进行RR旋转将右儿子结点旋转到根节点的位置，如下图所示：

代码如下：

template<typename T>
AvlNode<T>* AvlTree<T>::RightRightRotate(AvlNode<T> *root) 
    AvlNode<T> *rchild = root->right;//记录一下右子树根结点
    root->right = rchild->left;//将右子树的左子树变为根的右子树
    rchild->left = root;//将右子树的根变为整个树的根，然后让其右子树指向之前的根
	//结点高度更新操作
    rchild->height = MaxHeight(rchild);
    root->height = MaxHeight(root);
	//返回新的根
    return rchild;

实际上我们说对某一个结点做RR旋的话，其实就是想将那个结点 往左旋转

3.3.3 LR旋转

发生情况：
这里的 LR 指的是指通过在最低失去平衡的结点的左子树的右子树插入结点，导致失衡所要做出的旋转，当然若是失衡结点的右子树结点被删除也有可能造成LR旋转，因为就“等同左子树的右子树插入结点”
操作：
当发生 LR 失衡的时候，我们可以简单将这颗 $A V L$ 抽象成如下图所示：

我们需要做一次 RR 单旋转以及一次 LL 单旋，对于上面的情况，我们需要先对 $k 1$ 结点做一次 RR 单旋，然后再对 $k 3$ 做一次 LL 单旋，这样就能让二叉树重归平衡

那么步骤的话就可以简化为三步啦（因为之前实现了简单的结点LL右旋和RR左旋操作）

①将失衡结点（ $k 3$ ）的左子树结点（ $k 1$ ）RR左旋
②将失衡结点（ $k 3$ ）LL右旋
③将新的根节点（ $k 2$ ）返回

比如插入序列为： $\\6,7,2,1,4,3,5 \\$ 的时候，此时以 $6$ 为根节点的位置的左子树发生了失衡，然后我们对以 $2$ 为根的左子树进行 RR左旋转然后再对根结点 $6$ 进行 LL 右旋如下图所示：

实现代码如下：

template<typename T>
AvlNode<T>* AvlTree<T>::LeftRightRotate(AvlNode<T> *root) 
    root->left = RightRightRotate(root->left);//先对左子树进行进行RR旋转
    root = LeftLeftRotate(root);//然后对根节点进行LL旋转
    return root;//返回新的根

3.3.4 RL旋转

发生情况：
这里的 RL 指的是指通过在最低失去平衡的结点的右子树的左子树插入结点，导致失衡所要做出的旋转，当然若是失衡结点的左子树结点被删除也有可能造成LR旋转，因为就“等同右子树的左子树插入结点”
操作：
当发生 RL 失衡的时候，我们可以简单将这颗 $A V L$ 抽象成如下图所示：

我们需要做一次 LL 单旋转以及一次 RR 单旋，对于上面的情况，我们需要先对 $k 3$ 结点做一次 LL 单旋，然后再对 $k 1$ 做一次 RR 单旋，这样就能让二叉树重归平衡

那么步骤的话同样分为三步啦（因为之前实现了简单的结点LL右旋和RR左旋操作）

①将失衡结点（ $k 1$ ）的右子树结点（ $k 3$ ）LL 右旋
②将失衡结点（ $k 1$ ）LL左旋
③将新的根节点（ $k 2$ ）返回

比如插入序列为： $\\2,1,6,7,4,3,5 \\$ 的时候，此时以 $2$ 为根节点的位置的右子树发生了失衡，然后我们对以 $6$ 为根的右子树进行 LL右旋转然后再对根结点 $2$ 进行 RR 左旋如下图所示：

代码如下：

template<typename T>
AvlNode<T>* AvlTree<T>什么是平衡二叉树
 平衡二叉树（AVL树）
 图解数据结构树之AVL树
 树结构实际应用之平衡二叉树(AVL 树)
 平衡二叉树(AVL树)
 数据结构之二叉树扩展AVL,B-,B+,红黑树