线段树

Posted 2020-10-19 wangguodong

线段树是经常使用完全二叉树来实现，也就是使用一个数组来表示（0号元素通常不做使用）。线段树的叶子节点存储的是实际的数据，而非叶子节点存储的是该节点对应区间的信息（比如该区间的最值，求和等）。举例说明，假如非叶子节点存储区间的最小值，数据为[2,5,1,4,9,3]，则可以构造出的线段树如下：

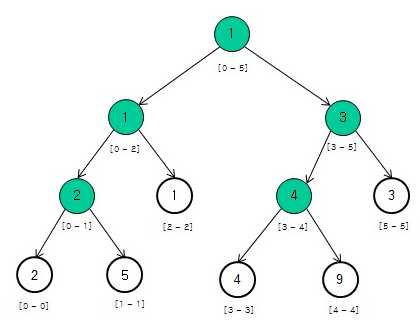
更一步，对于非叶子节点，若其表示的区间为[a,b]，那么左孩子表示的区间就为[a,(a+b)/2]，右孩子表示的区间就是[(a+b)/2+1,b]。

1. 树的构建

void create(int* segtree, int* data, int n_start, int n_end, int root = 1)
{
    //only leaf node stores the actual data
    if (n_end == n_start)
    {
        segtree[root] = data[n_start];
        return;
    }
    int mid = (n_end + n_start) / 2;
    create(segtree, data, n_start, mid, 2 * root);
    create(segtree, data, mid + 1, n_end, 2 * root + 1);
    segtree[root] = min(segtree[2 * root], segtree[2 * root + 1]);
 return;
}

2. 单点更新

void update_point(int* segtree, int root, int s, int e, int i, int num)
{
    if (s == e&&e == i)
    {
        segtree[root] = num;
        return;
    }
    int mid = (s + e) / 2;
    if (i <= mid)
        update_point(segtree, 2 * root, s, mid, i, num);
    else
        update_point(segtree, 2 * root + 1, mid + 1, e, i, num);
    segtree[root] = min(segtree[2 * root], segtree[2 * root + 1]);
}

3. 区间更新

区间更新就是对一个指定的区间中所有的数执行相同的操作，如都加2，都减2，等等。因为如果我们对每一个叶子节点都作更新（调用update_point），则一定会造成效率的低下。因此线段树采取的策略是“延迟更新”。所谓“延迟”，就是将“更新”的操作下一次更新或者查询的时候进行。这就使得更新操作不会马上进行，而给用户带来停顿感，如果以后的操作确实需要这些数据，再实际进行更新操作。还是以上面一个为例子。若现在需要对区间[0,2]中的所有数据加上2。因为延迟更新，我们只需要在线段树的代表[0,2]区间的节点的值加2即可，2+1=3，表明区间[0,2]之间的最小值为3，至此，更新操作完毕。因此当用户查找[a,b](2<=a<=b)之间的最小值时，还是按照普通的递归查询即可。但是更新/查找[a,b](a<=b<2)时，则必须对非叶子节点[0,2]的后代进行更新（因为此时之前只是对[0,2]这个非叶子节点更新了，它的后代节点依旧是“脏”数据）。因此必须需要额外的空间对节点进行标记，指示它是否被修改过。当修改或查询的时候，如果遇到被标记的节点，并在继续向下修改或查询的之前，需要将这种标记向下传递，向下传递意味着其左孩子和右孩子要执行与被标记节点同样的操作，即开始真正更新数据。

//called whenever perform update or query 
void propagate_down(int* segtree, int root)
{
    if (marker[root] == 0) return;
    //propagate the mark into the children of root
    marker[2 * root] += marker[root];
    marker[2 * root + 1] += marker[root];
    segtree[2 * root] += marker[root];
    segtree[2 * root + 1] += marker[root];
    //remove the mark of root
    marker[root] = 0;
}


void update_interval(int* segtree, int root, int s, int e, int n_start, int n_end, int add)
{
    //actually modify the node right here
    if (s == n_start&&e == n_end)
    {
        segtree[root] += add;
        marker[root] += add;
        return;
    }
    propagate_down(segtree, root);
    int mid = (s + e) / 2;
    if (n_end <= mid)
        update_interval(segtree, 2 * root, s, mid, n_start, n_end, add);
    else if (n_start>mid)
        update_interval(segtree, 2 * root + 1, mid + 1, e, n_start, n_end, add);
    else
    {
        update_interval(segtree, 2 * root, s, mid, n_start, mid, add);
        update_interval(segtree, 2 * root + 1, mid + 1, e, mid + 1, n_end, add);
    }
    segtree[root] = min(segtree[root * 2], segtree[2 * root + 1]);
}

4. 查询

int query(int* segtree, int root, int s, int e, int n_start, int n_end)
{
    if (n_start == s&&n_end == e)
        return segtree[root];
    int mid_seg = (s + e) / 2;
    propagate_down(segtree, root);
    if (n_end <= mid_seg)
        return query(segtree, 2 * root, s, mid_seg, n_start, n_end);
    else if (mid_seg + 1 <= n_start)
        return query(segtree, 2 * root + 1, mid_seg + 1, e, n_start, n_end);
    else
        return min(query(segtree, 2 * root, s, mid_seg, n_start, mid_seg),
            query(segtree, 2 * root + 1, mid_seg + 1, e, mid_seg + 1, n_end));
}