模拟退火算法研究

Posted 2020-10-18 木子丘

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了模拟退火算法研究相关的知识，希望对你有一定的参考价值。

模拟退火算法的物理背景：

模拟退火算法的核心思想与热力学的原理极为相似，在高温下，液体的大量分子彼此之间进行相对移动，如果液体慢慢冷却，原子的可动性就会消失，原子自行排列成行，形成一个纯净的晶体．如果温度冷却迅速，那它不一定能达到这个状态，这一个过程的本质在于，慢慢冷却，使原子在丧失可动性之前重新排列，达到低能状态的必要条件．

模拟退火算法的描述：

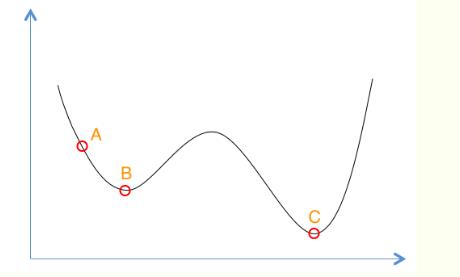
模拟退火算法实质是一种贪心算法，但和贪心算法不同的是，模拟退火算法在搜索过程中加入了随机的因素，它在搜索的过程中，会以一定的概率来接受比当前解要更差的解，因此有可能会跳出这个局部最优解，找到全局的最优值．

如图，假设从A点出发，搜索过程中找到了局部最优解B,模拟退火算法会以一定的概率接受比B更差的解，从而找到全局最优解C

模拟退火算法流程图

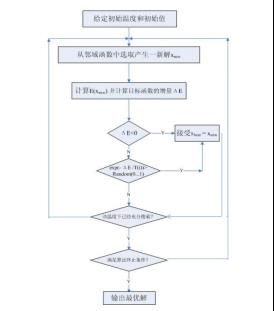
　模拟退火算法主要分三个步骤：　　

　　１．在当前解的基础上产生一个新解

　　２．利用Metropolis准则(即以e(- ∆E/T)的概率接受最优解)，判断新解是否被接受．　

　　３．当新解确定被接受时，用新解代替当前解，在此基础上进行下一轮实验，当新解被判定舍弃时，在原解的基础上进行下一轮实验

模拟退火算法伪代码：

模拟退火算法解决实际问题：

１．TSP问题：

旅行商问题(Traveling Salesman Problem,TSP),是数学领域一个著名问题之一，假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市，路径的选择目标是要求的路径的路程为所有路径中的最小值 .

执行代码

  1 #include <stdio.h>
  2 #include <stdlib.h>
  3 #include <math.h>
  4 #include <time.h>
  5 #include <algorithm>
  6 #include <iostream>
  7 using namespace std;
  8 
  9 int N;               //城市的数量
 10 const double T=3000; //初始温度
 11 const double k=0.98; //温度下降比例
 12 const double mint=1e-8; //温度的极值
 13 
 14 const int Oloop=1000;  //温度控制的最小值为t*0.98^20
 15 const int Iloop=15000; //寻找一定温度下的最大值
 16 const int lim=10000;  //概率选择次数的最大值
 17 
 18 double dist[100][100]; //任意两座城市之间的距离
 19 
 20 struct Path
 21 {
 22     int city[100];
 23     double len;  //路径的总长度
 24 };
 25 
 26 
 27 struct Point    //城市点的坐标
 28 {
 29     double x;
 30     double y;
 31 };
 32 
 33 Path bestpath;   //记录最优路径
 34 Path currpath;   //记录当前的路径
 35 Point p[100];     //各点的坐标
 36 
 37 void input()
 38 {
 39     scanf("%d",&N);
 40     for(int i=0;i<N;i++)
 41     {
 42         scanf("%lf%lf",&p[i].x,&p[i].y);
 43     }
 44 }
 45 
 46 //计算任意两点之间的距离
 47 void compu()
 48 {
 49     for(int i=0;i<N;i++)
 50     {
 51         for(int j=i+1;j<N;j++)
 52         {
 53             dist[i][j]=dist[j][i]=sqrt((p[i].x-p[j].x)*(p[i].x-p[j].x)+(p[i].y-p[j].y)*(p[i].y-p[j].y));
 54         }
 55     }
 56 }
 57 
 58 //初始化最优路径
 59 void init()
 60 {
 61     bestpath.len=0;
 62     bestpath.city[0]=0;
 63     for(int i=1;i<N;i++)
 64     {
 65         bestpath.city[i]=i;
 66         bestpath.len=bestpath.len+dist[i-1][i];
 67     }
 68     bestpath.len=bestpath.len+dist[0][N-1];
 69 }
 70 
 71 //随机选择目的优化路径，此处有两种方式，一是随机选取两个节点交换，二是随机排列
 72 Path choose(Path newpath)
 73 {
 74     int city1,city2;
 75     city1=(int)rand()%N;
 76     city2=(int)rand()%N;
 77     while(city1==city2)
 78     {
 79         city1=(int)rand()%N;
 80         city2=(int)rand()%N;
 81     }
 82     swap(newpath.city[city1],newpath.city[city2]);
 83     newpath.len=0;
 84     for(int i=1;i<N;i++)
 85     {
 86         newpath.len=newpath.len+dist[newpath.city[i-1]][newpath.city[i]];
 87     }
 88     newpath.len=newpath.len+dist[newpath.city[0]][newpath.city[N-1]];
 89     return newpath;
 90 }
 91 
 92 //模拟退火算法核心代码
 93 Path sa()
 94 {
 95     srand((unsigned)(time(NULL)));//时刻更新随机模板
 96     Path newpath=bestpath;
 97     Path currpath=bestpath;
 98     int pl=0; //以一定概率接受此路径的次数
 99     int pf=0;
100     double t2=T;
101     double t;
102     while(true){
103         for(int i=0;i<Iloop;i++)
104         {
105             newpath=choose(currpath);
106             t=newpath.len-currpath.len;
107             if(t<0)
108             {
109                 currpath=newpath;
110                 pl=0;
111                 pf=0;
112 
113             }
114             else
115             {
116                 double ran=rand()/(RAND_MAX+1.0);
117                 double exx=-t*1.0/t2*1.0;
118                 double ex=exp(exx);
119                 if(ran<ex)
120                 {
121                     currpath=newpath;
122                 }
123                 pl++;
124             }
125            if(pl>lim){
126                 pf++;
127                 break;
128            }
129         }
130         if(currpath.len<bestpath.len)
131         {
132             bestpath=currpath;
133         }
134         if(pf>Oloop||t2<mint)
135         {
136             break;
137         }
138         t2=t2*k;
139     }
140 }
141 
142 void Print()
143 {
144     for(int i=0;i<N;i++)
145     {
146         printf("%d ",bestpath.city[i]);
147     }
148     printf("length：%lf\\n",bestpath.len);
149 }
150 
151 int main()
152 {
153     for(int i=0;i<50;i++){
154         freopen("in.txt","r",stdin);
155         input();
156         compu();
157         init();
158         sa();
159         Print();
160     }
161     return 0;
162 }

验证数据：

执行过程

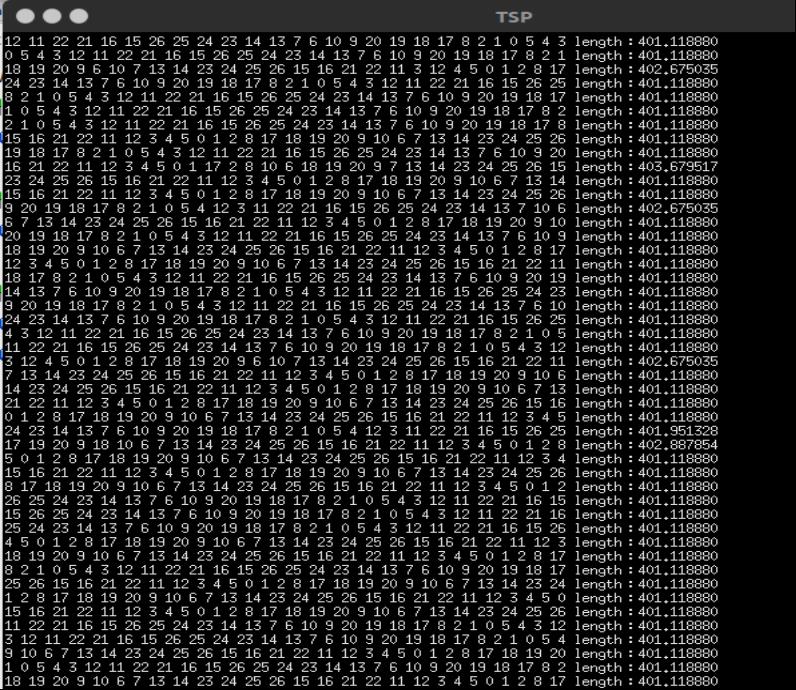
答案大概在401左右

２．求函数f(x,y)=5cos(xy)+xy+y^3的最小值，其中x的取值范围是(-5,5),y的取值范围是(-5,5)

执行代码：

进行过程中，容易出现陷入局部最优的问题

解决方法有：

  1 #include <stdio.h>
  2 #include <math.h>
  3 #include <time.h>
  4 #include <stdlib.h>
  5 #include <algorithm>
  6 #include <iostream>
  7 
  8 using namespace std;
  9 
 10 const double MAXx=5.0;          //x的最大值
 11 const double MINx=-5.0;         //x的最小值
 12 const double MAXy=5.0;          //y的最大值
 13 const double MINy=-5.0;         //y的最小值
 14 const double T=100;             //初始温度
 15 const double S=0.5;             //每次的变化量
 16 const double K=0.99;            //温度递减率
 17 const double ex=1e-9;
 18 double Bestx;
 19 double Besty;
 20 
 21 double functionf(double x1,double y1)       //所要求解的函数
 22 {
 23     return 5*cos(x1*y1)+x1*y1+y1*y1*y1;
 24 }
 25 
 26 void sa()
 27 {
 28     srand((unsigned)(time(NULL)));
 29     double currx,curry;
 30     double newx,newy;
 31     double Bestfun,currfun,newfun;
 32     double t=T;
 33     double de;
 34     Bestx=MINx+(MAXx-MINx)*rand()/RAND_MAX;
 35     Besty=MINy+(MAXx-MINy)*rand()/RAND_MAX;
 36     Bestfun=functionf(Bestx,Besty);
 37     currx=Bestx;
 38     curry=Besty;
 39     while(t>0.00001)
 40     {   int P=0;
 41         for(int i=0;i<10;i++)
 42         {
 43             int p=0;
 44             while(p==0)
 45             {
 46                 newx=currx+S*(MINx+(MAXx-MINx)*rand()/RAND_MAX);
 47                 if(newx>=MINx&&newx<=MAXx)
 48                 {
 49                     p=1;
 50                 }
 51             }
 52             de=functionf(currx,curry)-functionf(newx,newy);
 53             double dexp=exp(de/t);
 54             if(de>0)
 55             {
 56                 currx=newx;
 57                 //P++;
 58             }
 59             else
 60             {
 61                 if(dexp>(rand()/RAND_MAX+1))
 62                 {
 63                     currx=newx;
 64                     //P++;
 65                 }
 66             }
 67             for(int j=0;j<10;j++)
 68             {
 69                 p=0;
 70                 while(p==0){
 71                     newy=curry+S*(MINy+(MAXy-MINy)*rand()/RAND_MAX);
 72                     if(newy>=MINy&&newy<=MAXy)
 73                     {
 74                         p=1;
 75                     }
 76                 }
 77                 de=functionf(currx,curry)-functionf(newx,newy);
 78                 double dexp=exp(de/t);
 79                 if(de>0)
 80                 {
 81                     curry=newy;
 82                 }
 83                 else
 84                 {
 85                     if(dexp>rand()/RAND_MAX+1)
 86                     {
 87                         curry=newy;
 88                     }
 89                 }
 90             }
 91 
 92 
 93 
 94 //            double y2=curry;
 95 //            for(int j=0;j<10;j++)
 96 //            {
 97 //                p=0;
 98 //                while(p==0){
 99 //                    newy=y2+S*(MINy+(MAXy-MINy)*rand()/RAND_MAX);
100 //                    if(newy>=MINy&&newy<=MAXy)
101 //                    {
102 //                        p=1;
103 //                    }
104 //                }
105 //                de=functionf(currx,y2)-functionf(newx,newy);
106 //                double dexp=exp(de/t);
107 //                if(de>0)
108 //                {
109 //                    y2=newy;
110 //                }
111 //                else
112 //                {
113 //                    if(dexp>rand()/RAND_MAX+1)
114 //                    {
115 //                        y2=newy;
116 //                    }
117 //                }
118 //            }
119 //
120 //            if(functionf(currx,y2)<functionf(currx,curry))
121 //            {
122 //                curry=y2;
123 //            }
124 //            if(P>300){
125 //               P=0;
126 //                break;
127 //            }
128 
129 
130         }
131         if(functionf(currx,curry)<functionf(Bestx,Besty))
132         {
133                 Bestx=currx;
134                 Besty=curry;
135         }
136         t=t*K;
137     }
138 }
139 
140 int main()
141 {
142     for(int i=1;i<205;i++)
143     {
144         sa();
145         printf("%f ",functionf(Bestx,Besty));
146         if(i%6==0)
147         printf("\\n");
148     }
149     printf("\\n");
150 }

执行过程

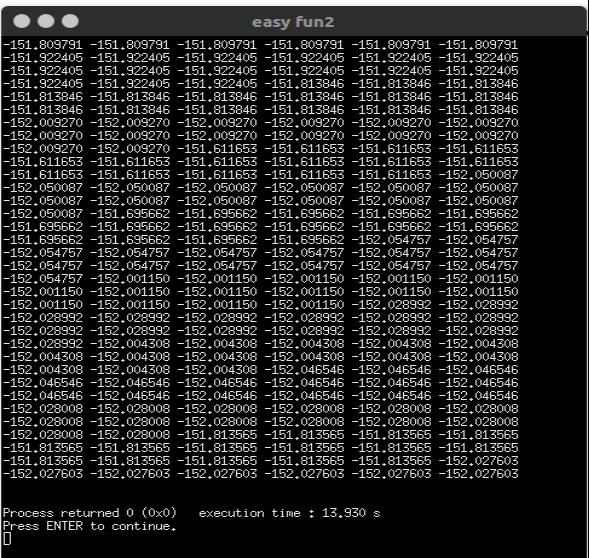
答案在-151.1左右

总结：

模拟退火算法计算过程简单，引入概率跳出局部最优解，全局性较强．但在执行过程中，算法的执行时间较长，相关参数的变化对算法性能影响大，例如，如果在某一温度下充分搜索，很容易陷入到局部最优解中，并且收敛速度慢，但如果不充分搜索，那么很难的到全局最优解．所以，约束条件的选择，参数控制都非常关键，还有待进一步研究．

以上是关于模拟退火算法研究的主要内容，如果未能解决你的问题，请参考以下文章

Matlab：数模06-模拟退火模型

模拟退火算法(转自-ranjiewen的博客园！)

模拟退火算法通俗讲解

两种改进的模拟退火算法求解大值域约束满足问题1.0

OpenAI Gym 关于CartPole的模拟退火解法