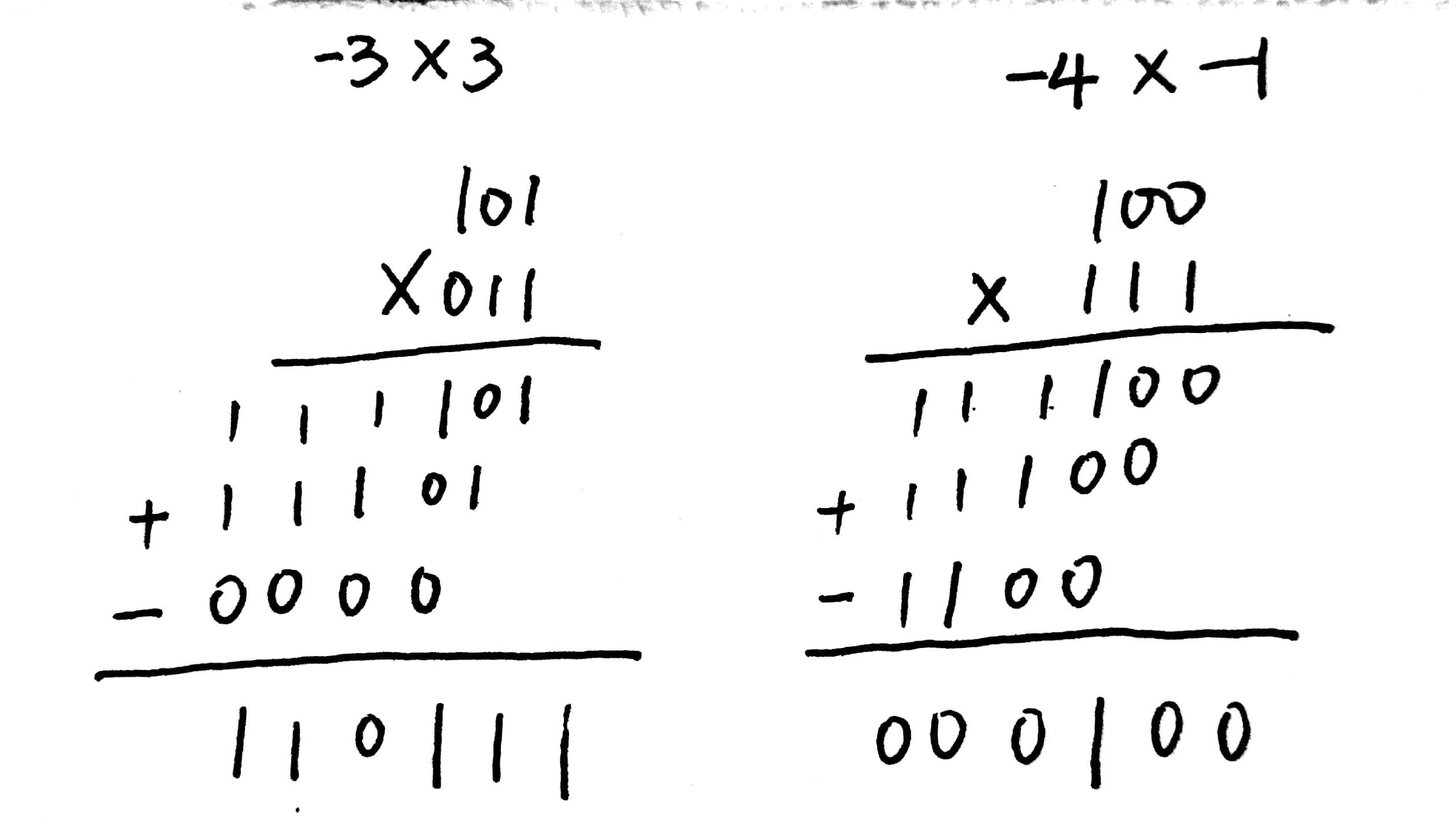一、信息存储
1.机器级程序将存储器视为一个非常大的字节数组,称为虚拟存储器,每个字节都有一个唯一的数字来标识,称为地址,所有可能地址的集合称为虚拟地址空间。
2.每台计算机都有一个字长,指明指针数据的标称大小。32位程序和64位程序区别在于该程序如何编译,而不是其运行的机器类型。C语言各种数据类型分配的字节数如下:
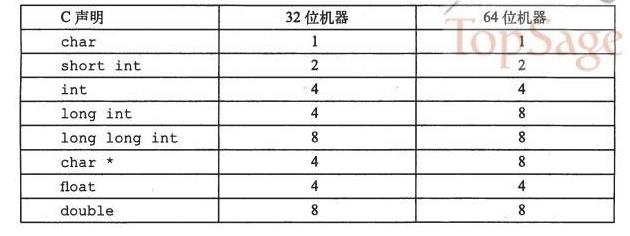
int32_t和int64_t分别为4个字节和8个字节,数据大小固定,不随编译器和机器设置而变化。
3.寻址与字节顺序
- 最高有效字节在最前面即低地址的为大端法,主要用于IBM与Sun机器
- 最低有效字节在最前面的为小端法,主要用于Intel及其兼容机
在Linux和Windows运行不同程序对象的字节表示程序结果如下,可以看出它们都是小端法机器:

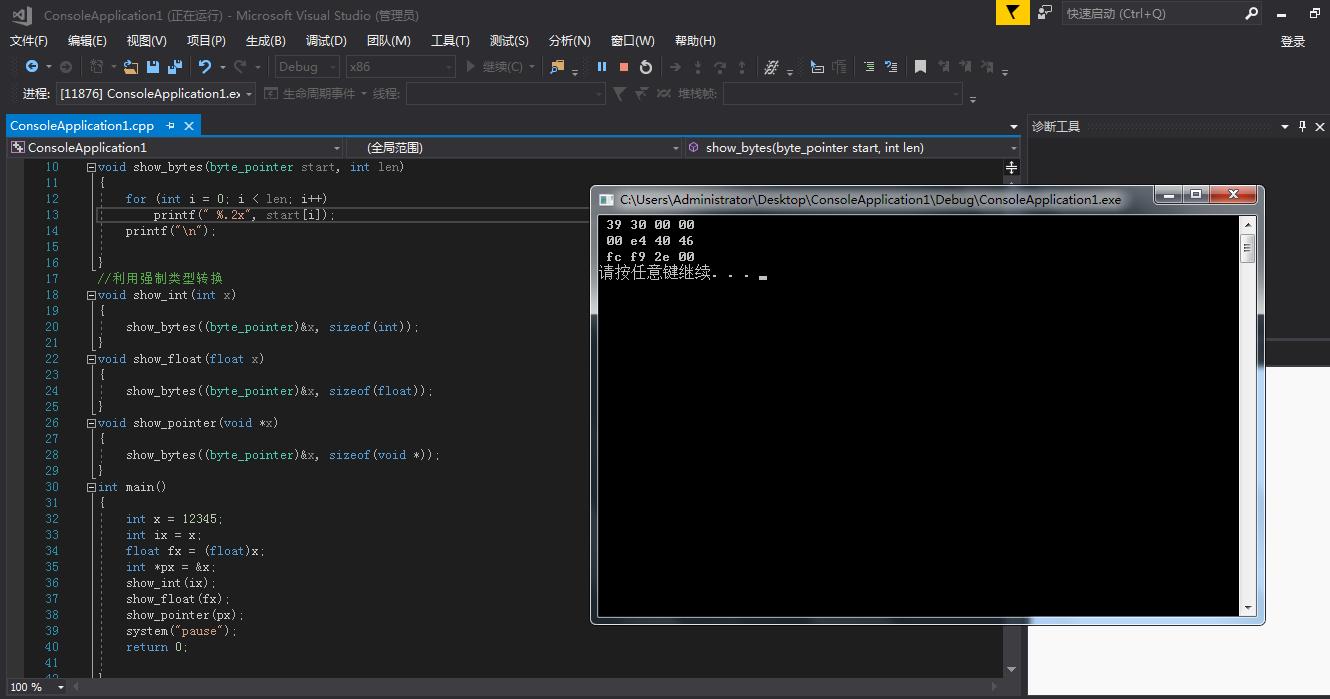
4.布尔运算&对|,|对&有分配律。位向量的应用对集合编码。有很多不同的信号会中断程序执行,通过指定一个位向量掩码,有选择地使能或屏蔽一些信号,1表示信号i是有效的,0表示该信号被屏蔽。
5.逻辑运算认为非0就是true,而0表示false;逻辑运算如果第一个表达式能确定结果就不会对第二个求值。
6.移位运算
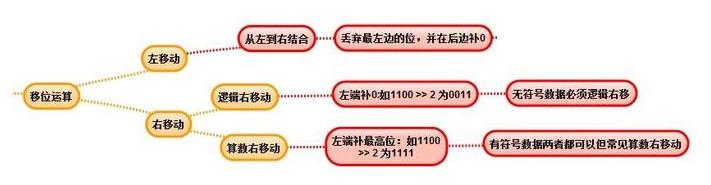
二、整数表示
1.补码的最高有效位为符号位,无符号数、补码编码具有唯一性。最小的负数TMin为[1000]结果为-8,最大的正数TMax[0111]结果为7,得出|TMin| = |TMax| + 1,补码范围的不对称性来源于一半的位模式表示负数,一半的位模式表示非负数(0是非负数,故多出一个数)。-1和UMax有同样的位表示,0在两种表示中都是全0。

2.有符号数和无符号数之间的转换
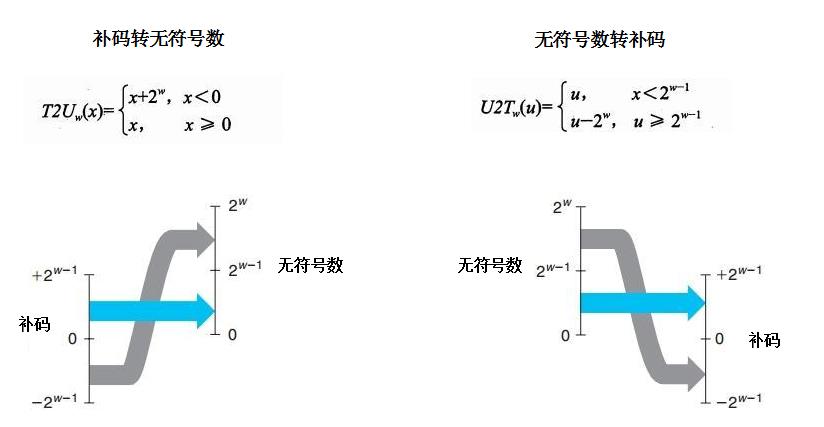
C语言中,如果执行一个运算,它的一个运算符是有符号另外一个无符号,那么就会隐式的把有符号的参数强制类型转换为无符号数,并假设这两个都是非负数来进行计算。如比较:-1 < 0U的值时,先将-1转无符号数:4294967295 < 0U 就会出现问题。
3.扩展位表示:将一个数据大小改变,和无符号有符号之间这两组转换的相对顺序,会影响一个程序的行为。如果将short转为unsigned时,就会先改变大小,然后再完成有符号到无符号的转变。如short x = -12345 ,则(unsigned)x=(unsigned)(int)x,先将0X CF C7扩展成0X FF FF CF C7,然后再进行到无符号数的转化,最后得到4294954951。
4.截断数字:
- 对于无符号数:15(1111) 截断3位,就是将15 mod 8(2的3次方) = 7 (111)
- 对于有符号数:-1(1111) 截断3位,就是先将-1转为无符号数15,然后mod 8 = 7(111),然后再把7转为有符号数-1
三、整数运算
1.无符号数和补码的加法

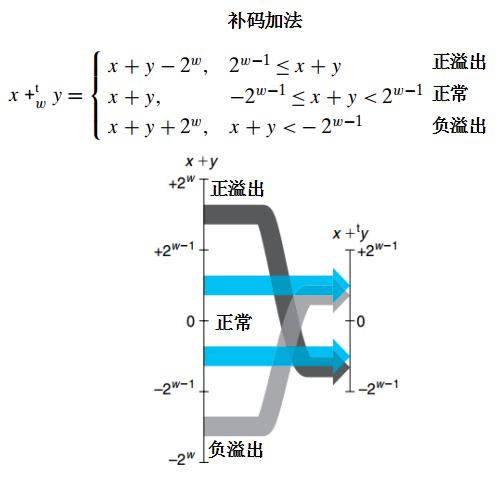
如正溢出[0101] +[0101] = 5 + 5 = 10 = [01010]截断最高位0结果为[1010]=-6; 负溢出 [1000]+ [1000]= -8 + -8 = -16 = [10000]截断高位1结果为[0000]=0
2.无符号数和补码的乘法:如果w位的两个数相乘,结果最大可能是2w位,C语言中使用固定精度的运算,这就导致了结果只能截断到w位,只保留真实值的低w位。
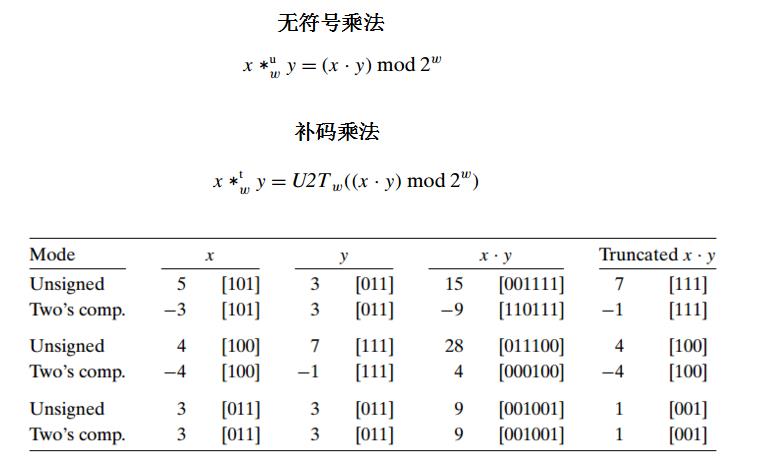
3.乘法运算太慢,于是编译器就使用移位和加法指令来替代乘以常数。除法指令更慢,经常用右移来代替。乘以常数(左移),除以2的幂(右移)。整数除法舍入到0。除以2的幂的补码除法向下舍入,如-7/2不是-3而是-4,通过移位前“偏置”这个值,来向上舍入。X/Y(向上舍入) = (X+Y-1)/Y(向下舍入),例如-30/4(向上舍入)=-7=-27/4(向下舍入)。
四、浮点数
1.IEEE浮点表示
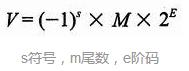
- 规格化的值: E≠0或者E≠255(exp的位模式不全为0或1),阶码段被解释成有偏置值形式的有符号整数
E=e-Bias,e为无符号数,Bias = 2的k-1次方-1。M尾数定义为1+f(隐含了以1开头的表示) - 非规格化值:非规格化数提供了一种表示数值0的方法,也表示非常接近于0和0的数。exp的位模式全为0,
E=1-Bias,M = f - 特殊值:exp的位模式全为1。当M=0时得到无穷大s=0是正无穷大,s=1时是负无穷大;当M≠0时结果值为Not a Number(NAN)
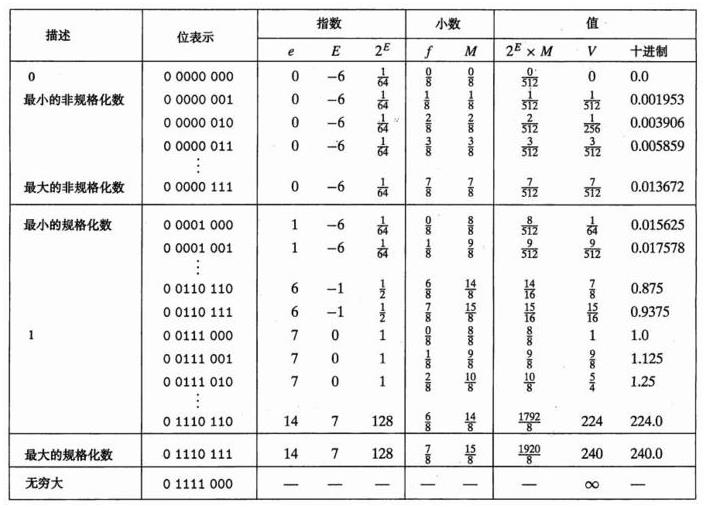
非规格化偏置被设置成1-Bias,而不是-Bias,其实是补偿非规格化的尾数没有隐含的1开头这一事实。
将整数12345二进制表示[11000000111001]转化为单精度浮点表示,将二进制左移13位表示为1.1000000111001 X 2的13次方。为了用IEEE单精度形式来编码,丢弃开头的1,并在末尾增加10个0,M = [10000001110010000000000]。为了构造阶码字段,用13加上偏置量127得140,二进制表示为[10001100],再加上符号位0最后结果就是[01000110010000001110010000000000]。
12345(0X3039)和12345.0(0X4640E400)的位级表示如下,可以看到浮点数尾数M和0x3039恰好相差最高位1。这个位就是隐含的开头的位1。

2.由于舍入而产生的丢失精度,浮点数的运算中不具有结合性,具有交换性、单调性。
3.如果机器使用IEEE浮点,那么就是向偶数舍入。
五、问题及解决
p68页!为什么-3乘以3得到[110111],用补码乘法如何列式计算?
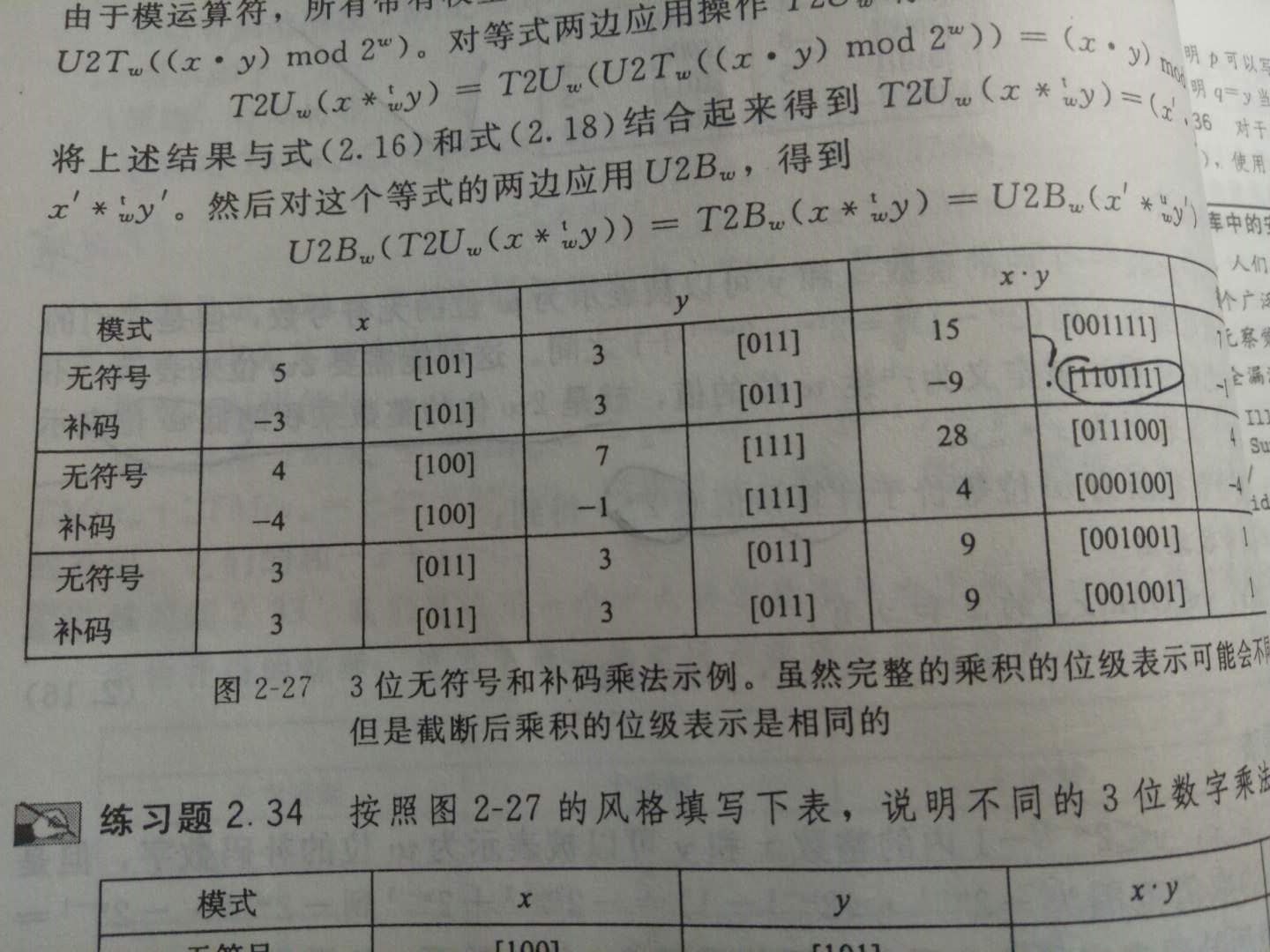
经过查资料知道了和普通乘法不同,补码乘法需要拓展前面的位(符号拓展)不能默认为0,最高有效位Y2是符号位,权重是-2^(w-1),所以要减去:

因此101乘以011,199乘以111列式如下: