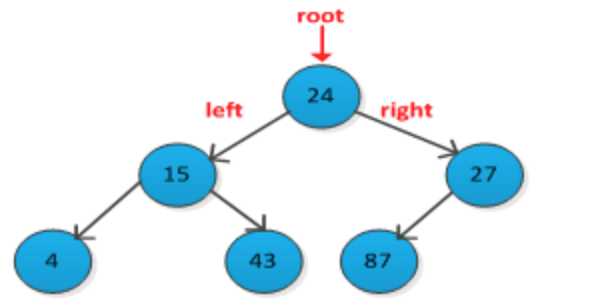
1. 二叉树
(Binary Tree)是一种特殊的树型结构,每个节点至多有两棵子树,且二叉树的子树有左右之分,次序不能颠倒。
2. 特点
(1)在二叉树中的第i层上至多有2^(i-1)个结点。
(2)深度为k的二叉树至多有2^k-1个节点(k>=1)。
(3)对任何一棵二叉树T,如果其终端结点数目为n0,度为2的节点数目为n2,则n0=n2+1。(和(2)很像)
满二叉树:深度为k且具有2^k-1个结点的二叉树。即满二叉树中的每一层上的结点数都是最大的结点数。
完全二叉树:深度为k具有n个结点的二叉树,当且仅当每一个结点与深度为k的满二叉树中的编号从1至n的结点一一对应。
3. 存储结构
可以采用顺序存储数组和链式存储二叉链表两种方法来存储二叉树。经常使用的二叉链表方法,因为其非常灵活,方便二叉树的操作。
4. 遍历二叉树
命名按照根节点访问的顺序
(1)先根遍历(先序遍历):根节点,左节点,右节点。[24, 15, 4, 43, 27, 87]
(2)中根遍历(中序遍历):左节点,根节点,右节点。[4, 15, 43, 24, 87, 17]
(3)后根遍历(后序遍历):先遍历最右边,然后左边。[4, 43, 15, 87, 27, 24]