二叉树及特殊二叉树(满二叉树完全二叉树二叉排序树平衡二叉树)的定义和性质(附详细推理过程)
Posted 薛定谔的猫ovo
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉树及特殊二叉树(满二叉树完全二叉树二叉排序树平衡二叉树)的定义和性质(附详细推理过程)相关的知识,希望对你有一定的参考价值。
二叉树的定义
二叉树是树的特殊形式,其特点是每个结点至多只有两棵子树,也就是说二叉树中不存在度大于2的结点,并且二叉树的子树有左右之分,其次序不能任意颠倒,即二叉树是有序树。
与树相似,二叉树也以递归的形式定义。二叉树是n(n≥0)个结点的有限集合。
1)或者为空二叉树,即n = 0,
2)或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是以可二叉树。
二叉树是有序树,故二叉树的基本形态有以下五种:
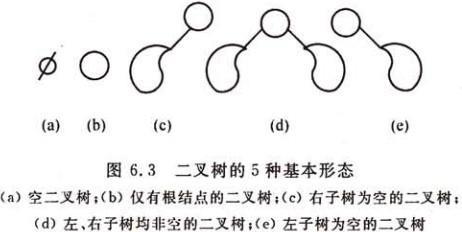
注意二叉树与度为2的有序树的区别:
1)度为2的树至少有3个结点,不能是空树;而二叉树可以为空。
2)度为2的有序树的孩子结点的左右次序是相对于另一个孩子结点而言的,若某个结点只有一个孩子结点,则这个孩子结点就无须区分其左右次序;而二叉树的结点次序不是相对于另一结点而言的,而是确定的,即二叉树无论其孩子数是否为2,均需要确定其左右次序。
二叉树的性质
1)非空二叉树上的叶子结点数等于度为2的结点数加1,即n0 = n2 + 1。
证明:设度为0、1、2的结点个数分别为n0、n1、n2,那么结点总数n = n0+n1+n2。
再看二叉树中的分支数,除了根结点外,其余每个结点都有一个分支进入,设B为分支总数,则n = B + 1。
由于这些分支是由度为1或者度为2的结点射出的,所以又有B = n1+2n2。
故综上n0 = n2 + 1。
2)非空二叉树上第k层至多有2k-1个结点(k ≥ 1)。
求至多有多少个结点,那么到第k层为止应该是一个满二叉树,那么第 k 层的结点数 = 2*(第 k-1 层的结点数) =2*2*(第k-2层的结点数) = … = 2k-1*(第1层的结点数)= 2k-1
3)高度为h的二叉树至多有2h-1个结点(h ≥ 1)。
求至多有多少个结点,则该树应是满二叉树,其结点数为:
20+21+22+…+2h-1 = 2h-1。
几个特殊的二叉树
满二叉树
一棵高度为h,且含有2h-1个结点的二叉树称为满二叉树,即树中的每层都含有最多的结点,如下图所示:
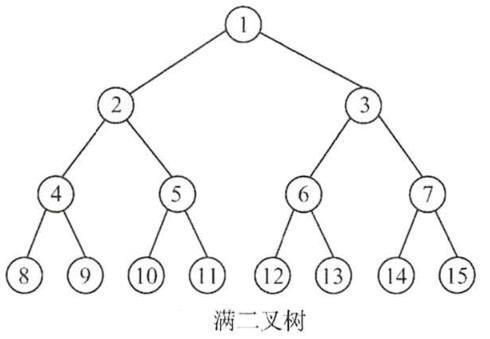
满二叉树的特点及性质:
1)满二叉树的叶子都集中在二叉树的最下一层,并且除叶子结点之外的每个结点度数均为2。
2)对于满二叉树按层编号,根结点编号为1,自上而下,自左至右,如上图所示。那么对于编号为 i 的结点:
若有双亲,则其双亲为⌊i /2⌋;
若有左孩子,则左孩子为2i;若有右孩子,则右孩子为2i+1.
完全二叉树
设一个高度为h、有n个结点的二叉树,当且仅当其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应时,称为完全二叉树。即完全二叉树中除了最后一层外,其余每层都含有最多结点数,如下图所示:
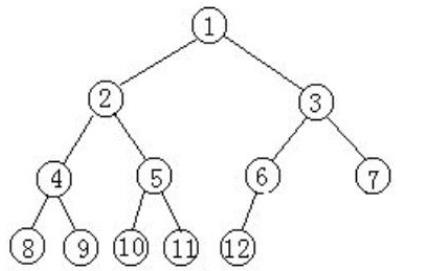
完全二叉树的特点及性质:
1)若编号i ≤ ⌊n /2⌋,则结点 i 为分支结点,否则为叶子结点。
对于最后一个结点,其编号为n,那么其双亲结点的编号为⌊n /2⌋,自这个结点之后,再无分支结点,剩余均为叶子结点,可结合上图以及特点4进行理解。
2)叶子结点只可能在层次最大的两层上出现。对于最大层次中的叶子结点,都依次排列在该层的最左边的位置上。
3)若有度为1的结点,则只可能有一个,且该结点只有左孩子而无右孩子。
4)按层序编号后,一旦出现某结点(编号为i)为叶子结点或只有左孩子,则编号大于i的结点均为叶子结点。
5)若n为奇数,则每个分支结点都由左孩子和右孩子;若n为偶数,则编号最大的分支结点(编号为n/2)只有左孩子,没有右孩子,其余分支结点左、右孩子都有。
6)具有n个结点的完全二叉树的高度为⌊log2n⌋ + 1 或 ⌈log2(n+1)⌉ 。
由二叉树的性质可知,高度为h的二叉树至多有2h-1个结点(h ≥ 1)。
设完全二叉树的高度为h,则有n ≤ 2h-1,解得h ≥ log2(n+1),由于h为整数,故⌈log2(n+1)⌉。
完全二叉树的倒数第二层的结点数为2h-1-1,最后一层的结点数至多为2h-1,那么完全二叉树结点数n的取值范围为2h-1-1 ≤ n <2h-1,解得h-1 ≤ log2n <h,由于h为整数,故取整h = ⌊log2n⌋ + 1 。
7)结点 i 所在的层次(深度)为⌊log2 i⌋ + 1。
证明与性质6同理。
二叉排序树
一棵二叉树或者是空二叉树,或者是具有如下性质的二叉树:
1. 左子树上的所有结点的关键字均小于根结点的关键字;
2. 右子树上的所有结点的关键字均大于根结点的关键字;
3. 左子树和右子树又各是一棵二叉排序树。
一棵二叉排序树的实例如下图所示:
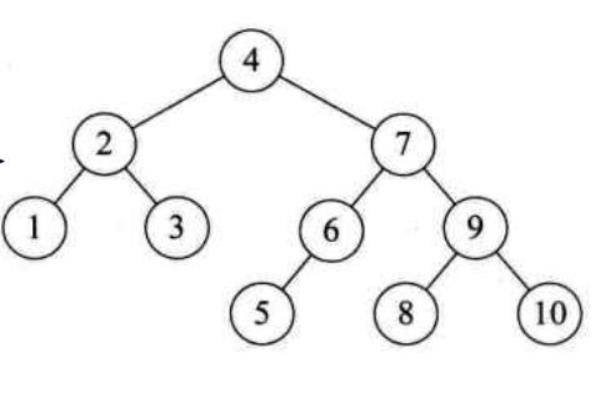
平衡二叉树
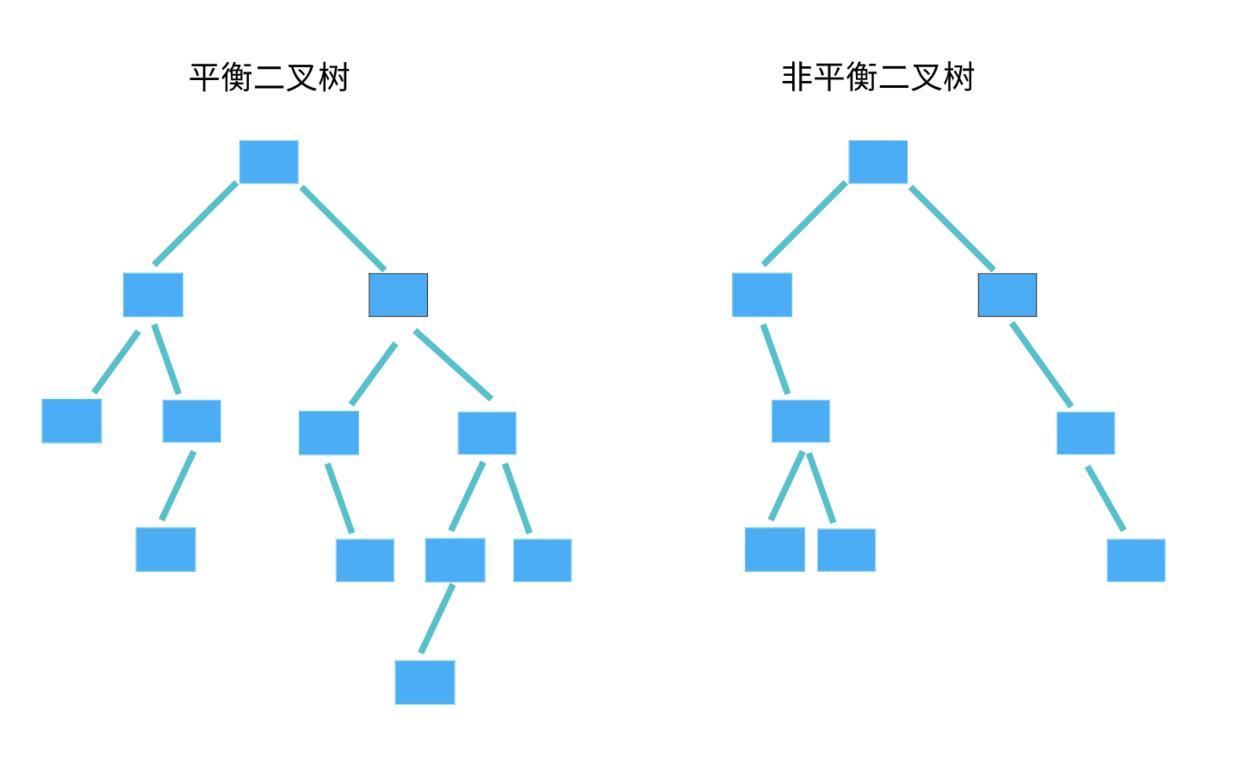
树上任一结点的左子树和右子树的深度之差不超过1。
一棵平衡二叉树的形状如下图所示:
以上是关于二叉树及特殊二叉树(满二叉树完全二叉树二叉排序树平衡二叉树)的定义和性质(附详细推理过程)的主要内容,如果未能解决你的问题,请参考以下文章