Apriori算法实现

Posted 2020-10-17 温酒待君归

本次缑老师布置的作业较为简单，其原理实现也是非常的清楚。

关于关联规则，细想一下，其本质，笔者窃以为：仍然是分类的思想，其本质为，可以划分为一类的item，其内部就有一定的相关性，那么，挖掘的本质，就是在分类以后，找到同一类不同item中的相关性（为啥可以分到同一类中去）。

笔者刚才荡了一段代码，发现其可移植性非常好。现在，下面就贴出代码、结果和原网址。有兴趣的同学可以继续参考一下。

实现环境：Ubuntu下Python2.7（Ubuntu自带）

其代码如下：

# -*- coding: utf-8 -*-
"""
Apriori exercise.
Created on Fri Nov 27 11:09:03 2015

@author: 90Zeng
"""

def loadDataSet():
    \'\'\'创建一个用于测试的简单的数据集\'\'\'
    return [ [ 1, 3, 4 ], [ 2, 3, 5 ], [ 1, 2, 3, 5 ], [ 2, 5 ] ]

def createC1( dataSet ):
    \'\'\'
    构建初始候选项集的列表，即所有候选项集只包含一个元素，
    C1是大小为1的所有候选项集的集合
    \'\'\'
    C1 = []
    for transaction in dataSet:
        for item in transaction:
            if [ item ] not in C1:
                C1.append( [ item ] )
    C1.sort()
    return map( frozenset, C1 )

def scanD( D, Ck, minSupport ):
    \'\'\'
    计算Ck中的项集在数据集合D(记录或者transactions)中的支持度,
    返回满足最小支持度的项集的集合，和所有项集支持度信息的字典。
    \'\'\'
    ssCnt = {}
    for tid in D:
        # 对于每一条transaction
        for can in Ck:
            # 对于每一个候选项集can，检查是否是transaction的一部分
            # 即该候选can是否得到transaction的支持
            if can.issubset( tid ):
                ssCnt[ can ] = ssCnt.get( can, 0) + 1
    numItems = float( len( D ) )
    retList = []
    supportData = {}
    for key in ssCnt:
        # 每个项集的支持度
        support = ssCnt[ key ] / numItems
        
        # 将满足最小支持度的项集，加入retList
        if support >= minSupport:
            retList.insert( 0, key )
            
        # 汇总支持度数据
        supportData[ key ] = support
    return retList, supportData
#######################################

if __name__ == \'__main__\':
    # 导入数据集
    myDat = loadDataSet()
    # 构建第一个候选项集列表C1
    C1 = createC1( myDat )
    
    # 构建集合表示的数据集 D
    D = map( set, myDat )
    # 选择出支持度不小于0.5 的项集作为频繁项集
    L, suppData = scanD( D, C1, 0.5 )
   
    print u"频繁项集L：", L
    print u"所有候选项集的支持度信息：", suppData
################################################
# Aprior算法
def aprioriGen( Lk, k ):
    \'\'\'
    由初始候选项集的集合Lk生成新的生成候选项集，
    k表示生成的新项集中所含有的元素个数
    \'\'\'
    retList = []
    lenLk = len( Lk )
    for i in range( lenLk ):
        for j in range( i + 1, lenLk ):
            L1 = list( Lk[ i ] )[ : k - 2 ];
            L2 = list( Lk[ j ] )[ : k - 2 ];
            L1.sort();L2.sort()
            if L1 == L2:
                retList.append( Lk[ i ] | Lk[ j ] ) 
    return retList

def apriori( dataSet, minSupport = 0.5 ):
    # 构建初始候选项集C1
    C1 = createC1( dataSet )
    
    # 将dataSet集合化，以满足scanD的格式要求
    D = map( set, dataSet )
    
    # 构建初始的频繁项集，即所有项集只有一个元素
    L1, suppData = scanD( D, C1, minSupport )
    L = [ L1 ]
    # 最初的L1中的每个项集含有一个元素，新生成的
    # 项集应该含有2个元素，所以 k=2
    k = 2
    
    while ( len( L[ k - 2 ] ) > 0 ):
        Ck = aprioriGen( L[ k - 2 ], k )
        Lk, supK = scanD( D, Ck, minSupport )
        
        # 将新的项集的支持度数据加入原来的总支持度字典中
        suppData.update( supK )
        
        # 将符合最小支持度要求的项集加入L
        L.append( Lk )
        
        # 新生成的项集中的元素个数应不断增加
        k += 1
    # 返回所有满足条件的频繁项集的列表，和所有候选项集的支持度信息
    return L, suppData
###################################################
if __name__ == \'__main__\':
    # 导入数据集
    myDat = loadDataSet()    
    # 选择频繁项集
    L, suppData = apriori( myDat, 0.5 )
    print u"频繁项集L：", L
    print u"所有候选项集的支持度信息：", suppData

其结果为：

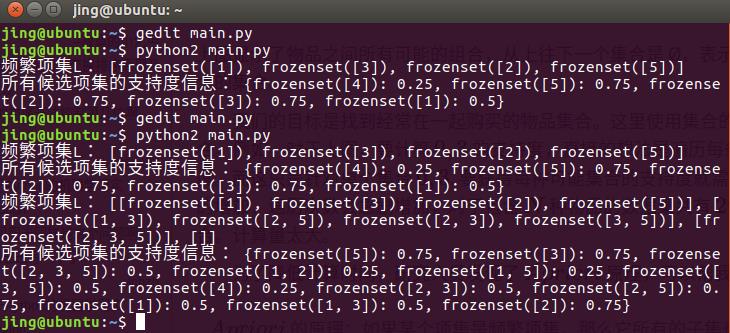
其含义可以从结果直观的看出。这也是Python的优势，其开源性保证了代码库的量足够大。

原网址：https://www.cnblogs.com/90zeng/p/apriori.html

欢迎大家探讨。