数据结构和算法之排序一:归并排序
Posted GoNewLife
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构和算法之排序一:归并排序相关的知识,希望对你有一定的参考价值。
我们不得不承认一个事实,java学习过程中如果我们掌握了各种编程手段和工具,确实可以做一些开发,这就是一些培训机构敢告诉你几个月就能掌握一门语言的原因。但是随着时间的发展,我们总会感觉,这一类人如果不提升自己,最后也只会是一个码农。技术会日新月异,随时在发展更新换代,但是这几十年,有谁说过算法会过时,如果我们说java语言的发动机是各种开发手段和技术,那么我们可以毫不客气的说算法会是他的灵魂。一个程序员的提升和拔高一定是万丈高楼平地起,那么我希望这个地基一定是数据结构和算法,掌握这些原理以后其实在以后的学习过程当中我们会异常的轻松。
首先,我们需要掌握几种最基本的排序方式,比如简单排序,插入排序,快速排序,堆排序,冒泡排序,选择排序,希尔排序,归并排序。每一种排序方式都有自己的特点,数据量的大小或者说对时间复杂度,空间复杂度的要求都可以选择合适的排序方式进行排序。就我个人而言,因为在我学习的过程中对归并排序情有独钟,所以今天我们在这里介绍一下归并排序。我们这将演示归并排序的java实现代码,以及归并的特点,它的时间复杂度和空间等等的问题计算。
一:归并排序的特点:
归并排序的特点第一点就是它是一个比较有代表性的分而治之思想的排序方式,其中渗透着递归的思想,当我们面对一大堆复杂的复杂的数据无从下手时,或许分而治之就是我们的首选,这就确定了归 并排序最好是在数据量比较大,对空间复杂度要求不高,对时间复杂具有一定要求的情况下使用。因为它在不断的递归拆分数据的过程中会占用栈的空间。说到这里可能有点迷糊,那我们直接上代码 看如何实现归并排序。
二:代码实现:
第一步:我们称之为归并,那么必然涉及到了合并,如果有合并,那么必然会有相对应的拆分。在这一步我们对应的就是sort方法,让一个完整的数组进行不断的拆分,直到最后的数据单元是一个单独 的数据位置,这时候在进行第二步,就是从小往上不断地对分开的数据进行整合。
第二步:也就是我们看到的mergeArray()方法,它是通过一个临时数组最为一个临时的容器,将比较过后的有序数组存储进去,然后再取出赋值给原始数据。这里需要提出几个比较需要理解的地方,
第一点:就是我们在进行合并的时候是合并middle数据两边的数据集合,通过比较,让小的进入临时数组,角标加一,在进行比较,直到一个数据集合到底位置。
第二点:我们在进行比较以后必然会有一个数据集合会留下一些数据没有进行插入,这时候我们就比较他们的开始和结束的角标,如果不等于那么就把这个数据集合里面的数据继续通过while 循环加入我们的临时数组中。
第三点:我们在最后的时候,把临时数组中的数据加入原始数组,必须记住要加上start这个数值,因为我们都知道在合并的时候,我们左右是同时进行的,左边的数据可能是从0开始,但是右 边的数据就不见得了,所以我们要加上合并开始的位置start。
第四点:一定要注意一个事情,算法看懂很困难,但是我们或许需要实践,在运算的逻辑处理不理解时,可以在草稿纸上进行过程分解,或者通过源代码进行debag模式,分析数据的走向。
1 public static void sort(int arr[],int emp[],int start,int end){ 2 //对是否继续拆分递归进行判断 3 int middle = start + (end - start) / 2; 4 if(start < end){ 5 sort(arr,emp,start,middle);//让左边的数据进行拆分并实现有序 6 sort(arr,emp,middle + 1,ens);//让右边的数据进行拆分并实现有序 7 mergeArray(arr,emp,start,middle,end);//进行合并 8 } 9 } 10 public static void mergeArray(int arr[],int emp[],int start,int middle,int end){ 11 int i = start,j = middle; 12 int k = middle + 1,z = end; 13 int x = 0; 14 //判断那个数据大小插入临时数组 15 while(i <= j&& k <= z){ 16 if(arr[i] < arr[k]){ 17 emp[x++] = arr[i++]; 18 } else{ 19 emp[x++] = arr[k++]; 20 } 21 } 22 //当我们经拆分好的两边数据插入临时数组以后肯定还有未完成的数据在原始数组中 23 //继续进行数据清理,加入临时数组 24 while(i <= j){ 25 emp[x++] = arr[i++]; 26 } 27 while(k <= z){ 28 emp[x++] = arr[k++]; 29 } 30 //所有数据进入临时数组以后我们将数据导出,放入原始数组中,这些数据必然有序 31 for(i = 0;i < x;i++){ 32 arr[start + i] = emp[i]; 33 } 34 35 }
三:算法过程分析图:
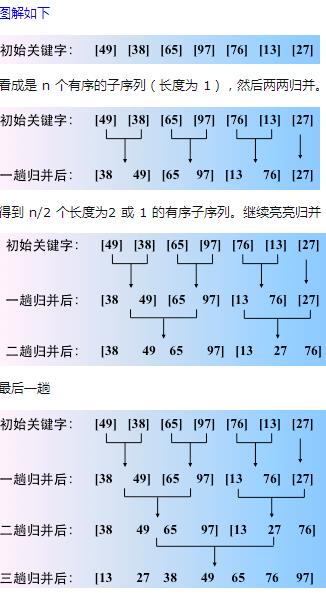
四:归并的时间复杂度计算和分析: 对于这一块来说我们或许可以试着去尝试理解,对于各方面的综合考虑来说对于初学者可能比较有难度。
可以说合并排序是比较复杂的排序,特别是对于不了解分治法基本思想的同学来说可能难以理解。总时间=分解时间+解决问题时间+合并时间。
分解时间:把一个待排序序列分解成两序列,时间为一常数,时间复杂度o(1).
解决问题时间:两个递归式,把一个规模为n的问题分成两个规模分别为n/2的子问题,时间为2T(n/2).合并时间复杂度为o(n)。
总时间:T(n)=2T(n/2)+o(n).这个递归式可以用递归树来解,其解是o(nlogn).此外在最坏、最佳、平均情况下归并排序时间复杂度均为o(nlogn).从合并过程中可以看出合并排序稳定。
用递归树的方法解递归式T(n)=2T(n/2)+o(n):假设解决最后的子问题用时为常数c,则对于n个待排序记录来说整个问题的规模为cn。

从这个递归树可以看出,第一层时间代价为cn,第二层时间代价为cn/2+cn/2=cn.....每一层代价都是cn,总共有logn+1层。所以总的时间代价为cn*(logn+1).时间复杂度是o(nlogn)
以上是关于数据结构和算法之排序一:归并排序的主要内容,如果未能解决你的问题,请参考以下文章