数据结构和算法 – 2.基础查找算法

Posted 2020-07-03 【唐】三三

有两种对列表内数据进行查找的方法：顺序查找和二叉查找。当数据项在列表内随机排列的时候可以使用顺序查找，而当数据项在列表内有序排列的时候则会用到二叉查找。

顺序查找

二叉查找

1.顺序查找

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace 数据结构和算法
{
    class _2
    {
        public readonly static int[] arrayList = new int[] { 312, 564, 1254, 145, 212, 884, 145, 1212, 443, 56, 222 };

        static void Main()
        {
            int[] numbers = new int[100];
            for (int i = 0; i < arrayList.Length; i++)
            {
                numbers[i] = arrayList[i];
            }

            int searchNumber;
            Console.WriteLine("输入一个数字：");
            searchNumber = int.Parse(Console.ReadLine());

            bool found;
            found = seqSerch(numbers, searchNumber);
            if (found)
            {
                Console.WriteLine(searchNumber +"找到了!");
            }
            else
            {
                Console.WriteLine(searchNumber + "没有在数组中!");
            }
            Console.ReadKey();
        }
        static bool seqSerch(int[] arr, int sValue)
        {
            for (int i = 0; i < arr.Length; i++)
            {
                if (arr[i] == sValue)
                {
                    return true;
                }
            }
            return false;
        }
    }
}

 

 

自组织数据加快顺序查找速度

当要查找的数据元素就在数据集合的开始处时就会产生最快速的成功查找。通过找到数据项后把它移动到数据集合开始处的方法可以确保成功定位数据项。
这种策略的含义就是通过把频繁查找的数据项放在数据集合开始处的方法来最小化查找的次数。最终的结果就是所有最频繁查找的数据项都会被放置在数据集合的开始部分。这是自组织的一个实例，这是因为数据集合不是在程序运行之前由程序员组织的，而是在程序运行期间由程序自身组织的。
既然要查找的数据大概会遵循“ 80–20”规则，这使得允许数据进行组织变得有意义了。其中，“ 80-20”原则意味着在数据集合上 80%的查找操作都是为了查找到数据集合内 20%的数据。自组织将最终把 20%的数据放在数据集合的开始部分，这样顺序查找就可以快速地找到它们了。
像这样的概率分布被称为是帕累托分布，它是以 19 世纪后期通过研究收入和财富的扩散而发现这类概率分布的科学家 Vilfredo Pareto 的名字命名的。

static int SeqSearch(int sValue)
        {
            for (int index = 0; index < arr.Length - 1; index++)
                if (arr[index] == sValue)
                {
                    swap(index, index - 1);
                    return index;
                }
            return -1;
        }

        static void swap(ref int item1, ref int item2)
        {
            int temp = arr[item1];
            arr[item1] = arr[item2];
            arr[item2] = temp;
        }

 

 

2.二叉查找

数组必须为顺序的

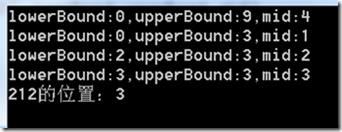
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace 数据结构和算法
{
    class 二叉查找算法
    {
        public readonly static int[] intArr = new int[] { 56, 145, 145, 212, 222, 312, 443, 564, 884, 1212 };

        public static int binSearch(int value)
        {
            int upperBound, lowerBound, mid;
            upperBound = intArr.Length - 1;//最大索引
            lowerBound = 0; //最小索引
            //进入查找状态
            while (lowerBound <= upperBound)
            {
               
                //中间值
                mid = (lowerBound + upperBound) / 2;
                Console.WriteLine(string.Format("lowerBound:{0},upperBound:{1},mid:{2}", lowerBound, upperBound, mid));
                //intArr[mid]中间值
                if (intArr[mid] == value)
                {
                    return mid;
                }
                else
                {
                    //如果value小于中间值intArr[mid]，找前面的一半
                    if (value < intArr[mid])
                    {
                        //中间值之前，最大值为中间值-1
                        //例如
                        upperBound = mid - 1;
                    }
                    else
                    {
                        lowerBound = mid + 1;
                    }
                }
            }
            return -1;
        }

        static void Main()
        {
            Console.WriteLine(("212的位置：" + binSearch(212)));
            Console.ReadKey();
        }
    }
}

 

3.递归二叉查找

同迭代算法相比，递归二叉查找算法的主要问题是它的效率。当用这两种算法对含有 1000 个元素的数组进行排序的时候，递归算法始终比迭代算法慢了 10 倍。

当然，选择递归算法常常是由于效率以外的其他原因，但是应该记住在任何实现递归算法的时候还应该寻找一种迭代的解决方案，这样便于比较两种算法的效率。

 

Array 类所拥有的内置的二叉查找方法

当内置的二叉查找方法与用户定制的方法进行比较的时候，内置方法始终比用户定制方法执行速度快 10 倍。
这没什么好惊讶的。如果按照完全相同的方式使用上述两种方法，那么应该始终优先选择内置的数据结构或算法而非用户定制的。

 

public readonly static int[] intArr = new int[] { 56, 145, 145, 212, 222, 312, 443, 564, 884, 1212 };

 

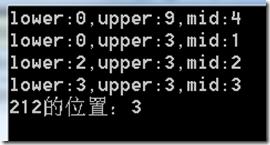
/// <summary>
        /// 递归二叉（二分）查找
        /// </summary>
        /// <param name="value">查找的值</param>
        /// <param name="lower">最小的索引</param>
        /// <param name="upper">最大的索引</param>
        /// <returns></returns>
        public static int RbinSearch(int value, int lower, int upper)
        {

            if (lower > upper)
            {
                return -1;
            }
            else
            {
                int mid = (upper + lower) / 2;
                Console.WriteLine(string.Format("lower:{0},upper:{1},mid:{2}", lower, upper, mid));
                if (value < intArr[mid])
                {
                    return RbinSearch(value, lower, mid - 1);
                }
                else if (value == intArr[mid])
                {
                    return mid;
                }
                else
                {
                    return RbinSearch(value, mid + 1, upper);
                }
            }
        }

        static void Main()
        {
            //Console.WriteLine(("212的位置：" + binSearch(212)));
            Console.WriteLine(("212的位置：" + RbinSearch(212, 0, 9)));
            Console.ReadKey();
        }