树和森林

Posted 2020-10-16 im.lhc

一.树的定义

• 有且仅有一个特点的称为根的节点

• 当n>1时，其余节点可分为m(m>0)个互不相干的有限交集,每个交集称为根的子树。

二.森林的定义

• m个互不相交的森林树的集合，子树的集合称为子树的森林。

三.树的存储结构

1.双亲表示法

• 在树中，除了根节点没有双亲外，其他节点的双亲的唯一确定的。

//双亲存储的结构类型定义
typedef struct PTNode{
  TElemType data; //数据域
  int parent;     //双亲的位置，根节点的双亲为-1
}PTNode;        //双亲的节点类型
typedef struct {
  PTNode *nodes;  //初始化分配的结点数组
  int r,nodeNum; //根的位置和结点数
}PTree;         //树的双亲存储结构类型

优点： 可用parent直接找到双亲，并且很容易找到祖先。

缺点：需要查找节点的孩子及其子孙时要遍历整个结构。

2.双亲孩子表示法

• 是对双亲表示法的扩展，为各节点构造孩子单链表，以便于访问结点的孩子及其子孙，在结点的数组元素中增加firstchild域作为结点的孩子链表头的头指针。

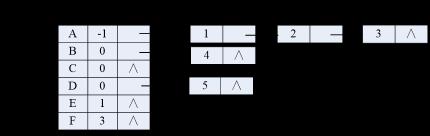
//双亲孩子存储结构的类型定义
typedef struct ChildNode{
  int childIndex;       //孩子在结点数组的位置
  struct ChildNode *nextChild;  //下一个孩子
}ChildNode;         //孩子链表中的节点类型
​
typdef  struct{
  TElemType data;       //元素值
  int parent;           //双亲的位置
  struct ChildNode *firstChild; //孩子链表头指针
}PCTreeNode;            //双亲节点的节点类型
​
typedef struct{
  PCTreeNode *nodes;    //节点数组
  int nodeNum,r;    //结点元素的个数，根位置
}PCTree;            //树的双亲孩子存储结构类型

 

3.孩子兄弟表示法

• 在树中，结点的最左孩子（第一个孩子）和右兄弟如果存在则都是唯一的。采取二叉链式存储结构，每个结点包含三个域，元素值data，最左边孩子指针firstchild和右兄弟指针nextsibling。

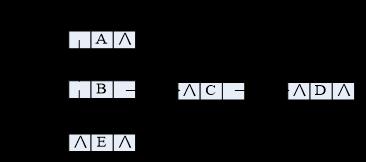
//孩子兄弟链表的类型定义
typedef struct CSTNode{
    TElemType data;         //数据域
    struct CSTNode *firstChild,*nextSibling; //最左孩子指针，右兄弟指针
}CSTnode,*CSTree,*CSForest;     //孩子兄弟链表

 

4.孩子兄弟表示法的树的接口

Status InitTree(CSTree &T); //构造空树
CSTree MakeTree(TElemType e,int n....)  //创建根结点为e和n颗子树的树
Status DestroyTree(CSTree &T)  //销毁树
int TreeDepth(CSTree T)  //返回树的深度
CSNode *Search(CSTree T,TElemType e); //查找树T中的节点e并返回其指针
Status InesertChild(CSTree &T,int i,CSTree c) //插入c为T的第i颗子树，c非空并且与T不相交
Status DeleteChild(CSTree &T,int i) //删除第i棵子树

1.创建树

#include<stdarg.h>// 标准头文件，提供宏va_start、va_arg和va_end，
​
CSTree MakeTree(TElemType e,int n....){
  int i;
  CSTree t,p,pi;
  va_list argptr; //存放变长参数表信息的数组
  t=(CSTree)malloc(sizeof(CSTNode));
  if(t=NULL) return NULL;
  t->data=e;    //根结点的值为e;
  t->firstChild=t->nextSibling=NULL;
  if(n<=0) return t;  //若无子树，则返回根结点
  va_start(argptr,n) //令argptr 指向n后的第一个实参
  p=va_arg(argptr,CSTree); //取第一棵子树的实参转化为CSTree类型
  t->firstChild=p;
  pi=p;
  for(i=1;i<n;i++){
    p=va_arg(argptr,CSTree); //取下一颗子树的实参并转换为CSTree类型
    pi->nextSibling=p;
    pi=p;
  }
  va_end(argptr);
  return t;
}

​
//可变参数的使用
使用可变参数应该有以下步骤（要加入<stdarg.h>): 
​
1)首先在函数里定义一个va_list型的变量,这里是argptr,这个变 量是指向参数的指针. 
​
2)然后用va_start宏初始化变量argptr,这个宏的第二个参数是第一个可变参数的前一个参数,是一个固定的参数. 
​
3)然后用va_arg返回可变的参数,并赋值给变量p(CSTree类型). va_arg的第二个 参数是你要返回的参数的类型,这里是CSTree类型.然后你就可以在函数里使用第二个参数了.如果函数有多个可变参数的,依次调用va_arg获取各个参数. 
​
4)最后用va_end宏结束可变参数的获取.

2.插入第i个子树

Status InesertChild(CSTree &T,int i,CSTree c){
  int j;
  CSTree p;
  if(NULL==T||i<1) return ERROR;
  if(i==1){ //c为第一棵插入子树
    c->nextSibling=T->firstChild;
    T->firstChild=c; //T成为T的第一棵子树
  }else{
    p=T->firstChild;
    for(j=2;p!=NULL&&j<i;j++){
      p=p->nextSibling; //寻找插入位置
    }
    if(j==i){
      c->nextSibling = p->nextSibling;
      p->nextSibling = c;
    }else return ERROR;
  }
  return OK;
}

3.求树的深度

int TreeDepth(CSTree T) {  // 求树T的深度  
    int dep1, dep2, dep;
    if(NULL==T) dep = 0; // 树为空，深度则为0
    else {   
        dep1 = TreeDepth(T->firstChild);    // 求T的子树森林的深度
        dep2 = TreeDepth(T->nextSibling);   // 求除T所在树以外的其余树的深度
        dep = dep1+1>dep2 ? dep1+1 : dep2;  // 树的深度 
     }
     return dep;
} 

4.查找树

CSTreeNode* Search(CSTree T, TElemType e) {  
    // 查找树T中的结点e并返回其指针
    CSTreeNode* result = NULL;       
    if(NULL==T) return NULL;  // 树为空，返回NULL 
    if(T->data==e) return T;  // 找到结点，返回其指针
    if((result = Search(T->firstChild, e))!=NULL) // 在T的子树森林查找
        return result; 
    return Search(T->nextSibling, e); 
        // 在除T所在树以外的其余树构成的森林查找
}
​

 四.树的遍历

1.三种遍历

1.先序(次序)遍历

• 若树不空，则先访问根结点，然后依次先序遍历各棵子树。

2.后序(次序)遍历

• 若树不空，则先依次后序遍历各棵子树，然后访问根结点。

3.层序遍历

• 若树不空，则自上而下自左至右访问树中每个结点。

2.树的先序遍历

若树不为空，则依次进行以下操作：

（1）访问根结点；

（2）访问根结点T所在的子树森林；

（3）除根结点所在树以外的其余树构成的森林。

Status PreOrderTraverseTree(CSTree T, Status(*visit)(TElemType)) {
      if(NULL==T) return OK;//空树
      if(ERROR==visit(T->data)) return ERROR; //访问根节点
      if(ERROR==PreOrderTraverseTree(T->firstChild,visit)) //访问左树
          return ERROR;
      return PreOrderTraverseTree(T->nextSibling,visit);    // 递归访问除T所在树以外的其余树构成的森林
}