二叉搜索树简介

Posted 2020-10-15 dupang

什么是二叉搜索树

　　对于一个任何一个节点x，它的左子树中的关键字最大不超过x.key，其右子树的关键字的值最小不低于x.key。

　　例如下图

　　

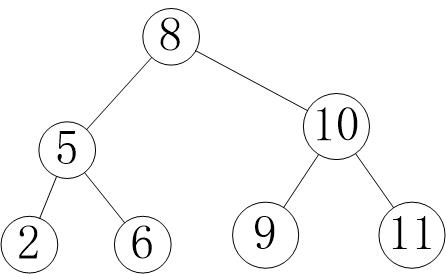
二叉搜索树的遍历

• 　　中序遍历    简单的说就是遍历结果根节点在左子树和右子树之间,先遍历根的左子树，然后遍历根，然后遍历根的右子树，如果左子树或右子树是一个小的树，也是按照先左孩子，根，右孩子的顺序遍历， 例如上图的中序遍历结果是 2,5,6,8,9,10,11
• 　　前序遍历    简单的说就是遍历结果根节点在左子树和右子树前端，先遍历根，然后遍历根的左子树，然后遍历根的右子树，如果左子树或右子树是一个小的树，也是按照先根，左孩子，右孩子的顺序遍历， 例如上图的中序遍历结果是 8,5,2,6,10,9,11
• 　　后序遍历    简单的说就是遍历结果根节点在左子树和右子树后端，先遍历根的左子树，然后遍历根的右子树，最后遍历根，如果左子树或右子树是一个小的树，也是按照先左孩子，右孩子，根的顺序遍历，例如上图的中序遍历结果是 11,9,10,6,2,5,8

二叉搜索树的查询

• 查询 指定一个值，在一棵二叉树中查找对应的节点。
• 最小值 从根节点开始，一直沿着节点的left节点往下走，直到遇到NIL,这时找到节点就是
• 最大值 从根节点开始，一直沉着节点的right节点往下走，走到遇到NIL，这时找到的节点就是
• 前驱 一个节点的前驱是小于这个节点中的最大值的节点。
• 后继 一个节点的后继是大于这个节点中的最小值的节点，

 

二叉搜索树的插入和删除

• 插入   插入操作相对来说比较简单，只要比较节点大小，如果插入的值，大于根节点，就比较根节点的右孩子，如果小于根节点，就比较根节点的左孩子，如此递归。最终会找到要插入的位置。
• 删除

　　　删除比较复杂一点，我们分三种情况来处理，例如一棵树T中要删除的节点的为z。

1. 如果z没有孩子节点，那么只要简单地将它删除，并修改它的父结点，
2. 如果z只有一个孩子，那么将这个孩子移到z的位置上，并修改z的父结点，用z的孩子来替换z。
3. 如果z有两个孩子，那么找z的后继y,并让y移到z的位置。z的原来右子树部分成为y的新的右子树，并且z的左子树成为y的新的左子树。这情况还与y是否为z的右孩子相关。
   1. 如果y是z的右孩子，那么用y替换z,并公留下y的右孩子。
   2. 否则，y位于z的右子树中但并不是z的右孩子。这种情况下，先用y的右孩子替换y,然后再用y替换z。这种情况，就相当于删除了y,因为这种情况下的y不可能有两个孩子，所以问题就又变为1或2的情况了。　　　　

　　　　

 下面是以上操作的JAVA版本提实现 。

 

1 代表树节点的类

/**
 * Created by dupang on 2017/11/12.
 */
public class TreeNode<T> {

    /**
     * 节点的左孩子
     */
    private TreeNode<T> left;
    /**
     * 节点的右孩子
     */
    private TreeNode<T> right;
    /**
     * 节点的父亲
     */
    private TreeNode<T> parent;
    /**
     * 节点的值
     */
    private T value;

    public TreeNode(){

    }
    public TreeNode(TreeNode<T> left,TreeNode<T> right,TreeNode<T> parent,T value){
        this.left=left;
        this.right=right;
        this.parent=parent;
        this.value=value;
    }

    public TreeNode<T> getLeft() {
        return left;
    }

    public void setLeft(TreeNode<T> left) {
        this.left = left;
    }

    public TreeNode<T> getRight() {
        return right;
    }

    public void setRight(TreeNode<T> right) {
        this.right = right;
    }

    public TreeNode<T> getParent() {
        return parent;
    }

    public void setParent(TreeNode<T> parent) {
        this.parent = parent;
    }

    public T getValue() {
        return value;
    }

    public void setValue(T value) {
        this.value = value;
    }
}

 

 2 各个操作测试类

/**
 * Created by dupang on 2017/11/12.
 */
public class SearchTreeTest {
    public static void main(String[] args) {
        int[] values = new int[]{18,5,3,9,2,13,32};
        //初始化一个表示树的根节点
        TreeNode<Integer> root = new TreeNode<>(null,null,null,null);

        //遍历插入
        for (Integer value:values){
            //初始化要插入的节点
            TreeNode<Integer> treeNode = new TreeNode<>(null,null,null,value);
            insert(root,treeNode);
        }

        //中序遍历
        inOrderTreeWalk(root);
        System.out.println();
        //先序遍历
        preOrderTreeWalk(root);
        System.out.println();
        //后序遍历
        postOrderTreeWalk(root);
        System.out.println();

        TreeNode<Integer> treeNode = treeSearch(root,3);
        //求最大值
        treeMaximum(root);
        //求最小值
        treeMinimum(root);
        //后继
        treeSuccessor(root);
        //前驱
        treeSuccessor(root);
    }

    /**
     * 二叉搜索树的插入操作
     * @param root 二叉树的根
     * @param tTreeNode 要插入的节点
     */
    public static void insert(TreeNode<Integer> root,TreeNode<Integer> tTreeNode){
        //声明一个y，用于记录while循环中循环节点的位置，也就是插入节点要插入的位置
        TreeNode<Integer> y = null;
        //把树的根节点赋值给x,先从根节点开始寻找插入的点。
        TreeNode<Integer> x = root;
        while (x!=null&&x.getValue()!=null){
            y=x;
            //如果要插入的值比根节点的值大，
            if(tTreeNode.getValue()>x.getValue()){
                x = x.getRight();
            }else {
                x= x.getLeft();
            }
        }
        //如果y是null，说明是个空树
        if(y==null){
            root.setParent(null);
            root.setLeft(null);
            root.setRight(null);
            root.setValue(tTreeNode.getValue());
        }else if(tTreeNode.getValue()>y.getValue()){
            y.setRight(tTreeNode);
            tTreeNode.setParent(y);
        }else {
            y.setLeft(tTreeNode);
            tTreeNode.setParent(y);
        }
    }

    /**
     * 中序遍历
     * @param treeNode 根节点
     */
    public static void inOrderTreeWalk(TreeNode<Integer> treeNode){
        if (treeNode!=null&&treeNode.getValue()!=null){
            inOrderTreeWalk(treeNode.getLeft());
            System.out.print(treeNode.getValue()+" ");
            inOrderTreeWalk(treeNode.getRight());
        }
    }
    /**
     * 前序遍历
     * @param treeNode 根节点
     */
    public static void preOrderTreeWalk(TreeNode<Integer> treeNode){
        if (treeNode!=null&&treeNode.getValue()!=null){
            System.out.print(treeNode.getValue()+" ");
            inOrderTreeWalk(treeNode.getLeft());
            inOrderTreeWalk(treeNode.getRight());
        }
    }
    /**
     * 后序遍历
     * @param treeNode 根节点
     */
    public static void postOrderTreeWalk(TreeNode<Integer> treeNode){
        if (treeNode!=null&&treeNode.getValue()!=null){
            inOrderTreeWalk(treeNode.getLeft());
            inOrderTreeWalk(treeNode.getRight());
            System.out.print(treeNode.getValue()+" ");
        }
    }

    /**
     * 在树中查询指定值的节点
     * @param treeNode 树的节点
     * @param k 要查询的值
     * @return 如果查询到节点的值等于要查询的值，就返回这个节点，否则返回null
     */
    public static TreeNode<Integer> treeSearch(TreeNode<Integer> treeNode,Integer k){
        if(treeNode==null||treeNode.getValue()==null||treeNode.getValue()==k){
            return treeNode;
        }
        if(k>treeNode.getValue()){
            return treeSearch(treeNode.getRight(),k);
        }else {
            return treeSearch(treeNode.getLeft(),k);
        }
    }

    /**
     * 在树中找到最大值
     * @param treeNode 树的节点
     * @return 如果查询到节点的值等于要查询的值，就返回这个节点，否则返回null
     */
    public static TreeNode<Integer> treeMaximum(TreeNode<Integer> treeNode){
        while (treeNode.getRight()!=null){
            treeNode = treeNode.getRight();
        }
        return treeNode;
    }

    /**
     * 在树中找到最小值
     * @param treeNode 树的节点
     * @return 如果查询到节点的值等于要查询的值，就返回这个节点，否则返回null
     */
    public static TreeNode<Integer> treeMinimum(TreeNode<Integer> treeNode){
        while (treeNode.getLeft()!=null){
            treeNode = treeNode.getLeft();
        }
        return treeNode;
    }

    /**
     * 找一个节点的后继
     * @return 一个节点的后继
     */
    public static TreeNode<Integer> treeSuccessor(TreeNode<Integer> treeNode){
        if(treeNode.getRight()!=null){
            return treeMinimum(treeNode.getRight());
        }
        TreeNode<Integer> y = treeNode.getParent();
        while (y!=null && treeNode==y.getRight()){
            treeNode = y;
            y = y.getParent();
        }
        return y;
    }
    /**
     * 找一个节点的前驱
     * @return 一个节点的前驱
     */
    public static TreeNode<Integer> treePredecessor(TreeNode<Integer> treeNode){
        if(treeNode.getLeft()!=null){
            return treeMaximum(treeNode.getLeft());
        }
        TreeNode<Integer> y = treeNode.getParent();
        while (y!=null && treeNode==y.getLeft()){
            treeNode = y;
            y = y.getParent();
        }
        return y;
    }

    public static void transplant(TreeNode<Integer> root,TreeNode<Integer> target,TreeNode<Integer> source){
        if(target.getParent()==null){
            root.setValue(source.getValue());
            root.setLeft(source.getLeft());
            root.setRight(source.getRight());
            root.setParent(source.getParent());
        }else if(target == target.getParent().getLeft()){
            target.getParent().setLeft(source);
        }else {
            target.getParent().setRight(source);
        }
        source.setParent(target.getParent());
    }

    /**
     * 从一棵树中删除一个节点
     * @param root 根节点
     * @param delete 要删除的节点
     */
    public void treeDelete(TreeNode<Integer> root ,TreeNode<Integer> delete){
        if(delete.getLeft()==null){
            transplant(root,delete,delete.getRight());
        }else if(delete.getRight()==null){
            transplant(root,delete,delete.getLeft());
        }else {
            TreeNode<Integer> y = treeMinimum(delete.getRight());
            if(y.getParent()!=delete){
                transplant(root,y,y.getRight());
                y.setRight(delete.getRight());
                y.getRight().setParent(y);
            }
            transplant(root,delete,y);
            y.setLeft(delete.getLeft());
            y.getLeft().setParent(y);
        }
    }
}