前言
在我们构建完机器学习模型,经常会遇到训练得到模型无法正确预测,这之后我们往往会采取下面的一些方案:
- 增加训练数据
- 减少特征的个数
- 增加更多的特征
- 增加多项式特征(X1*X2 ...)
- 增大lambda的值
- 减小lambda的值
若是不了解模型具体的问题所在,而根据随便拿出一个方案去试错,这往往都是既费力又费心,往往个把月过去了仍然在进行模型的调试。
CV 数据集 [数据集处理]
将一个数据集先按下面进行划分:
- Training set: 60%
- Cross validation set: 20%
- Test set: 20%
计算模型误差 [误差计算]
1.线性回归,直接使用代价函数即可,如下:
for i = 1:m
%依次递增的数据量进行训练模型
theta = trainLinearReg(X(1:i,:), y(1:i), lambda);
%train数据集的测试,使用时去除lambda
error_train(i) =linearRegCostFunction(X(1:i,:), y(1:i), theta, 0);
%cv数据集的测试
error_val(i) = linearRegCostFunction(Xval, yval, theta, 0);
end
2.logistic回归,引出0-1错分率:
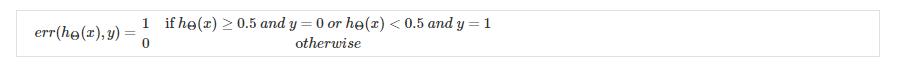
过拟合和欠拟合 [误差分析]
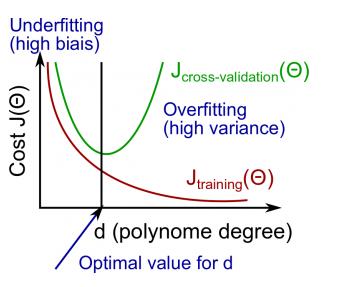
欠拟合:高偏差,Jcv近似于Jtrain。
过拟合:高方差,Jcv远大于Jtrain。
这2个问题是机器学习中最经典的错误情况,很多现象也是由它们一手操办的,来看看下面的3种情况:
样本
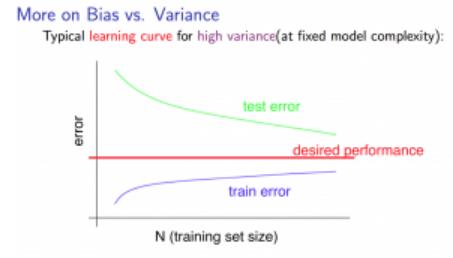
根据上面误差计算部分得来的Training set和cv set得到相应图片
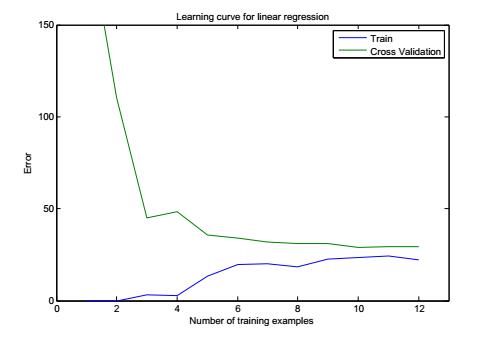
High bias:Jcv与Jtrain非常接近,加入过多样本,对模型的优化没作用
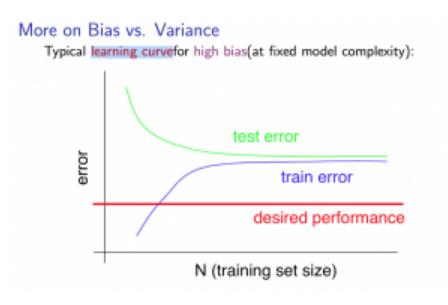
High variance:Jcv远大于Jtrain,增加样本,可以对模型进行优化
多项式特征
多项式特征的选择的多少往往也会给我们带来很大的麻烦,过多的多项式特征会使模型过拟合,而过少的多项式特征会使模型欠拟合。
那么我们该如何进行多项式的选择,下面便引入解决方案:
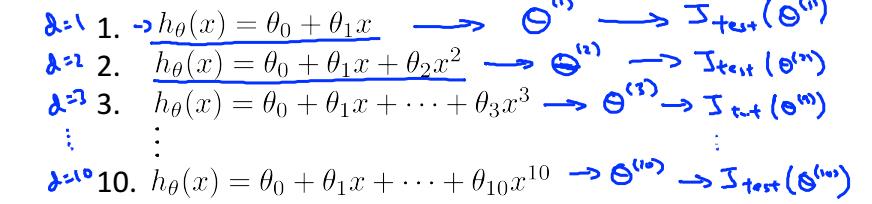
- 使用training set训练每一个多项式,得出相应的theta值。
- 使用cv set获得误差最小的多项式。
- 最后使用test set对多项式进行评估。
lambda
正规化的引入,就是为了防止过拟合,而lambda对拟合程度有着很大影响。若是没有lambda则会出现过拟合现象;而若是lambda过大则会出现欠拟合现象。
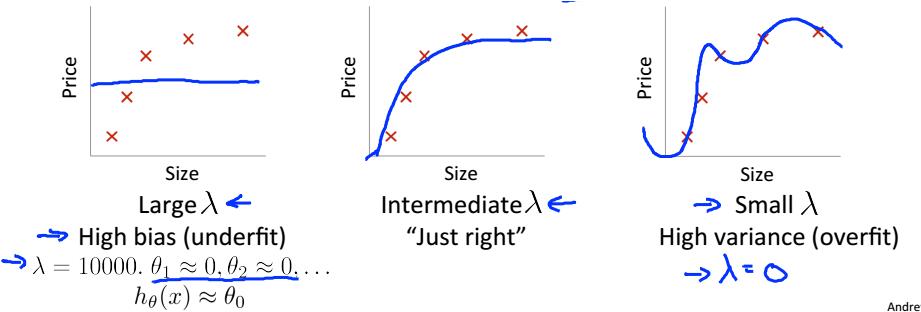
那怎么选择一个较好的lambda呢?
方法类似于多项式特征的选取,稍有不同的就是自己要定义lambda集合。
测试代码段
for i = 1:length(lambda_vec)
lambda = lambda_vec(i);
theta = trainLinearReg(X, y, lambda);
%评估时切记不可在cv set和test set中加入lambda值
error_train(i) = linearRegCostFunction(X, y, theta, 0);
error_val(i) = linearRegCostFunction(Xval, yval, theta, 0);
end
测试结果:
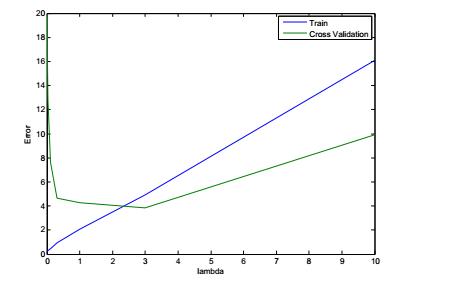
学习曲线
很多情况下因为特征很多,我们往往很难将数据展现出来,而可视化的数据往往给我们的分析带来了很大的帮助;learning curve的绘制无疑是一大助手,learning curve通常是由training set和cv set的误差绘制出来的,中间最重要的就是将training set使用递增的方式进行训练,而cv set则是全部进行使用。如【计算模型误差的代码部分】。