机器学习基本概念解析，机器学习算法概论，机器学习疑难解答，代码分享

Posted 2022-01-02 yk 坤帝

个人公众号 yk 坤帝
后台回复 机器学习解析 获取完整源代码

全文疑难仅代表个人理解，如有差错，不完美的地方，
欢迎各位大佬斧正，感激不尽！！！

1.求解有监督分类问题的一般过程

2.什么是训练集、测试集

3.什么是预测模型

4.什么是损失函数

5.模型训练与模型测试的区别

6.简单房价预测问题

7.Logistic 回归与一般回归方程的区别？

8.朴素贝叶斯数学理论解析

9.机器学习基本算法汇总（附源代码）

9.1 demo06_boston.ipynb 波士顿地区房屋价格预测

利用机器学习进行发票识别

10.demo01-LinearRegression 线性回归算法

1.求解有监督分类问题的一般过程

收集数据集，探索性数据分析，数据预处理，数据分割，利用训练集建立预测模型，选择最佳模型，训练–验证–测试集分割，模型建立，参数调优，模型评价。

2.什么是训练集、测试集

在机器学习模型的开发过程中，希望训练好的模型能在新的、未见过的数据上表现良好。为了模拟新的、未见过的数据，对可用数据进行数据分割，从而将其分割成2部分（有时称为训练—测试分割）。特别是，第一部分是较大的数据子集，用作训练集（如占原始数据的80%），第二部分通常是较小的子集，用作测试集（其余20%的数据）。需要注意的是，这种数据拆分只进行一次。

3.什么是预测模型

利用训练集建立预测模型，然后将这种训练好的模型应用于测试集（即作为新的、未见过的数据）上进行预测。

4.什么是损失函数

用来估量模型的预测值f (x)与真实值Y的不一致程度

5.模型训练与模型测试的区别

模型训练：将训练集数据进行训练，求出预测函数
模型测试：将测试集数据放进预测函数中进行模拟、检验

6.简单房价预测问题

假设房屋价格只与房屋面积有关（x_i表示），价格为y,
求基于一元线性回归的预测模型？
求基于均方误差的损失函数？
求解回归模型的参数？

基于一元线性回归的预测模型： yi=wxi+ b
基于均方误差的损失函数：

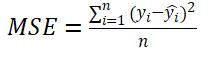
回归模型的参数：

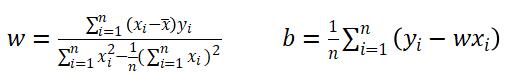
7.Logistic 回归与一般回归方程的区别？

与预测模型的区别？
与损失函数的区别？
与应用场景的区别？

7.1与预测模型的区别

预测模型
线性回归：一般用向量形式表示 f(x)，即

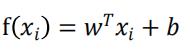
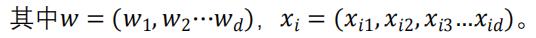
Logistic 回归：

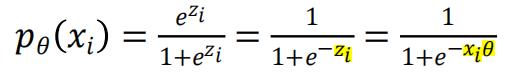
当p0(xi)<0.5时，即zi<0时，则令yi=0(预测为负)
当p0(xi)>0.5时，即zi>0时，则令yi=0(预测为正)
p0(xi)值越小分类为0（负）概率越高，反之分类为1（正）概率越大。

7.2与损失函数的区别

线性回归：线性回归是连续的，所以可以使用MSE来定义损失函数。

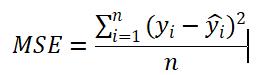
Logistic回归：逻辑回归不是连续的，线性回归损失函数定义的经验无法使用。可以用最大似然法来推导出损失函数，

7.3与应用场景的区别

线性回归模型的先决条件是所有的变量都是连续变量，随着自变量 x 的增加，因变量 y 也 会增加；Logistic 回归适合当因变量为离散变量时，拟合出 x 与 y 的关系。

8.朴素贝叶斯数学理论解析

使用朴素贝叶斯方法，预测x=2,𝑆对应的类别标签（y）

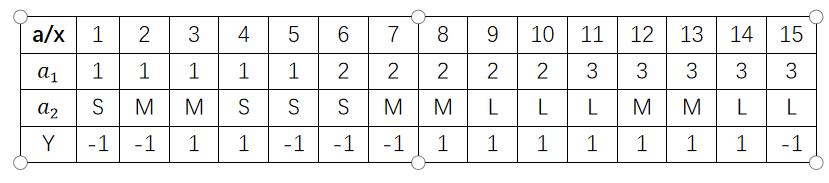
解答过程，需要一定的数学基础：

9.机器学习基本算法汇总（附源代码）

9.1 demo06_boston.ipynb 波士顿地区房屋价格预测
问题六简单房价预测问题的代码部分：

个人公众号 yk 坤帝 
后台回复 机器学习解析  获取完整源代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt


import sklearn.datasets as sd 
boston = sd.load_boston()
#boston.keys()
print(boston.DESCR)

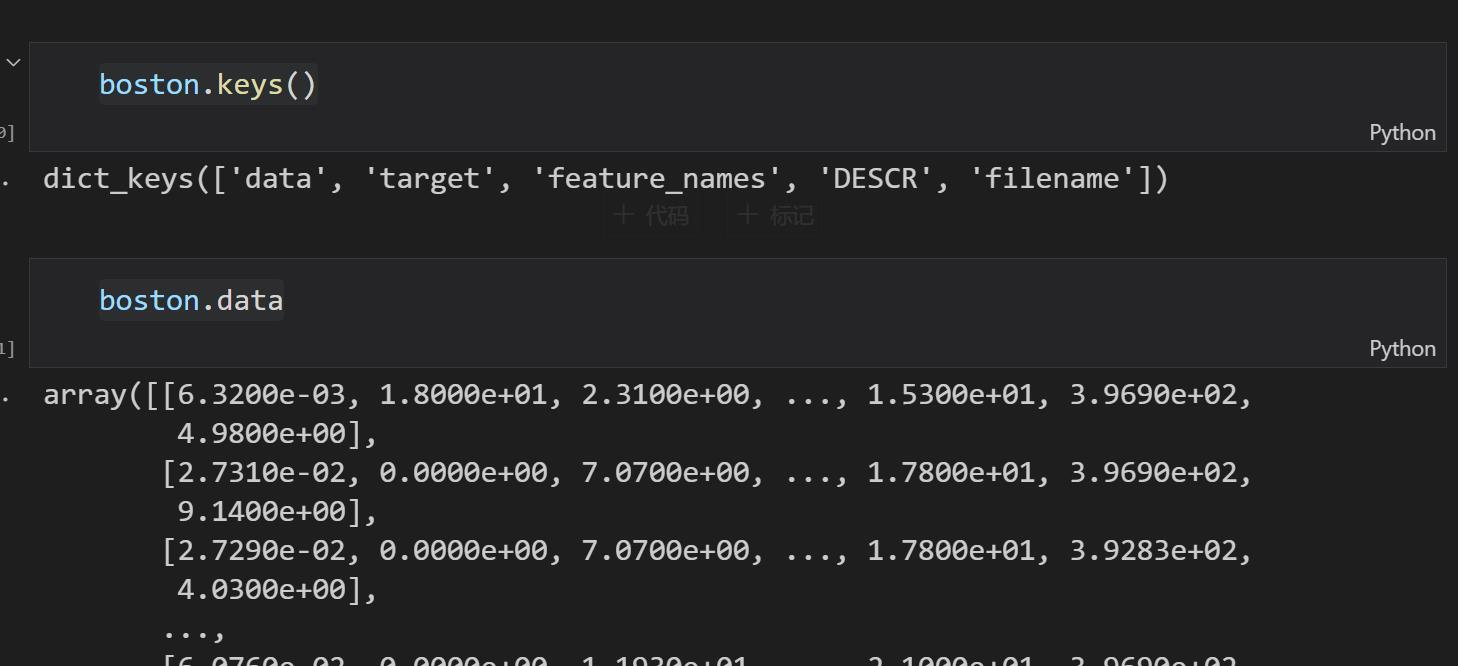
boston.keys()
boston.data
boston.data.shape,boston.target

boston.data.shape,boston.target.shape
boston.data[0],boston.target[0]


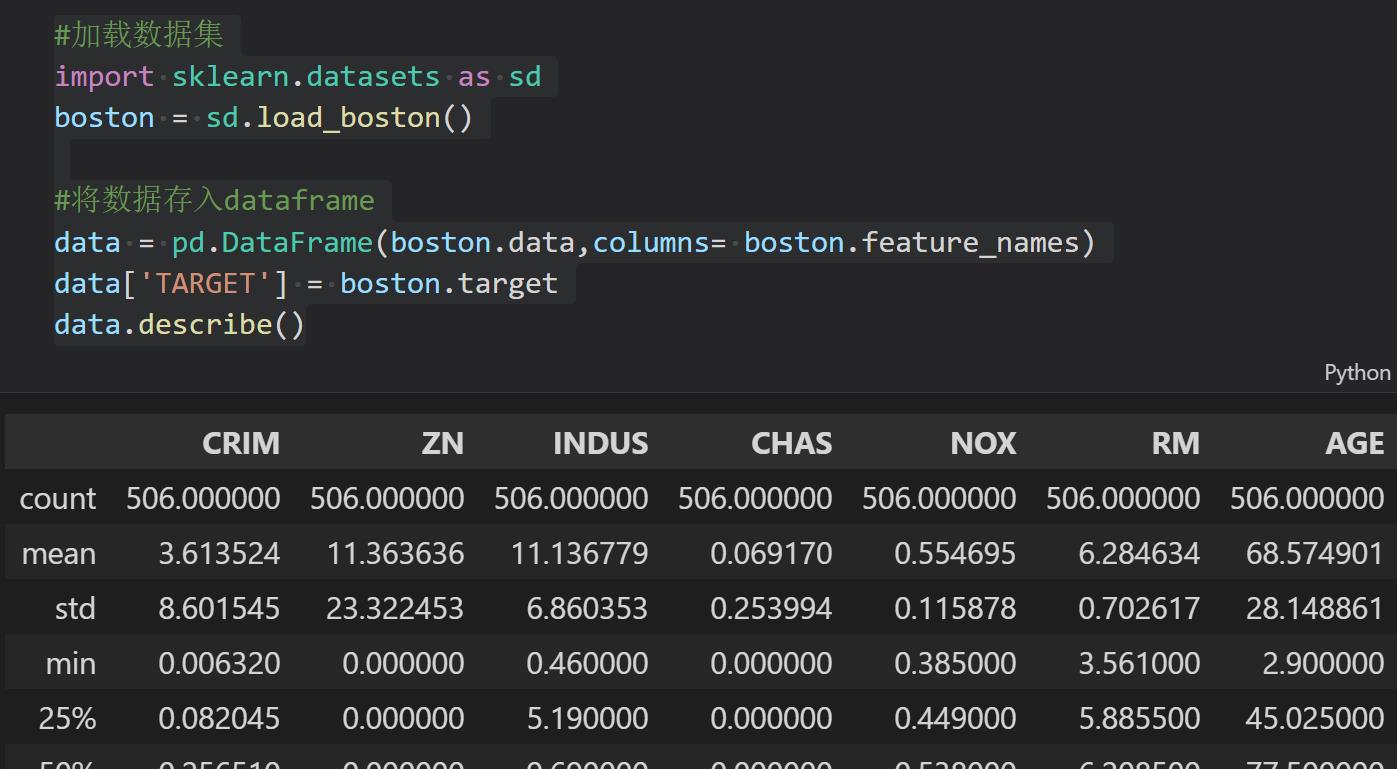
#加载数据集
import sklearn.datasets as sd
boston = sd.load_boston()

#将数据存入dataframe
data = pd.DataFrame(boston.data,columns= boston.feature_names)
data['TARGET'] = boston.target
data.describe()

#对某些字段进行简单的数据分析
data.pivot_table(index = 'CHAS',values = ['TARGET'])


#如果想使用这组数据训练线性模型，则要先验证特征与输出的关系是否是线性关系
data.plot.scatter(x = 'RM', y = 'TARGET')

data.plot.scatter(x = 'DIS', y = 'TARGET')

data.plot.scatter(x = 'PTRATIO', y = 'TARGET')

plt.scatter(x = data['PTRATIO'], y = data['TARGET'])

import sklearn.model_selection as ms 
import sklearn.metrics as sm 
import sklearn.linear_model as lm

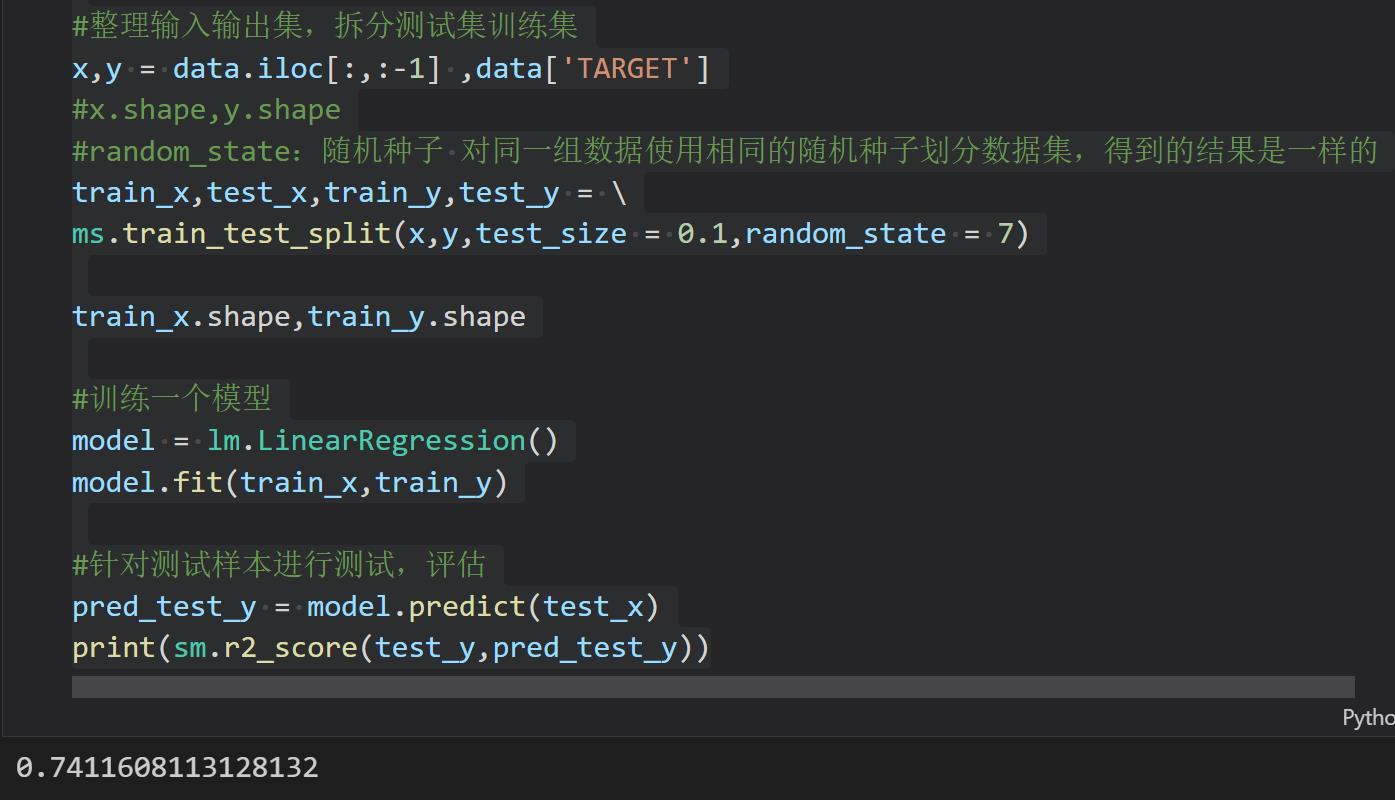
#整理输入输出集，拆分测试集训练集
x,y = data.iloc[:,:-1] ,data['TARGET']
#x.shape,y.shape
#random_state：随机种子 对同一组数据使用相同的随机种子划分数据集，得到的结果是一样的
train_x,test_x,train_y,test_y = \\
ms.train_test_split(x,y,test_size = 0.1,random_state = 7)

train_x.shape,train_y.shape

#训练一个模型
model = lm.LinearRegression()
model.fit(train_x,train_y)

#针对测试样本进行测试，评估
pred_test_y = model.predict(test_x)
print(sm.r2_score(test_y,pred_test_y))

10.demo01-LinearRegression 线性回归算法

个人公众号 yk 坤帝 
后台回复 机器学习解析  获取完整源代码

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd 

x = np.array([0.5, 0.6,0.8,1.1,1.4])
y = np.array([5.0,5.5,6.0,6.8,7.0])

#加载数据集
data = pd.read_csv('qq邮箱.csv')
#data
x = data['YearsExperience']
y = data['Salary']

plt.grid(linewidth = 2)
plt.scatter(x,y,s = 60,color = 'dodgerblue' ,label = 'Samples')

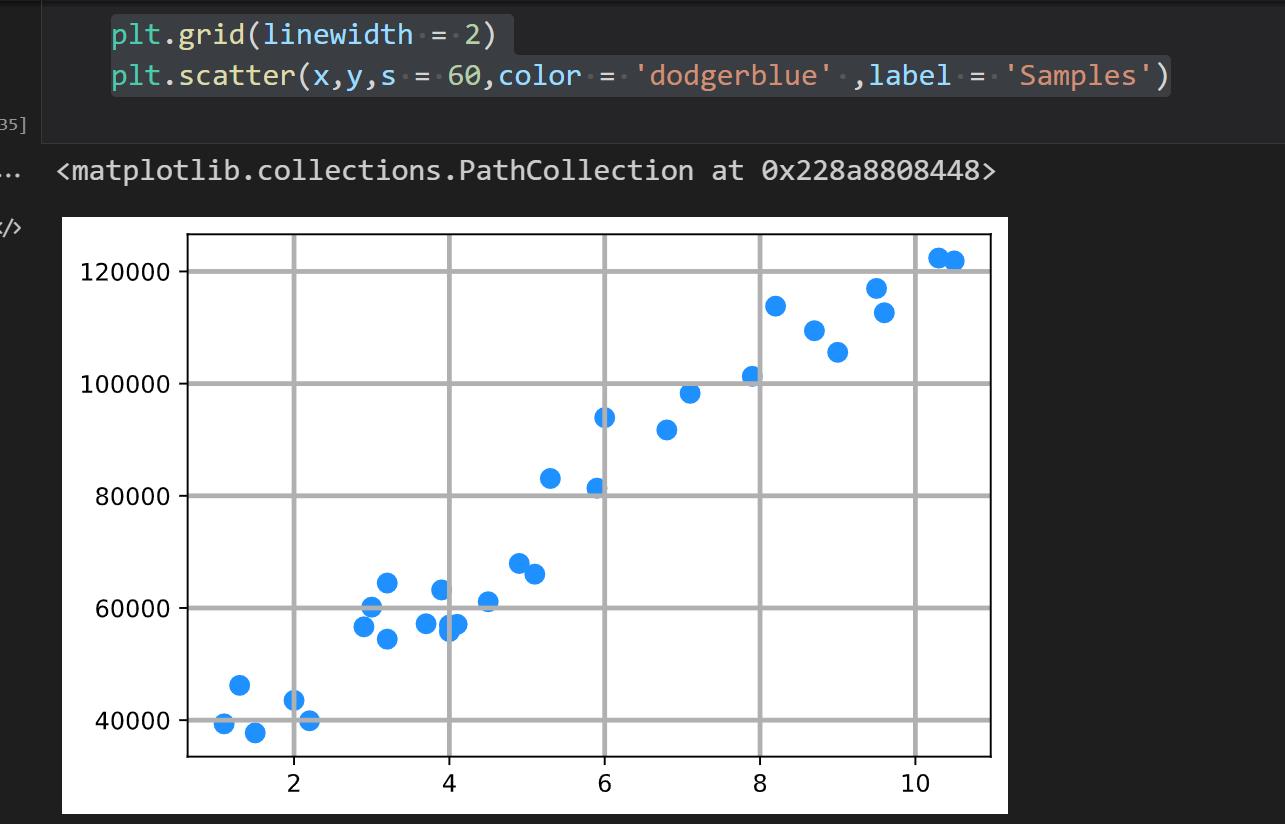
基于梯度下降算法，不断更新w0与w1，从而找到最佳的模型参数

个人公众号 yk 坤帝 
后台回复 机器学习解析  获取完整源代码

# x = np.array([0.5, 0.6,0.8,1.1,1.4])
# y = np.array([5.0,5.5,6.0,6.8,7.0])

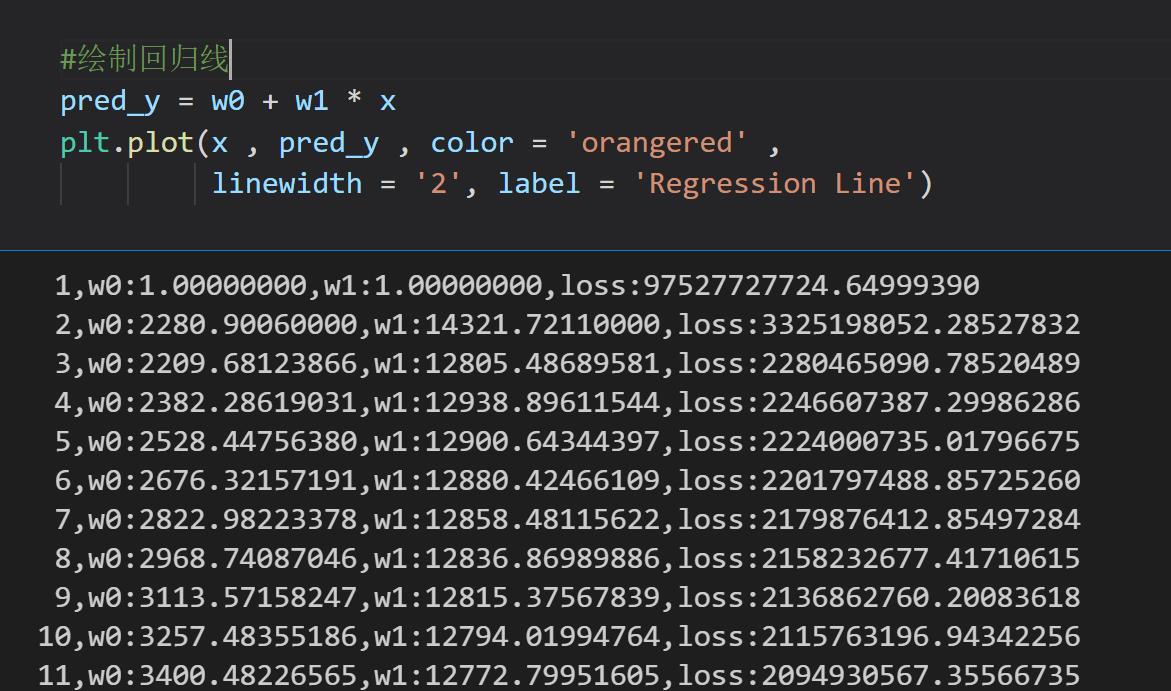
#基于梯度下降算法，不断更新w0与w1，从而找到最佳的模型参数
w0,w1,lrate = 1,1,0.001
times = 600

w0s,w1s,losses,epoches = [],[],[],[]

for i in range(times):
    #输出每一轮运算过程中，w0，w1，loss的变化过程
    loss = 1/2 * ((w0 + w1*x - y)**2).sum()
    print(':4,w0::.8f,w1::.8f,loss::.8f'.format(i+1,w0,w1,loss))

    epoches.append(i+1)
    w0s.append(w0)
    w1s.append(w1)
    losses.append(loss)

    #计算w0与w1方向上的偏导数，代入模型参数的更新公式
    d0 = (w0 + w1*x - y).sum()
    d1 = (x*(w0 + w1*x - y)).sum()

    w0 = w0 - lrate*d0
    w1 = w1 - lrate*d1
w0,w1  #(截距，斜率)

#绘制样本点
plt.grid(linestyle = ':')
plt.scatter(x,y,s = 60,color = 'dodgerblue' ,label = 'Samples')

#绘制回归线
pred_y = w0 + w1 * x
plt.plot(x , pred_y , color = 'orangered' ,
         linewidth = '2', label = 'Regression Line')

plt.subplot(3,1,1)
plt.grid(linestyle = ':')
plt.ylabel('w0')
plt.plot(epoches,w0s,color = 'dodgerblue',label = 'w0')
plt.legend()

plt.subplot(3,1,2)
plt.grid(linestyle = ':')
plt.ylabel('w1')
plt.plot(epoches,w1s,color = 'dodgerblue',label = 'w1')
plt.legend()

plt.subplot(3,1,3)
plt.grid(linestyle = ':')
plt.ylabel('loss')
plt.plot(epoches,losses,color = 'orangered',label = 'loss')
plt.legend()

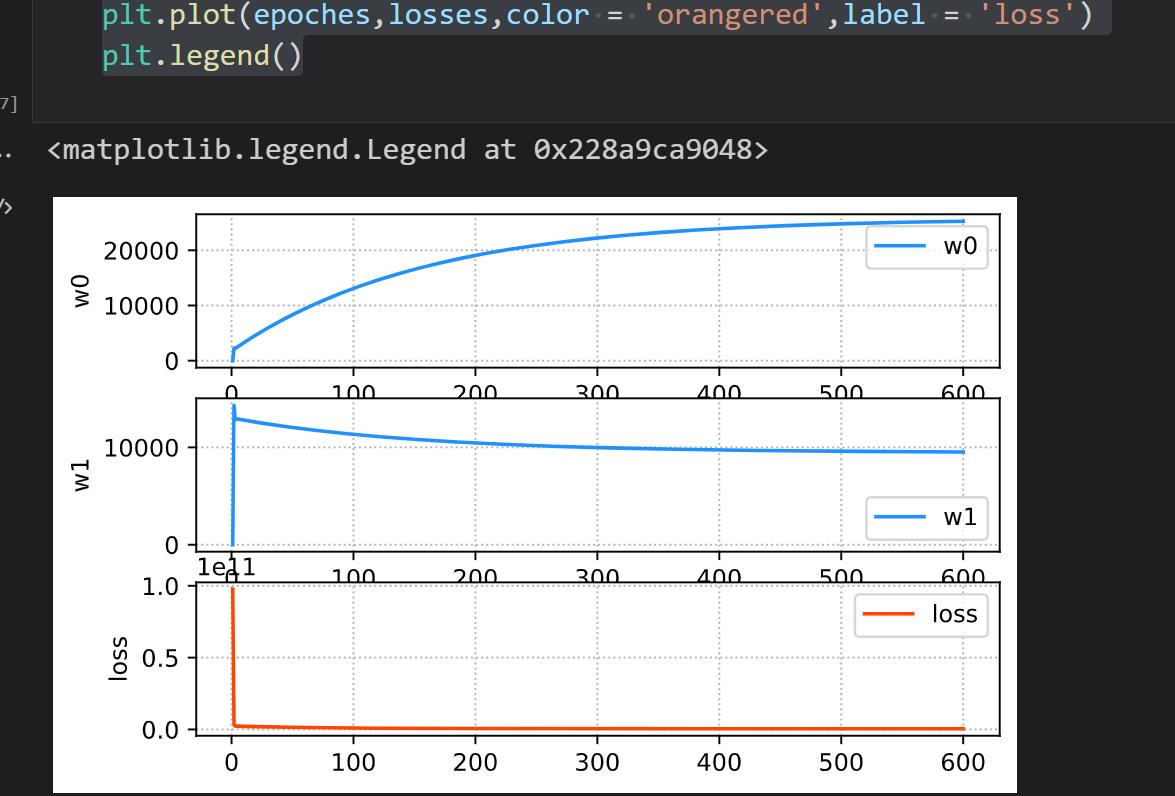
plt.subplot(3,1,1)
plt.grid(linestyle = ':')
plt.ylabel('w0')
plt.plot(epoches,w0s,color = 'dodgerblue',label = 'w0')
plt.legend()

plt.xticks([])

plt.subplot(3,1,2)
plt.grid(linestyle = ':')
plt.ylabel('w1')
plt.plot(epoches,w1s,color = 'dodgerblue',label = 'w1')
plt.legend()

plt.xticks([])

plt.subplot(3,1,3)
plt.grid(linestyle = ':')
plt.ylabel('loss')
plt.plot(epoches,losses,color = 'orangered',label = 'loss')
plt.legend()

全文疑难仅代表个人理解，如有差错，不完美的地方，
欢迎各位大佬斧正，感激不尽！！！

个人公众号 yk 坤帝
后台回复 机器学习解析 获取完整源代码