机器学习之朴素贝叶斯算法
Posted 追寻的鹿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习之朴素贝叶斯算法相关的知识,希望对你有一定的参考价值。
声明:本篇博文是学习《机器学习实战》一书的方式路程,系原创,若转载请标明来源。
1 贝叶斯定理的引入
概率论中的经典条件概率公式:

公式的理解为,P(X ,Y)= P(Y,X)<=> P(X | Y)P(Y)= P(Y | X)P (X),即 X 和 Y 同时发生的概率与 Y 和 X 同时发生的概率一样。
2 朴素贝叶斯定理
朴素贝叶斯的经典应用是对垃圾邮件的过滤,是对文本格式的数据进行处理,因此这里以此为背景讲解朴素贝叶斯定理。设D 是训练样本和相关联的类标号的集合,其中训练样本的属性集为 X { X1,X2, ... , Xn }, 共有n 个属性;类标号为 C{ C1,C2, ... ,Cm }, 有m 中类别。朴素贝叶斯定理:
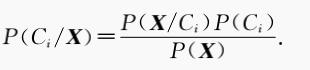
其中,P(Ci | X)为后验概率,P(Ci)为先验概率,P(X | Ci)为条件概率。朴素贝叶斯的两个假设:1、属性之间相互独立。2、每个属性同等重要。通过假设1 知,条件概率P(X | Ci)可以简化为:

3 朴素贝叶斯算法
朴素贝叶斯算法的核心思想:选择具有最高后验概率作为确定类别的指标。下面是以过滤有侮辱性的评论为例,介绍朴素贝叶斯利用Python 语言实现的过程,其本质是利用词和类别的联合概率来预测给定文档属于某个类别。
4 使用Python对文本分类
4.1 建立文本数据
文本数据用一个个对象组成,一个对象是由若干单词组成,每个对象对应一个确定的类别。
代码如下:
1 # 文本数据集 2 def loadDataList(): 3 postingList = [ 4 [\'my\',\'dog\',\'has\',\'flea\',\'problems\',\'help\',\'please\'], 5 [\'maybe\',\'not\',\'take\',\'him\',\'to\',\'dog\',\'park\',\'stupid\'], 6 [\'my\',\'dalmation\',\'is\',\'so\',\'cute\',\'I\',\'love\',\'him\'], 7 [\'stop\',\'posting\',\'stupid\',\'worthless\',\'garbage\'], 8 [\'mr\',\'licks\',\'ate\',\'my\',\'steak\',\'how\',\'to\',\'stop\',\'him\'], 9 [\'quit\',\'buying\',\'worthless\',\'dog\',\'food\',\'stupid\']] 10 classVec = [0,1,0,1,0,1] 11 return postingList ,classVec
4.2 对文本数据的处理
从文本数据中提取出训练样本的属性集,这里是属性集是由单词组成的词汇集。
代码如下:
1 # 提取训练集的所有词 2 def createVocabList(dataSet): 3 vocabSet = set([]) 4 for document in dataSet : 5 vocabSet = vocabSet | set(document) # 两个集合的并集 6 return list(vocabSet)
这里利用集合的性质对数据集提取不同的单词,函数 createVocabList() 返回值是列表类型。
4.3 对词汇集转化成数值类型
因为单词的字符串类型无法参与到数值的计算,因此把一个对象的数据由词汇集中的哪些单词组成表示成:0 该对象没有这个词,1 该对象有这个词。
代码如下:
1 # 根据类别对词进行划分数值型的类别 2 def setOfWords2Vec(vocabList, inputSet): 3 returnVec = [0]*len(vocabList) 4 for word in inputSet: 5 if word in vocabList: 6 returnVec[vocabList.index(word)] = 1 7 else : 8 print "the word : %s is not in my Vocabulary!" % word 9 return returnVec
参数 vocabList 是词汇集,inputSet 是对象的数据,而返回值是由词汇集的转换成 0 和 1 组成的对象单词在词汇集的标记。
4.4 朴素贝叶斯分类器的训练函数
这里说明一下,训练样本是postingList 列表数据,属性集是词汇集,类标号是classVec 列表数据。在编写代码时考虑到对象的单词在词汇集中占有率比较低,会造成词汇集转化时有大量的 0 组成,同时又会造成条件概率大量为 0 ;又有计算真实概率值普遍偏小,容易造成下溢出。因此,代码对计算条件概率时进行转换,但不影响条件概率的大小排序,也就不会影响朴素贝叶斯的使用。
代码如下:
1 \'\'\' 2 求贝叶斯公式中的先验概率 pAbusive ,条件概率 p0Vect、p1Vect;函数中所求的概率值 3 是变形值,不影响贝叶斯的核心思想:选择具有最高概率的决策 4 \'\'\' 5 def trainNB0(trainMatrix, trainCategory): 6 numTrainDocs = len(trainMatrix) # 样本中对象的个数 7 numWords = len(trainMatrix[0]) # 样本中所有词的集合个数 8 pAbusive = sum(trainCategory) / float(numTrainDocs) # 对类别只有两种的先验概率计算 9 # 对所有词在不同的类别下出现次数的初始化为1,为了防止计算条件概率出现为0 10 p0Num = ones(numWords) 11 p1Num = ones(numWords) 12 # 对不同类别出现次数的初始化为2,词的出现数初始数为1的情况下,增加分母值避免概率值大于1 13 p0Denom = 2.0 14 p1Denom = 2.0 15 for i in range(numTrainDocs): # 遍历所有对象 16 if trainCategory[i] == 1: # 类别类型的判断 17 p1Num += trainMatrix[i] # 对所有词在不同的类别下出现次数的计算 18 p1Denom += sum(trainMatrix[i]) # 对不同类别出现次数的计算 19 else: 20 p0Num += trainMatrix[i] # 对所有词在不同的类别下出现次数的计算 21 p0Denom += sum(trainMatrix[i]) # 对不同类别出现次数的计算 22 p1Vect = log ( p1Num / p1Denom) # 条件概率,用对数的形式计算是为避免概率值太小造成下溢出 23 p0Vect = log (p0Num / p0Denom) # 条件概率,用对数的形式计算是为避免概率值太小造成下溢出 24 return p0Vect, p1Vect, pAbusive
4.5 朴素贝叶斯的分类函数
根据先验概率和条件概率对不同类别的后验概率进行计算,并选取后验概率最大的类别作为朴素贝叶斯预测结果值。
代码如下:
1 # 计算后验概率,并选择最高概率作为预测类别 2 def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1): 3 p1 = sum(vec2Classify * p1Vec ) + log(pClass1) # 对未知对象的单词的每一项的条件概率相加(对数相加为条件概率的相乘) 4 p0 = sum(vec2Classify * p0Vec ) + log(1.0-pClass1 ) # 后面加上的一项是先验概率 5 if p1 > p0: 6 return 1 7 else : 8 return 0
4.6 测试样本的预测
通过朴素贝叶斯算法给出两个未知类别的对象预测其类别。
代码如下:
1 # 对侮辱性语言的测试 2 def testingNB(): 3 listOposts, listClasses = loadDataList() # 训练样本的数据,listOposts 为样本,listClasses 为样本的类别 4 myVocabList = createVocabList(listOposts ) # 样本的词汇集 5 trainMat = [] # 对样本的所有对象相关的单词转化为数值 6 for postinDoc in listOposts : 7 trainMat.append(setOfWords2Vec(myVocabList ,postinDoc ) ) 8 p0V, p1V, pAb = trainNB0(array(trainMat),array(listClasses)) # 样本的先验概率和条件概率 9 10 testEntry = [\'love\',\'my\',\'dalmation\',\'love\'] # 未知类别的对象 11 thisDoc = array(setOfWords2Vec(myVocabList ,testEntry ) ) # 对未知对象的单词转化为数值 12 print testEntry ,\'classified as : \',classifyNB(thisDoc, p0V,p1V,pAb) # 对未知对象的预测其类别 13 14 testEntry = [\'stupid\',\'garbage\'] # 未知类别的对象 15 thisDoc = array(setOfWords2Vec(myVocabList ,testEntry )) # 对未知对象的单词转化为数值 16 print testEntry, \'classified as : \', classifyNB(thisDoc, p0V, p1V, pAb) # 对未知对象的预测其类别
其运行结果图:

对象 [\'love\',\'my\',\'dalmation\',\'love\'] 由直观可知,其类别是非侮辱性词汇,与预测结果(0 代表正常语言)相同;对象 [\'stupid\',\'garbage\'] 类别是侮辱性词汇,与预测结果(1 代表侮辱性语言)相同,说明朴素贝叶斯算法对预测类别有效。
5 例子:对垃圾邮件的识别
这里给出朴素贝叶斯算法最经典的应用实例,对垃圾邮件的过滤识别。由于邮件是以文件的形式保存,因此我们要对邮件的内容进行提取并处理成符合算法可用的类型。
5.1 邮件文件解析
利用正则语言对邮件的内容进行单词的划分。
代码如下:
1 # 邮件文件解析 2 def textParse(bigString): 3 import re 4 listOfTokens = re.split(r\'\\w*\', bigString) # 利用正则语言对邮件文本进行解析 5 return [tok.lower() for tok in listOfTokens if len(tok) > 2] # 限定单词的字母大于2
第5 行代码解释: lower() 方法转换字符串中所有大写字符为小写
5.2 垃圾邮件测试函数
代码如下
1 # 完整的垃圾邮件测试函数 2 def spamTest(): 3 docList=[];classList = []; fullText = [] 4 for i in range(1,26): 5 wordList = textParse(open(\'email/spam/%d.txt\' %i ).read()) 6 docList.append(wordList) # 把解析后的邮件作为训练样本 7 fullText.extend(wordList) 8 classList.append(1) # 邮件所对应的类别 9 wordList = textParse(open(\'email/ham/%d.txt\' % i).read()) 10 docList.append(wordList) # 把解析后的邮件作为训练样本 11 fullText.extend(wordList ) 12 classList .append(0) # 邮件所对应的类别 13 vocabList = createVocabList(docList) # 样本生成的词汇集 14 # 随机产生十个测试样本和四十个训练样本 15 trainingSet = range(50);testSet = [] 16 for i in range(10): 17 randIndex = int (random.uniform(0,len(trainingSet ))) 18 testSet.append(trainingSet [randIndex ]) 19 del[trainingSet[randIndex]] 20 # 对训练样本进行词的转化成数值类型 21 trainMat = [] 22 trainClasses = [] 23 for docIndex in trainingSet : 24 trainMat.append(setOfWords2Vec(vocabList, docList [docIndex ]) ) 25 trainClasses.append(classList[docIndex ]) 26 p0V, p1V, pSpam = trainNB0(array(trainMat), array(trainClasses)) # 训练样本的先验概率及条件概率 27 errorCount = 0 # 测试样本的出错数初始化 28 for docIndex in testSet: 29 wordVector = setOfWords2Vec(vocabList ,docList[docIndex ]) # 测试对象的词的数值转化 30 if classifyNB(array(wordVector), p0V, p1V, pSpam) != classList[docIndex ]: # 预测的类别与真实类别的对比 31 errorCount += 1 32 print \'the error rate is : \', float (errorCount )/ len(testSet) # 测试样本的出错率
第17 行代码解释:
uniform() 函数是在random模块里,将随机生成下一个实数,它在 [x, y) 范围内。
x -- 随机数的最小值,包含该值。
y -- 随机数的最大值,不包含该值。
返回值是一个浮点数
运行结果图

结果显示测试集的出错比例是10%,由于训练集是随机组合的,因此每次运行的结果会有所不同。在《机器学习实战》一书中给出这个算法的错误率在6%左右,说明朴素贝叶斯算法在严苛的条件下也有较好的效果。严苛条件是指我们对属性都是独立的,这在现实中很难找到符合这样的条件。对垃圾邮件的过滤也是不例外的,如bacon(培根) 出现在unhealthy (不健康的)后面与出现在delicious(美味的)后面的概率是不同的,bacon(培根)常常与delicious (美味的)搭配。
附 完整代码

# -*- coding:utf-8 -*- from numpy import * # 文本数据集 def loadDataList(): postingList = [ [\'my\',\'dog\',\'has\',\'flea\',\'problems\',\'help\',\'please\'], [\'maybe\',\'not\',\'take\',\'him\',\'to\',\'dog\',\'park\',\'stupid\'], [\'my\',\'dalmation\',\'is\',\'so\',\'cute\',\'I\',\'love\',\'him\'], [\'stop\',\'posting\',\'stupid\',\'worthless\',\'garbage\'], [\'mr\',\'licks\',\'ate\',\'my\',\'steak\',\'how\',\'to\',\'stop\',\'him\'], [\'quit\',\'buying\',\'worthless\',\'dog\',\'food\',\'stupid\']] classVec = [0,1,0,1,0,1] return postingList ,classVec # 提取训练集中的所有词 def createVocabList(dataSet): vocabSet = set([]) for document in dataSet : vocabSet = vocabSet | set(document) # 两个集合的并集 return list(vocabSet) # 根据类别对词进行划分数值型的类别 def setOfWords2Vec(vocabList, inputSet): returnVec = [0]*len(vocabList) for word in inputSet: if word in vocabList: returnVec[vocabList.index(word)] = 1 else : print "the word : %s is not in my Vocabulary!" % word return returnVec # 文档词袋模型,可以对重复的单词计数 def bagOfWords2Vec(vocabList, inputSet): returnVec = [0]*len(vocabList) for word in inputSet: if word in vocabList: returnVec[vocabList.index(word)] += 1 return returnVec \'\'\' 求贝叶斯公式中的先验概率 pAbusive ,条件概率 p0Vect、p1Vect;函数中所求的概率值 是变形值,不影响贝叶斯的核心思想:选择具有最高概率的决策 \'\'\' def trainNB0(trainMatrix, trainCategory): numTrainDocs = len(trainMatrix) # 样本中对象的个数 numWords = len(trainMatrix[0]) # 样本中所有词的集合个数 pAbusive = sum(trainCategory) / float(numTrainDocs) # 对类别只有两种的先验概率计算 # 对所有词在不同的类别下出现次数的初始化为1,为了防止计算条件概率出现为0 p0Num = ones(numWords) p1Num = ones(numWords) # 对不同类别出现次数的初始化为2,词的出现数初始数为1的情况下,增加分母值避免概率值大于1 p0Denom = 2.0 p1Denom = 2.0 for i in range(numTrainDocs): # 遍历所有对象 if trainCategory[i] == 1: # 类别类型的判断 p1Num += trainMatrix[i] # 对所有词在不同的类别下出现次数的计算 p1Denom += sum(trainMatrix[i]) # 对不同类别出现次数的计算 else: p0Num += trainMatrix[i] # 对所有词在不同的类别下出现次数的计算 p0Denom += sum(trainMatrix[i]) # 对不同类别出现次数的计算 p1Vect = log ( p1Num / p1Denom) # 条件概率,用对数的形式计算是为避免概率值太小造成下溢出 p0Vect = log (p0Num / p0Denom) # 条件概率,用对数的形式计算是为避免概率值太小造成下溢出 return p0Vect, p1Vect, pAbusive # 计算后验概率,并选择最高概率作为预测类别 def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1): p1 = sum(vec2Classify * p1Vec ) + log(pClass1) # 对未知对象的单词的每一项的条件概率相加(对数相加为条件概率的相乘) p0 = sum(vec2Classify * p0Vec ) + log(1.0-pClass1 ) # 后面加上的一项是先验概率 if p1 > p0: return 1 else : return 0 # 对侮辱性语言的测试 def testingNB(): listOposts, listClasses = loadDataList() # 训练样本的数据,listOposts 为样本,listClasses 为样本的类别 myVocabList = createVocabList(listOposts ) # 样本的词汇集 trainMat = [] # 对样本的所有对象相关的单词转化为数值 for postinDoc in listOposts : trainMat.append(setOfWords2Vec(myVocabList ,postinDoc ) ) p0V, p1V, pAb = trainNB0(array(trainMat),array(listClasses)) # 样本的先验概率和条件概率 testEntry = [\'love\',\'my\',\'dalmation\',\'love\'] # 未知类别的对象 thisDoc = array(setOfWords2Vec(myVocabList ,testEntry ) ) # 对未知对象的单词转化为数值 print testEntry ,\'classified as : \',classifyNB(thisDoc, p0V,p1V,pAb) # 对未知对象的预测其类别 testEntry = [\'stupid\',\'garbage\'] # 未知类别的对象 thisDoc = array(setOfWords2Vec(myVocabList ,testEntry )) # 对未知对象的单词转化为数值 print testEntry, \'classified as : \', classifyNB(thisDoc, p0V, p1V, pAb) # 对未知对象的预测其类别 # 邮件文件解析 def textParse(bigString): import re listOfTokens = re.split(r\'\\w*\', bigString) # 利用正则语言对邮件文本进行解析 return [tok.lower() for tok in listOfTokens if len(tok) > 2] # 限定单词的字母大于2 # 完整的垃圾邮件测试函数 def spamTest(): docList=[];classList = []; fullText = [] for i in range(1,26): wordList = textParse(open(\'email/spam/%d.txt\' %i ).read()) docList.append(wordList) # 把解析后的邮件作为训练样本 fullText.extend(wordList) classList.append(1) # 邮件所对应的类别 wordList = textParse(open(\'email/ham/%d.txt\' % i).read()) docList.append(wordList) # 把解析后的邮件作为训练样本 fullText.extend(wordList ) classList .append(0) # 邮件所对应的类别 vocabList = createVocabList(docList) # 样本生成的词汇集 # 随机产生十个测试样本和四十个训练样本 trainingSet = range(50);testSet = [] for i in range(10): randIndex = int (random.uniform(0,len(trainingSet ))) testSet.append(trainingSet [randIndex ]) del[trainingSet[randIndex]] # 对训练样本进行词的转化成数值类型 trainMat = [] trainClasses = [] for docIndex in trainingSet : trainMat.append(setOfWords2Vec(vocabList, docList [docIndex ]) ) trainClasses.append(classList[docIndex ]) p0V, p1V, pSpam = trainNB0(array(trainMat), array(trainClasses)) # 训练样本的先验概率及条件概率 errorCount = 0 # 测试样本的出错数初始化 for docIndex in testSet: wordVector = setOfWords2Vec(vocabList ,docList[docIndex ]) # 测试对象的词的数值转化 if classifyNB(array(wordVector), p0V, p1V, pSpam) != classList[docIndex ]: # 预测的类别与真实类别的对比 errorCount += 1 print \'the error rate is : \', float (errorCount )/ len(testSet) # 测试样本的出错率 if __name__ == \'__main__\': #testingNB() # 对侮辱性评价的测试 spamTest() # 对垃圾邮件的测试
以上是关于机器学习之朴素贝叶斯算法的主要内容,如果未能解决你的问题,请参考以下文章
