编程之美学习之最长子序列的解法

Posted 2020-10-12

 

　　实在愚钝，虽然是以前看过的算法，今天也是折腾了一天才稍微弄懂了一些。特此记下笔记

　　第一次遇到这个问题的场景是猴子摘桃问题，原题如下：

　　小猴子下山，沿着下山的路有一排桃树，每棵树都结了一些桃子。小猴子想摘桃子，但是有一些条件需要遵守，小猴子只能沿着下山的方向走，
不能回头，每颗树最多摘一个，而且一旦摘了一棵树的桃子，就不能再摘比这棵树结的桃子少的树上的桃子。那么小猴子最多能摘到几颗桃子呢？
举例说明，比如有5棵树，分别结了10，4，5，12，8颗桃子，那么小猴子最多能摘3颗桃子，来自于结了4，5，8颗桃子的桃树

　　首先讲第一种解法：

　　要明白这题最关键的一步就是要清楚，不要直接拿数组中的元素一个个去比较，只需要知道，前 i 个元素中最长的递增子序列（LIS）的长度，或者，以第 i 个元素结尾的LIS的长度 ，第1个元素结尾的LIS的只有他自己一个，所以result[0] = 1，以第2个元素结尾的LIS则之需要和第1个元素peach[0]比较即可，若大于第1个元素，则在result[0]++ 就是他的LIS ，若小于，则同样result[1]=1 ， 很明显，第i个元素结尾的LIS起码都是1。。  以后的任意i值，都可以依次类推获得到结果。 以下是该方法的算法代码：

/*小猴子下山，沿着下山的路有一排桃树，每棵树都结了一些桃子。小猴子想摘桃子，但是有一些条件需要遵守，小猴子只能沿着下山的方向走，
    不能回头，每颗树最多摘一个，而且一旦摘了一棵树的桃子，就不能再摘比这棵树结的桃子少的树上的桃子。那么小猴子最多能摘到几颗桃子呢？
    举例说明，比如有5棵树，分别结了10，4，5，12，8颗桃子，那么小猴子最多能摘3颗桃子，来自于结了4，5，8颗桃子的桃树。*/
    int peaches[] = null;
    @Test
    public void test222(){
        Scanner in = new Scanner(System.in );
        System.out.print("请输入数的颗树：");
        int trees = Integer.parseInt(in.nextLine().trim());
        peaches = new int[trees];
        for (int i = 0; i < peaches.length; i++) {
            peaches[i] = Integer.parseInt(in.nextLine().trim());
        }
        System.out.println(pick(peaches));
        System.out.println(findMax2(peaches));

    }

/*  5
    2
    3
    156
    15
    6156
    156
    165
    15
    6*/
    // 思路：求出以位置所有 以 peach[i](存入result[i]中)结尾的最长递增子序列的长度--->根据每个 result[0~j],
    // 拿peach[i]和peach[j]比较，如果peach[i]>peach[j]，且result[j]+1>result[i]，很明显，就该把result[i]值加1
    // 所以，这种方法起码能找出一个最长序列，有时候可以找出多条，但有个条件，结尾的peach[i] 一定不相同
    int pick(int[] peaches) {
        int max = 1;
        int length = peaches.length;
        List<ArrayList<Integer>> sequences = new ArrayList<ArrayList<Integer>>();
        
        // 记录每个位置的最长递增子序列的长度
        int result[] = new int[length];
        for (int i = 0; i < length; i++) {
            result[i] = 1;
            ArrayList list= new ArrayList<Integer>();
            list.add(peaches[i]);
            for (int j = 0; j < i; j++) {
                //必須新new一個，不然下面的循环都会操作同一个对象
                ArrayList newL = new ArrayList();
                newL.add(peaches[i]);
                // 如果是i位置大于j位置，且j位置的最长递增子序列的长度+1长于目前i位置的最长递增子序列的长度，则更新i位置的最长递增子序列
                if (peaches[j] <= peaches[i] && result[j] + 1 > result[i]){
                    result[i] = result[j] + 1;
                    newL.addAll(sequences.get(j));
                    list = newL;
                }
            }
            sequences.add(list);
        }
        for (int i : result)
            max = i > max ? i : max;
       /*     
        for(ArrayList<Integer> l : sequences){
            if(l.size() >= max){
                System.out.println(l);
            }
        }   
         */
        return max;
    }
    // 方法二
    private int findMax2(int [] peaches){
        int [] maxV = new int[peaches.length];
        maxV[1] = peaches[0];
        maxV[0] = -1;
        int [] LIS = new int[peaches.length];
        for(int i=0 ; i<LIS.length ; i++){
            LIS[i] = 1;
        }
        int nMaxLIS = 1;
        for(int i=1 ; i<peaches.length ; i++){
            int j;
            for(j = nMaxLIS ; j>=0 ; j--){
                if(peaches[i] >maxV[j]){
                    LIS[i] = j+1;
                    break;
                }
            }
            if(LIS[i] > nMaxLIS){
                nMaxLIS = LIS[i];
                maxV[LIS[i]] = peaches[i];
            }else if( maxV[j]<peaches[i] 
                    &&peaches[i]<maxV[j+1] ){
                maxV[LIS[i]] = peaches[i];
            }
        }
        
        return nMaxLIS;
    }

　　以上多了我自己添加了打印序列的代码，同学们也可以自己屏蔽掉（想看的话，是从后往前看哦，我懒得改了）。同时我也偷了个懒，顺便把第二种发放贴了上去了。在这里继续介绍下去...

　　第二种方法的思路很简单，即开辟一段新的空间存储相应长度LCR中的最大元素的最小元素，举个例子：1，2，5，4 ...  当扫描到5(i=2)的时候，maxV[3] = 5 , LIS[2] = 3 ,maxV[3] 即指的是 长度为3的LCR中最大元素的最小元素，所以当扫描到3的时候，maxV[3]就更新为4了 ， 因为 5>4 ，且他们的LIS的长度都为3

　　这样子，就可以直接比较当前的peach[i]和nMaxLIS就可以算出当前i的LIS

　　这样做是有原因的！ 其实现在这么做的话，效率还是n2 ， 其实还有第三种代码，因为maxV中的记录肯定是满足maxV[1] < maxV[2] <maxV[3] ....细心的同学可以已经发现，这种规律可以用二分查找方法取代遍历 这样就可以把效率提高到 nlog2n （二分查找的效率是log2n）。依据单调递增，将上面便利部分，做以下改动

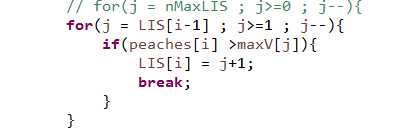
　　最后将上面的代码换成二分查找去匹配，效率应该会更有改善，有兴趣的同学可以尝试

　　以前纯属个人观点，如有错误还请大佬们海涵，还请大佬们指点