在数学中一个非凸的最优化问题是什么意思?
Posted hjlweilong
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了在数学中一个非凸的最优化问题是什么意思?相关的知识,希望对你有一定的参考价值。
作者:王业磊
链接:https://www.zhihu.com/question/20343349/answer/17347657
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
链接:https://www.zhihu.com/question/20343349/answer/17347657
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
数学中最优化问题的一般表述是求取 ,使
,使 ,其中
,其中 是n维向量,
是n维向量, 是
是 的可行域,
的可行域, 是
是 上的实值函数。
上的实值函数。
凸优化问题是指 是闭合的凸集且
是闭合的凸集且 是
是 上的凸函数的最优化问题,这两个条件任一不满足则该问题即为非凸的最优化问题。
上的凸函数的最优化问题,这两个条件任一不满足则该问题即为非凸的最优化问题。
其中, 是 凸集是指对集合中的任意两点
是 凸集是指对集合中的任意两点 ,有
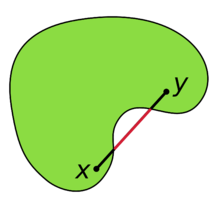
,有 ,即任意两点的连线段都在集合内,直观上就是集合不会像下图那样有“凹下去”的部分。至于闭合的凸集,则涉及到闭集的定义,而闭集的定义又基于开集,比较抽象,不赘述,这里可以简单地认为闭合的凸集是指包含有所有边界点的凸集。
,即任意两点的连线段都在集合内,直观上就是集合不会像下图那样有“凹下去”的部分。至于闭合的凸集,则涉及到闭集的定义,而闭集的定义又基于开集,比较抽象,不赘述,这里可以简单地认为闭合的凸集是指包含有所有边界点的凸集。
 是凸函数是指对于定义域
是凸函数是指对于定义域 中任意两点
中任意两点 ,有
,有 ,直观上就是
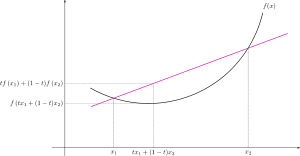
,直观上就是 向下凸出,如下图示意。
向下凸出,如下图示意。
实际建模中判断一个最优化问题是不是凸优化问题一般看以下几点:
凸优化问题是指
其中,


实际建模中判断一个最优化问题是不是凸优化问题一般看以下几点:
- 目标函数
如果不是凸函数,则不是凸优化问题
- 决策变量
中包含离散变量(0-1变量或整数变量),则不是凸优化问题
- 约束条件写成
时,
如果不是凸函数,则不是凸优化问题
以上是关于在数学中一个非凸的最优化问题是什么意思?的主要内容,如果未能解决你的问题,请参考以下文章