51nod1766 树上的最远点对

Posted 2020-10-10 Blue233333

n<=1e5个点的树有边权，m个询问，每次问max dis(i,j) a<=i<=b,c<=j<=d。

结论：一个区间的最远点对，要么是其左半区间的最远点对，要么是其右半区间的最远点对，要么是左右半区间最远点对的四个点的互相组合之一。如下图：

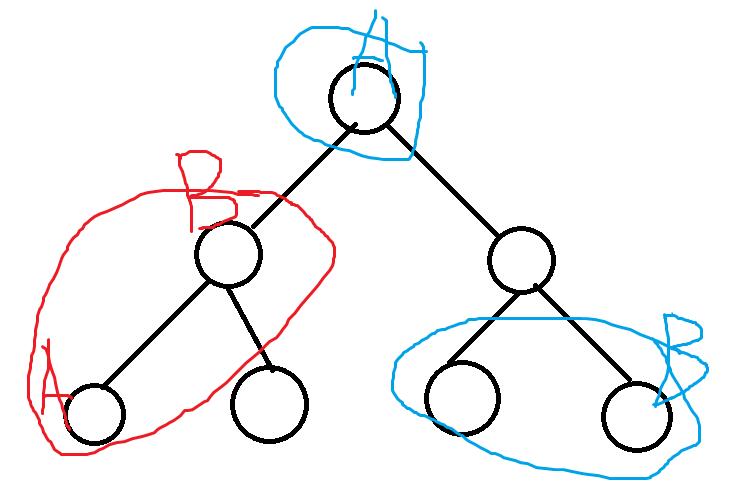
两个集合最远点对分别是A-B，A并B的最远点对是红A-蓝B。

简单证明：一个点到一个点集的最长路径一定是该点到   该点集最远点对这对点的某一点  这样的一条路径。

 

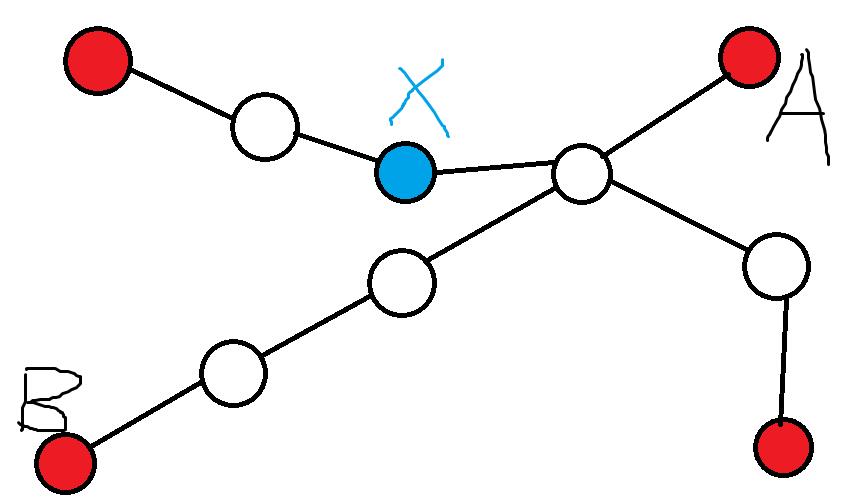
比如红点这个集合，从蓝色点到红色点集的最长路。如果X到达A到B这条链遇到的第一个点是A，那么最远就是X到B；如果X到达A到B这条链遇到的第一个点是B，那么最远就是X到A。如果是像上图这种情况，那么最远点对就是X走到B或X走到A。上图的情况中，设X到左上方点距离a，x到AB链遇到的第一个点C距离b，A到C距离c，B到C距离d，C到右下方的点距离e。可以通过不等式简单加减证明。

所以就用个线段树维护即可，最后把查到两个区间做合并。注意最后一次合并和线段树的合并不一样！！最后的查询问的是两个区间里的点配对，不能把两个点选在同个区间！！

这题时限比较紧，建议不用倍增求lca，这里用了欧拉序加rmq。

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<algorithm>
  4 #include<cstdlib>
  5 #include<cmath>
  6 //#include<iostream>
  7 using namespace std;
  8 
  9 struct Mes
 10 {
 11     int s,t,v;
 12 };
 13 int n;
 14 #define maxn 100011
 15 struct Edge{int to,next,v;}edge[maxn<<1];int first[maxn],le=2;
 16 void in(int x,int y,int v) {Edge &e=edge[le];e.to=y;e.v=v;e.next=first[x];first[x]=le++;}
 17 void insert(int x,int y,int v) {in(x,y,v);in(y,x,v);}
 18 int dep[maxn],pos[maxn]; int ll=0,Log[maxn<<1],rmq[maxn<<1][22];
 19 void dfs(int x,int f)
 20 {
 21 //    cout<<x<<endl;
 22     rmq[++ll][0]=x;pos[x]=ll;
 23     for (int i=first[x];i;i=edge[i].next)
 24     {
 25         const Edge &e=edge[i];if (e.to==f) continue;
 26         dep[e.to]=dep[x]+e.v;
 27         dfs(e.to,x);
 28         rmq[++ll][0]=x;
 29     }
 30 }
 31 void pre()
 32 {
 33     dep[0]=dep[1]=0;dfs(1,0);
 34     Log[0]=-1;for (int i=1;i<=ll;i++) Log[i]=Log[i>>1]+1;
 35     for (int j=1;j<=20;j++)
 36         for (int i=1,to=ll-(1<<j)+1;i<=to;i++)
 37             if (dep[rmq[i][j-1]]<dep[rmq[i+(1<<(j-1))][j-1]])
 38                 rmq[i][j]=rmq[i][j-1];
 39             else rmq[i][j]=rmq[i+(1<<(j-1))][j-1];
 40 }
 41 int lca(int x,int y)
 42 {
 43     x=pos[x],y=pos[y];if (x>y) {int t=x;x=y;y=t;}
 44     int l=Log[y-x+1];
 45     return dep[rmq[x][l]]<dep[rmq[y-(1<<l)+1][l]]?rmq[x][l]:rmq[y-(1<<l)+1][l];
 46 }
 47 int dis(int x,int y)
 48 {
 49     int l=lca(x,y);
 50     return dep[x]+dep[y]-2*dep[l];
 51 }
 52 Mes combine(Mes a,Mes b,bool flag)
 53 {
 54     Mes c;c.v=-1;int tmp;
 55     if ((tmp=dis(a.s,b.s))>c.v)
 56     {
 57         c.v=tmp;c.s=a.s;c.t=b.s;
 58     }
 59     if ((tmp=dis(a.s,b.t))>c.v)
 60     {
 61         c.v=tmp;c.s=a.s;c.t=b.t;
 62     }
 63     if ((tmp=dis(a.t,b.s))>c.v)
 64     {
 65         c.v=tmp;c.s=a.t;c.t=b.s;
 66     }
 67     if ((tmp=dis(a.t,b.t))>c.v)
 68     {
 69         c.v=tmp;c.s=a.t;c.t=b.t;
 70     }
 71     if (flag)
 72     {
 73         if (a.v>b.v && a.v>c.v) c=a;
 74         else if (b.v>a.v && b.v>c.v) c=b;
 75     }
 76     return c;
 77 }
 78 struct SMT
 79 {
 80     struct Node
 81     {
 82         Mes m;
 83         int l,r;
 84         int ls,rs;
 85     }a[maxn<<1];
 86     int size;
 87     SMT() {size=0;}
 88     void up(int x)
 89     {
 90         const int &p=a[x].ls,&q=a[x].rs;
 91         a[x].m=combine(a[p].m,a[q].m,1);
 92     }
 93     void build(int &x,int L,int R)
 94     {
 95         x=++size;
 96         a[x].l=L;a[x].r=R;
 97         if (L==R)
 98         {
 99             a[x].ls=a[x].rs=0;
100             a[x].m.s=L;a[x].m.t=R;
101             a[x].m.v=0;
102             return;
103         }
104         const int mid=(L+R)>>1;
105         build(a[x].ls,L,mid);
106         build(a[x].rs,mid+1,R);
107         up(x);
108 //        cout<<a[x].l<<\'~\'<<a[x].r<<\' \'<<a[x].m.s<<\' \'<<a[x].m.t<<\' \'<<a[x].m.v<<endl;
109     }
110     void build()
111     {
112         int x;
113         build(x,1,n);
114     }
115     int ql,qr;
116     Mes query(int x)
117     {
118         if (ql<=a[x].l && a[x].r<=qr) return a[x].m;
119         else
120         {
121             const int mid=(a[x].l+a[x].r)>>1;
122             bool flag=0;Mes ans;
123             if (ql<=mid) ans=query(a[x].ls),flag=1;
124             if (qr> mid) ans=flag?combine(ans,query(a[x].rs),1):query(a[x].rs);
125             return ans;
126         }
127     }
128     Mes query(int L,int R)
129     {
130         ql=L;qr=R;
131         return query(1);
132     }
133 }t;
134 int m,x,y,v,z;
135 int main()
136 {
137     scanf("%d",&n);
138     for (int i=1;i<n;i++)
139     {
140         scanf("%d%d%d",&x,&y,&v);
141         insert(x,y,v);
142     }
143 //    cout<<":)";
144     pre();
145 //    cout<<":)";
146     t.build();
147 //    cout<<":)";
148     scanf("%d",&m);
149 //    cout<<m<<endl;
150     while (m--)
151     {
152         scanf("%d%d%d%d",&x,&y,&v,&z);
153         Mes ans=combine(t.query(x,y),t.query(v,z),0);
154         printf("%d\\n",ans.v);
155     }
156     return 0;
157 }

View Code