计蒜客 2017 NOIP 提高组模拟赛Day1 T1 小X的质数 线性筛素数

Posted 2020-10-10

小 X 是一位热爱数学的男孩子，在茫茫的数字中，他对质数更有一种独特的情感。小 X 认为，质数是一切自然数起源的地方。

在小 X 的认知里，质数是除了本身和 1 以外，没有其他因数的数字。

但由于小 X 对质数的热爱超乎寻常，所以小 X 同样喜欢那些虽然不是质数，但却是由两个质数相乘得来的数。

于是，我们定义，一个数是小 X 喜欢的数，当且仅当其是一个质数，或是两个质数的乘积。

而现在，小 X 想要知道，在 L到 R 之间，有多少数是他喜欢的数呢？

输入格式

第一行输入一个正整数 Q，表示询问的组数。

接下来 Q 行。包含两个正整数 L 和 R。保证L≤R。

输出格式

输出 Q 行，每行一个整数，表示小 X 喜欢的数的个数。

 

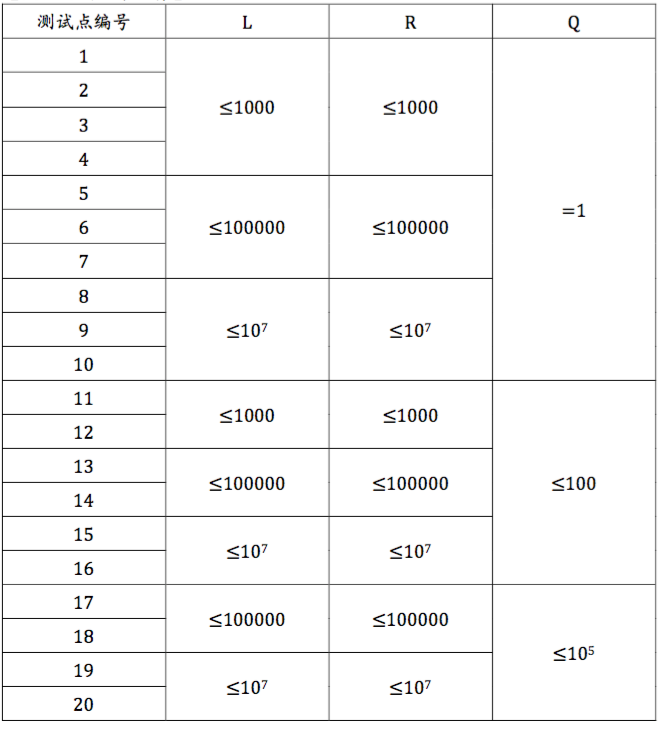
思路：

首先，这题看Q的范围10的5次方，那么肯定会有预处理的操作，也就是说我们需要把每个数之前有多少满足条件的数给统计出来，这里用到了前缀和思想。

接下来是需要求有多少个满足条件的数，那么按照这个数据范围，这个复杂度必须是O(N)级别的，想一想有什么算法能够在线性时间内把一个范围内的素数筛出来呢？

还真的有，那就是欧拉筛，一个优秀的筛法，比埃氏筛的复杂度还优秀。

欧拉筛的原理是每个合数肯定能被它最小的质因数筛去，所以保证了每个数只会被筛一次。

代码：

 1 #include <stdio.h>
 2 
 3 const int maxn = 1e8;
 4 bool not_prime[maxn+5];
 5 int prime[maxn];
 6 int main()
 7 {
 8     int cnt = 0;
 9 
10     for (int i = 2;i <= maxn;i++)
11     {
12         if (!not_prime[i])
13         {
14             prime[cnt++] = i;
15         }
16 
17         for (int j = 0;j < cnt;j++)
18         {
19             if (i * prime[j] > maxn) break;
20 
21             not_prime[i*prime[j]] = 1;
22 
23             if (i % prime[j] == 0) break;
24         }
25     }
26 
27     return 0;
28 }

比较关键的地方是if (i % prime[j] == 0) break;这个语句。这个语句保证了每个合数只会被筛一次。当i % prime[j] = 0时，那么i = k * prime[j]，那么i * prime[j+1] % prime[j] = 0，于是i * prime[j+1]这个数其实已经被prime[j]筛掉了，没有必要继续筛，后面的同理。

那么这道题呢，我们还需要知道质数乘以质数的数量，就在一边筛选的时候一边标记，假设当前的这个数是素数，那么把这个数与素数表中的所有数相乘也是满足条件的数，于是再用一个数组来标记就可以了。

之后我们再用前缀和的思想求一个数之前满足条件的数有哪些，这样就能够在询问的时候O(1)地回答。

代码：

 1 #include <stdio.h>
 2 #include <string.h>
 3 
 4 bool is[10000005];
 5 bool notp[10000005];
 6 
 7 int prime[1000005];
 8 int num[10000005];
 9 
10 int main()
11 {
12     int cnt = 0;
13 
14     for (int i = 2;i <= 10000000;i++)
15     {
16         if (!notp[i])
17         {
18             is[i] = 1;
19 
20             prime[++cnt] = i;
21 
22             for (int j = 1;j <=cnt;j++)
23             {
24                 if (prime[j] * i > 10000000)break;
25 
26                 notp[i*prime[j]] = 1;
27 
28                 is[i*prime[j]] = 1;
29             }
30         }
31         else
32         {
33             for (int j = 1;j <=cnt;j++)
34             {
35                 if (prime[j] * i > 10000000)break;
36 
37                 notp[i*prime[j]] = 1;
38 
39                 if (i % prime[j] == 0) break;
40             }
41         }
42     }
43 
44     for (int i = 1;i <= 10000000;i++)
45     {
46         if (is[i]) num[i] = num[i-1] + 1;
47         else num[i] = num[i-1];
48     }
49 
50     int q;
51 
52     scanf("%d",&q);
53 
54     for (int i = 0;i < q;i++)
55     {
56         int x,y;
57 
58         scanf("%d%d",&x,&y);
59 
60         printf("%d\n",num[y] - num[x-1]);
61     }
62 
63     return 0;
64 }