[51nod] 1766 树上的最远点对
Posted Lev今天学习了吗
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[51nod] 1766 树上的最远点对相关的知识,希望对你有一定的参考价值。
n个点被n-1条边连接成了一颗树,给出a~b和c~d两个区间,表示点的标号请你求出两个区间内各选一点之间的最大距离,即你需要求出max{dis(i,j) |a<=i<=b,c<=j<=d}
(PS 建议使用读入优化)
Input
第一行一个数字 n n<=100000。
第二行到第n行每行三个数字描述路的情况, x,y,z (1<=x,y<=n,1<=z<=10000)表示x和y之间有一条长度为z的路。
第n+1行一个数字m,表示询问次数 m<=100000。
接下来m行,每行四个数a,b,c,d。
Output
共m行,表示每次询问的最远距离
Input示例
5
1 2 1
2 3 2
1 4 3
4 5 4
1
2 3 4 5
Output示例
10
Analysis
洛谷秋令营讲解过的题目,因此并没有用很多时间进行深刻的思考
基本构架:线段树,用于处理区间询问
首先我们有A B两个点集,从A B中各取一个点以组成最远点对,求出其距离
首先可以有这一个结论:最后的最远点对的点,在A中的,必然也是A中最远点对的其中一个点
因此线段树维护每个区间的最远点对,当区间合并的时候取他们各自的最远点对暴力取优即可
(百度一发题解,有人指出最远点对的合并与树的直径的合并具有相似性,因此得出上面的结论)
(但是本蒟蒻很迷啊)
好,接下来谈实现
1. 线段树!
首先线段树基本框架没有问题,我们需要实现一个函数:合并(merge)
这里推荐在单点区间内把最远点对的两个点都设成自己(第一个坑)
不然合并的时候爆炸(我将不存在的点设成了-1结果qwq)
最后的答案要求从A B各取一个点,所以合并函数还需要注意:线段树内的合并可以从单个集合中取点对,而最终答案不行
2. 求距离!
要求求出最近公共祖先(然后瞎搞)
倍增LCA,TLE最后6个点
虽然我没怎么卡常数而且写的非常粗糙(比如没有记忆化每次都要重新求)
但是显然这是算法问题
所以找CCZ求得了一个O(1)LCA的方案
orz ccz!
首先求出当前树的欧拉序(不同于DFS序的是,这里的欧拉序要求包括每一次进入的结点)
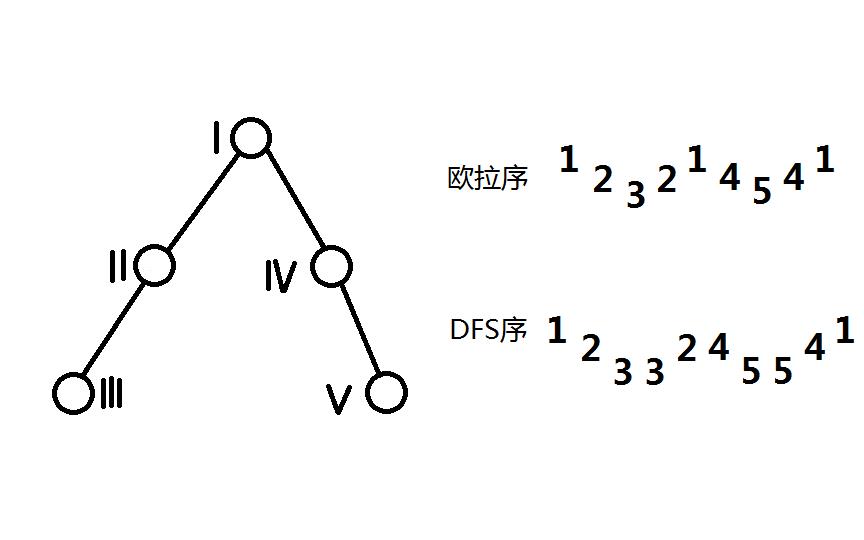
然后对于这份DFS序,我们要做的就是:求出区间(以U V的随便哪个DFN值做区间端点)的最小值(这里的区间保存的是深度Depth)所对应的那个点
显然,那个点就是U V的LCA
而使用ST表的话可以做到O(1)查询
qwq 然而我没学ST表啊 qwq
所以最后跑去看了qt666的博客
qwq (其实代码中的ST表代码是无缝移植qt666的,表示感谢!)
(找个时间还是要重写一遍的,一是不大好无缝移植,趁早学会重造比较好,二是各种调试代码太多)
(敲这道题的时候我居然没有重写)
Code

1 #include<stdio.h> 2 #include<iostream> 3 #define maxn 1000000 4 #define lc (rt<<1) 5 #define rc (rt<<1|1) 6 #define mid ((L+R)/2) 7 using namespace std; 8 9 int dfn[maxn],dfnn[maxn],TIM,line[maxn],chain[maxn],sum[maxn]; 10 int pre[maxn],pre2[maxn],ST[maxn][30]; 11 int fa[maxn][20],ro[maxn][20],depth[maxn],n,m; 12 13 struct edge{ int from,u,v,len; }e[maxn]; 14 int tot,first[maxn]; 15 void insert(int u,int v,int len){ tot++; e[tot].from = first[u], e[tot].u = u , e[tot].v = v , e[tot].len = len, first[u] = tot; } 16 17 void dfs(int now){ 18 dfn[now] = ++TIM; 19 line[TIM] = -depth[now]; 20 chain[TIM] = now; 21 for(int i = first[now];i;i = e[i].from){ 22 int v = e[i].v; 23 if(v != fa[now][0]){ 24 sum[v] = sum[now]+e[i].len; 25 depth[v] = depth[now]+1; 26 fa[v][0] = now; 27 // ro[v][0] = e[i].len; 28 dfs(v); 29 line[++TIM] = -depth[now]; 30 chain[TIM] = now; 31 } 32 } 33 } 34 void Init(){ 35 for(int i = 1;i <= 18;i++) 36 for(int j = 1;j <= n;j++) 37 fa[j][i] = fa[fa[j][i-1]][i-1], 38 ro[j][i] = ro[fa[j][i-1]][i-1]+ro[j][i-1]; 39 } 40 41 void makeST() 42 { 43 pre[0]=1;for(int i=1;i<=20;i++) pre[i]=pre[i-1]<<1; 44 pre2[0]=-1;for(int i=1;i<=TIM;i++) pre2[i]=pre2[i>>1]+1; 45 for(int i=1;i<=TIM;i++) ST[i][0]=i; 46 for(int j=1;j<=20;j++) 47 for(int i=1;i<=TIM;i++){ 48 if(i+pre[j]-1<=TIM){ 49 int x1=ST[i][j-1],x2=ST[i+pre[j-1]][j-1]; 50 if(line[x1]>line[x2]) ST[i][j]=x1; 51 else ST[i][j]=x2; 52 } 53 } 54 }int queryST(int l,int r) 55 { 56 l = dfn[l],r = dfn[r]; 57 if(l > r) swap(l,r); 58 // printf("query:[%d , %d]\\n",l,r); 59 if(l==r)return chain[l]; 60 int x=pre2[r-l+1]; 61 int x1=ST[l][x],x2=ST[r-pre[x]+1][x]; 62 return line[x1]>line[x2]?chain[x1]:chain[x2]; 63 } 64 65 int getdis(int u,int v){ 66 if(depth[u] < depth[v]) swap(u,v); 67 int anc = queryST(u,v); 68 if(anc == v) return sum[u]-sum[anc]; 69 else return sum[u]+sum[v]-sum[anc]*2; 70 /*int ret = 0; 71 if(depth[u] < depth[v]) swap(u,v); 72 for(int i = 18;i >= 0;i--) 73 if(depth[fa[u][i]] >= depth[v]) 74 ret += ro[u][i], 75 u = fa[u][i]; 76 if(u == v) return ret; 77 for(int i = 18;i >= 0;i--) 78 if(fa[u][i] != fa[v][i]) 79 ret += ro[u][i]+ro[v][i], 80 u = fa[u][i],v = fa[v][i]; 81 return ret + ro[u][0] + ro[v][0];*/ 82 } 83 struct node{ int A,B; node(){A = B = -1;}}Tree[maxn*4]; 84 node merge(node a,node b,int mode){ 85 node tmp; 86 // printf("What I get: a.A%d a.B%d b.A%d b.B%d\\n",a.A,a.B,b.A,b.B); 87 int dis = -1; 88 if(a.A > 0 && a.B > 0 && mode){ 89 int cnt = getdis(a.A,a.B); 90 if(cnt > dis) dis = cnt,tmp.A = a.A,tmp.B = a.B; 91 }if(a.A > 0 && b.A > 0){ 92 int cnt = getdis(a.A,b.A); 93 if(cnt > dis) dis = cnt,tmp.A = a.A,tmp.B = b.A; 94 }if(a.A > 0 && b.B > 0){ 95 int cnt = getdis(a.A,b.B); 96 if(cnt > dis) dis = cnt,tmp.A = a.A,tmp.B = b.B; 97 }if(a.B > 0 && b.A > 0){ 98 int cnt = getdis(a.B,b.A); 99 if(cnt > dis) dis = cnt,tmp.A = a.B,tmp.B = b.A; 100 }if(a.B > 0 && b.B > 0){ 101 int cnt = getdis(a.B,b.B); 102 if(cnt > dis) dis = cnt,tmp.A = a.B,tmp.B = b.B; 103 }if(b.A > 0 && b.B > 0 && mode){ 104 int cnt = getdis(b.A,b.B); 105 if(cnt > dis) dis = cnt,tmp.A = b.A,tmp.B = b.B; 106 // cout << "Who visit me qwq?" << endl; 107 } 108 // cout << "dis: " << dis << endl; 109 110 return tmp; 111 } 112 113 void build(int rt,int L,int R){ 114 if(L == R) Tree[rt].A = L,Tree[rt].B = L; 115 else{ 116 build(lc,L,mid); 117 build(rc,mid+1,R); 118 119 Tree[rt] = merge(Tree[lc],Tree[rc],1); 120 } 121 // printf("#%d: L%d R%d A%d B%d\\n",rt,L,R,Tree[rt].A,Tree[rt].B); 122 } 123 124 node query(int rt,int L,int R,int qL,int qR){ 125 if(qL <= L && R <= qR) return Tree[rt]; 126 else{ 127 node tmp; 128 if(qL <= mid) tmp = merge(tmp,query(lc,L,mid,qL,qR),1); 129 if(qR > mid) tmp = merge(tmp,query(rc,mid+1,R,qL,qR),1); 130 // printf("tmp now is: %d %d\\n",tmp.A,tmp.B); 131 return tmp; 132 } 133 } 134 135 int read(){ 136 int ret = 0; char ctr = getchar(); 137 while(ctr < \'0\' || ctr > \'9\') ctr = getchar(); 138 while(ctr >= \'0\' && ctr <= \'9\') ret = ret*10+ctr-\'0\',ctr = getchar(); 139 return ret; 140 } 141 142 int main(){ 143 // scanf("%d",&n); 144 n = read(); 145 for(int i = 1;i < n;i++){ 146 int x,y,z; //scanf("%d%d%d",&x,&y,&z); 147 x = read(),y = read(),z = read(); 148 insert(x,y,z); insert(y,x,z); 149 }depth[1] = 1; dfs(1); Init(); 150 makeST(); 151 // printf("dis(1,3) %d\\n",getdis(1,3)); 152 // scanf("%d",&m); 153 m = read(); 154 // for(int i = 0;i <= TIM;i++){ 155 // for(int j = 0;j <= 9;j++) 156 //// printf("%d ",ST[i][j]); 157 // cout << endl; 158 // } 159 // for(int i = 0;i <= TIM;i++) printf("%d ",line[i]); cout << endl; 160 // for(int i = 0;i <= TIM;i++) printf("%d ",chain[i]); 161 // printf("LCA %d dis(3,4) = %d sum3 %d sum4 %d\\n",queryST(3,4),getdis(3,4),sum[3],sum[4]); 162 // printf("LCA of :%d %d = %d\\n",1,4,query(1,4)); 163 build(1,1,n); 164 while(m--){ 165 int a,b,c,d; 166 // scanf("%d%d%d%d",&a,&b,&c,&d); 167 a = read(),b = read(),c = read(),d = read(); 168 // cout << "AAA"; 169 node ans = merge(query(1,1,n,a,b),query(1,1,n,c,d),0); 170 // cout << "AAA"; 171 // cout << "Great" << ans.A << ans.B << endl; 172 printf("%d\\n",getdis(ans.A,ans.B)); 173 } 174 175 // for(int i = 0;i <= 20;i++) 176 // printf("#%d: %d %d\\n",i,Tree[i].A,Tree[i].B); 177 return 0; 178 }
以上是关于[51nod] 1766 树上的最远点对的主要内容,如果未能解决你的问题,请参考以下文章
