基础算法——图
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基础算法——图相关的知识,希望对你有一定的参考价值。
一、图的概念
图是四类基本逻辑结构集合、线性结构、树形结构和图结构里面的其中一种,即图结构,图结构也是其中最为复杂的结构。在图的结构中,任意两个结点之间都可能相关,即结点之间的邻接关系是任意的。而在树形结构中,结点之间具有层次关系,每一层结点只能和上一层中的至多一个结点相关,但可能和下一层的多个结点相关。图的结构可以描述多种复杂的数据对象,应用较为广泛。
二、各种术语
·有向图、无向图:图G由两个集合V和E组成,记为G=(V,E),其中,v是顶点的有穷非空集合;E是边的集合,边是v中顶点的偶对。若顶点的偶对是有序的则称此图为有向图,有序偶对用尖括号<>括起来;反之,若顶点偶对是无序的,则称此图为无向图,无序偶对用圆括号()括起来。
·权、带权图:图的边附带数值,这个数值叫权。每条边都带权的图称为带权图。
·顶点的度、入度、出度:无向图中顶点v的度是与该顶点相关的边的数目。如果图是一个有向图,则把以顶点v为终点的弧的数目称为v的入度,把以顶点v为始点的弧的数目称为v的出度,入度+出度=有向图的度。
·子图:设G=(V,E)是一个图,若E’是E的子集,V’是V的子集,并且E’中的边仅与V’中的顶点相关联,则图G’=(V’,E’)称为图G的子图。
·路径、路径长途:无向图的路径是一个顶点到另一个顶点所经过的边,所经过的边的数目称为路径长度;有向图的路径是一个顶点到另一个顶点的弧,路径长度是路径上面弧的数目。
·连同、连通图、连通分量:在无向图中,如果从顶点v到顶点v’有路径,则称v和v’是连通的。如果图中的任意两个顶点vi和vj都是连通的,则称此图为连通图。
强连通、强连通图、强连通分量:对于无向图,如果图中任意一对顶点vi和vj(i!=j)都有顶点vi到vj的路径也有vj到v?的路径,即两个顶点双向连通,那么称该有向图为强连通图。有向图的极大强连通子图称为强连通分量。
·生成树、生成森林:一个连通图的生成树,是含有该连通图的全部顶点的一个极小连通子图。若连通图G的顶点个数为n,则G的生成树的边数为n-1。如果G的一个子图G’的边数大于n-1,则G’中一定有环。相反,如果G’的边数小于n-1,则G’一定不连通。在非连通图中,由每个连通分量都可得到一个极小连通子图,即一棵生成树,这些连通分量的生成树组成了一个非连通图的生成森林。
这些概念是在解题时必要的一些储备,需要重点记忆与理解。
三、图的存储
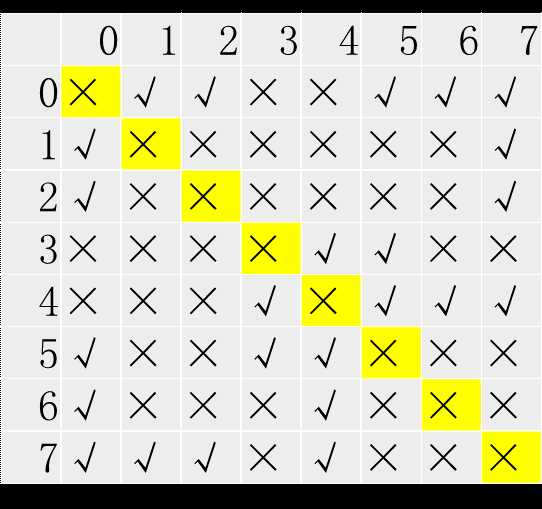
1. 邻接矩阵:图的邻接矩阵(Adjacency Matrix)表示是采用二维数组的方式。通过邻接矩阵可以立刻看出两顶点之间是否存在一条边,只需要检查邻接矩阵重行i和列j是否是非零值。对于无向图,邻接矩阵是对称的。
注:一个图的邻接矩阵是唯一的,但其邻接表表示不唯一。这是因为邻接表表示中,各边表结点火器的链接次序取决于建立邻接表的算法以及边的输入次序。也就是说,在邻接表的每个线性链表中,各结点的顺序是任意的。
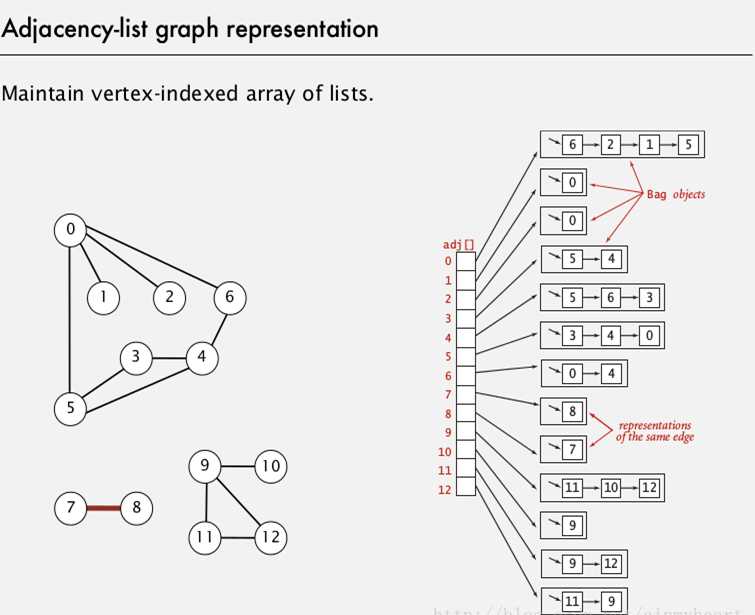
2. 邻接表
练习题:
1.在一个图中,所有顶点的度数之和等于所有边数的 倍。
A. 1/2 B. 1 C. 2 D. 4
2.在一个有向图中,所有顶点的入度之和等于所有顶点的出度这和 倍。
A. 1/2 B. 1 C. 2 D. 4
3.一个有n个顶点的无向图最多有 条边。
A. n B. n(n-1) C. n(n-1)/2 D. 2n
4.具有4个顶点的无向完全图有 条边。
A. 6 B. 12 C. 16 D. 20
5.具有6个顶点的无向图至少应有 条边才能确保是一个连通图。
A. 5 B. 6 C. 7 D. 8
6.在一个具有n个顶点的无向图中,要连通全部顶点至少需要 条边。
A. n B. n+1 C. n-1 D. n/2
7.对于一个具有n个顶点的无向图,若采用邻接矩阵表示,则该矩阵的大小是 。
A. n B. (n-1)2 C. n-1 D. n2
8.对于一个具有n个顶点和e条边的无向图,若采用邻接矩阵表示,则表头向量的大小是 1 ;所有邻接矩阵中的结点总数是 2 。
1 A. n B. n+1 C. n-1 D. n+e
2 A. e/2 B. e C. 2e D. n+e
9.已知一个图如图所示,若从顶点a出发按深度搜索法进行遍历,则可得到顶点序列为 1 ;按宽度搜索法进行遍历,则可得到顶点序列为 2 。
1 A. abecdf B. acfebd C. aebcfd D. aedfcb
2 A. abcedf B. abcefd C. aebcfd D. acfdeb
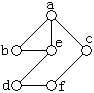
第9题图
10.已知一有向图的邻接表存储结构如图所示
(1)根据有向图的深度优先遍历算法,从v1顶点出发,所得到的顶点序列是 1 。
(2)根据有向图的宽度优先遍历算法,从v1顶点出发,所得到的顶点序列是 2 。
1 A. v1,v2,v3,v5,v4 B. v1,v2,v3,v4,v5
C. v1,v3,v4,v5,v2 D. v1,v4,v3,v5,v2
2 A. v1,v2,v3,v4,v5 B. v1,v3,v2,v4,v5
C. v1,v2,v3,v5,v4 D. v1,v4,v3,v5,v2
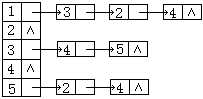
第10题图
11.采用邻接表存储的图的深度优先遍历算法类似于二叉树的 。
A. 先序遍历 B. 中序遍历 C. 后序遍历 D. 按层遍历
12.采用邻接表存储的图的宽度优先遍历算法类似于二叉树的 。
A. 先序遍历 B. 中序遍历 C. 后序遍历 D. 按层遍历
13.判定一个有向图是否存在回路除了可以利用拓扑排序方法外,还可以利用 。
A. 求关键路径方法 B. 求最短路径的Dijkstra方法
C. 宽度优先遍历算法 D. 深度优先遍历算法
填空题
1.n个顶点的连通图至少 条边。
2.在无权图G的邻接矩阵中,若 (vi, vj) 或 <vi, vj> 属于图G的边集,则对应元素A[i][j] 等于 ,否则等于 。
3.在无权图G的邻接矩阵中,若A[i][j]等于1,则等于A[j][i] = 。
4. 已知图G的邻接表如图所示,其从v1顶点出发的深度优先搜索序列为 ,其从v1顶点出发的宽度优先搜索序列为 。
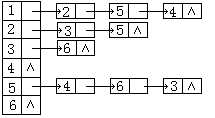
第4题图
5.已知一图的邻接矩阵表示,计算第i个结点的入度的方法是 。
6.已知一图的邻接矩阵表示,删除所有从第i个结点出发的边的方法是 。
以上是关于基础算法——图的主要内容,如果未能解决你的问题,请参考以下文章