朴素贝叶斯分类

Posted 2020-10-09 懵懂的菜鸟

朴素贝叶斯分类

1 朴素贝叶斯分类

监督学习可以从概率的角度来认识，分类的任务可以看做是给定一个测试样例后，估计目标出现的条件概率，即后验概率。

首先给出条件概率公式，即：

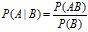
然后给出，贝叶斯定理：

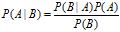
朴素贝叶斯分类是一种十分简单的分类算法，叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素，朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。

朴素贝叶斯分类的正式定义如下：

1，设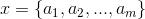为一个待分类项，而每个a为x的一个特征属性。

2，有类别集合。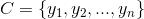

3，计算。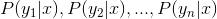

4，如果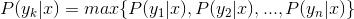，则。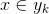

朴素贝叶斯分类分为三个阶段：

（1）准备工作阶段准备工作阶段，输入时待分类数据，输出是特征属性和训练样本；

（2）分类训练阶段，输入是特征属性和训练样本，输出是分类器；

（3）应用阶段，输入是分类器和待分类项，输出是分类项与类别的映射关系。

朴素贝叶斯的思想应用于文本分类时，我们只需要计算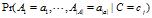即可，我们假设所有属性都是条件独立于类别。即可得到

公式一：

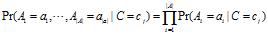
公式二：

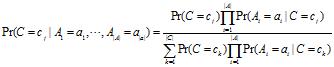
如果仅仅需要总体上最有可能的类别作为所有测试样例做预测，我们只需要公式二的分子即可。所以，我们可以通过下面的公式来对测试样例的类别做预测。

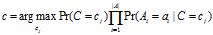
构造朴素贝叶斯分类器所需要的概率值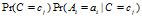可以经过一次扫描得到，所以算法相对训练样本的数量是线性的，这是朴素贝叶斯分类器的优势之一，效率很高。

为了研究实际可用的分类器，需要解决一些特别的问题：如处理的数值属性、丢失的属性值和估计产生的零概率。

数值的离散化：

对连续特征进行离散化处理，一般经过以下步骤：（1）对此特征进行排序。特别是对于大数据集，排序算法的选择要有助于节省时间，提高效率，减少离散化的整个过程的时间开支及复杂度。（2）选择某个点作为候选点，用所选取的具体的离散化方法的尺度来衡量候选选点是否满足要求。（3）若候选点满足离散化的衡量尺度，则对数据集进行分裂或合并，再选择下一个候选点，重复步骤（2）（3）。（4）当离散算法存在停止准则时，如果满足停止准则，则不再进行离散化过程，从而得到最终的离散结果。^[2]

丢失的属性值:

丢失的属性值一般可以忽略。

估计产生的零概率：

在一个测试数据中出现属性值可能不在训练数据中出现，则对应的概率即为0,从而导致分类出现错误。一个主要的解决办法便是加入一个小样本叫校正。

令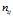为同时满足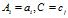的样本数量，令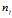为训练数据中的数据总数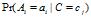，未校正前的估计是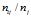，校正后的估计是

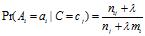
其中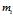为的类型数目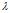，是一个引子，一般为1/n（n是训练数据D的总数）。当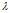=1时，就是著名的Laplace延续率（拉普拉斯延续率）。校正后的公式称为lidstone延续率。

 

参考文献：

[1] http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html

[2] https://wenku.baidu.com/view/264abca16f1aff00bed51ed7.html