傅里叶变换（FFT）的多相滤波结构实现

Posted 2020-10-08

作者：桂。

时间：2017-09-25  14:53:01

链接：http://www.cnblogs.com/xingshansi/p/7591868.html 

---

前言

以前在梳理信号频域变换的时候，提到逆序级联FFT（Inverse cascade FFT）的实现思路，后来分析多相滤波信道化，才发现其实Cascade FFT就是FFT的多相结构实现，在此系统梳理一下。

一、多相结构FFT实现

　　A-传统测频技术分析

信号的短时傅里叶变换（STFT）可表示为：

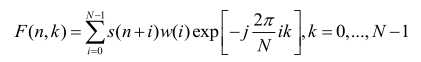
其中s为输入信号，w为对应窗函数。长度为N，k为对应频率（信道），n为对应时刻。

一般的测频思路是：AD采样，加窗，FFT实现，门限检测以及频率检测（粗测频），借助Rife算法实现精确测频。

其中，FFT实现步骤为了进一步节约资源，通常利用MoniFFT的思路，即进一步对频点就行量化。

这里存在一个平滑点数与处理时间的制约关系（对应就是短时傅里叶变换，short-time fourier transform，STFT）：

　　窗函数的滑动步长决定了短时傅里叶变换的时域分辨率，对其运算时间裕度、输出数据量等也造成很大影响。当窗口不交叠的滑动时时域分辨率最差，输出数据率低，留给 FFT 模块的信号处理时间长，滑动距离变小时，时域分辨率提高，数据输出率也增加，留给 FFT 模块的数据处理时间变少。当系统工作在高速率，且要求较高的时频分辨率时，基于短时傅里叶变换的接收机将面临实时处理的瓶颈，并且大量高速的数据输出也会对后续处理环节造成计算量和计算时间上的压力。

　　B-多相测频技术分析

当数据量大，且要求较高时频分辨率时，可以借助多相结构来实现FFT的运算思路。

信号STFT重写为：

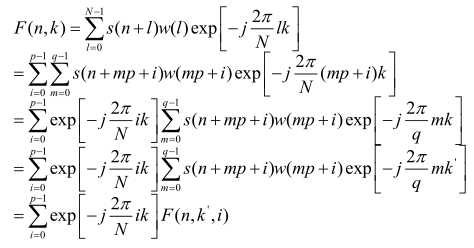
 对应多相FFT实现思路：抽取 - 乘以对应抽取的窗函数 - FFT变换 - 乘法器（补偿因子） -  并行FFT处理 - 并串转换。

 

二、仿真验证

 对应代码实现：

clc;clear all;close all;
%orignal signal
fs = 200;
f0 = 30;
t = 0:1/fs:2;
x = sin(2*pi*f0*t‘);
Na = 2^nextpow2(length(x));
sig = [x;zeros(Na-length(x),1)];
%polyphase FFT
N=16;M=Na/N;
sr = reshape(sig,M,N).‘;
sr = fft(sr);
P = exp(-1j*2*pi*[0:N-1]‘*[0:M-1]/M/N);
sr=sr.*P;
sr = fft(sr.‘).‘;
%save result
X_CaFFT = sr(:);
%plot
xf = linspace(0,fs,Na);
plot(xf,abs(X_CaFFT),‘k‘);grid on;hold on;
xlabel(‘频率（Hz）‘);
ylabel(‘幅度‘);

　　对应仿真结果：

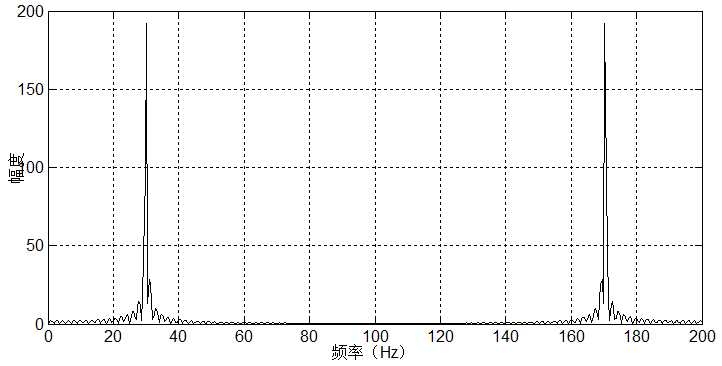
主要实现架构：

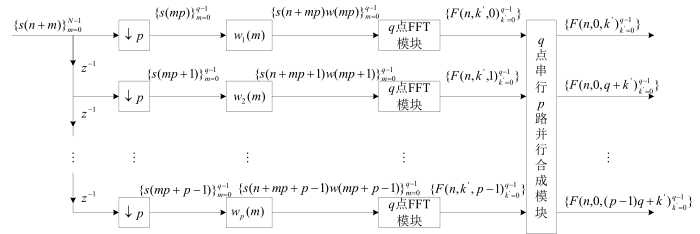
合成模块技术细节：

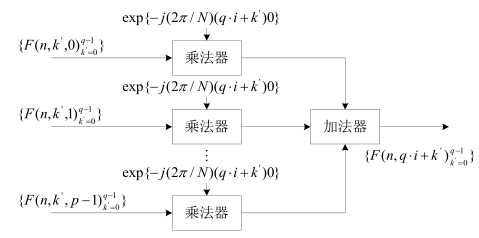
此处的乘法器，对应算法实现，可以是直接的乘法器 / 也可以是乘法器（相位因子相乘）与FFT的级联实现。