傅里叶变换+频域滤波
Posted 乖乖怪123
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了傅里叶变换+频域滤波相关的知识,希望对你有一定的参考价值。
傅里叶变换+频域滤波
cv2.imread()基本参数介绍
Mat cv::imread(const String & filename, int flags = IMREAD_COLOR)
retval = cv.imread(filename[, flags])
# ilename:需要打开图片的路径,可以是绝对路径或者相对路径,路径中不能出现中文
# flag:图像的通道和色彩信息(默认值为1)
# flag = -1, 8位深度,原通道
# flag = 0, 8位深度,1通道
# flag = 1, 8位深度,3通道
# flag = 2, 原深度, 1通道
# flag = 3, 原深度, 3通道
# flag = 4, 8位深度,3通道
傅里叶变换
时域图像,频域图像
正常傅里叶变换后不做任何处理(不经过平移处理)的话应该是四角亮,中间暗
频域图像中亮的为低频信息,暗的为高频信息
自然图像一般都是低频信息多于高频信息
什么是频域
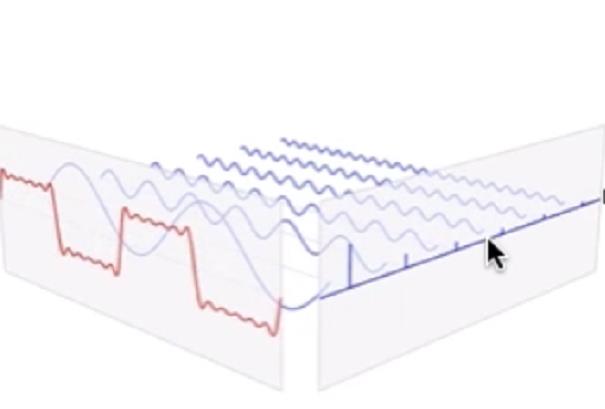
越往里面频率越来越高
振幅关于频域的函数
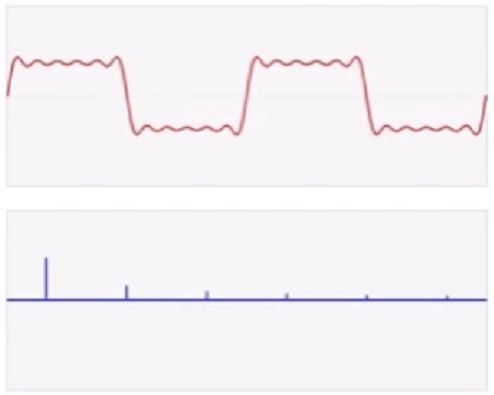
傅里叶变换的由来
傅里叶级数
对于任何以
2
π
2\\pi
2π 为周期的函数,都可以由三角函数来拟合??
f
(
t
)
=
a
0
2
+
∑
n
=
1
+
∞
(
a
n
cos
n
t
+
b
n
sin
n
t
)
f(t)=\\fraca_02+\\sum_n=1^+\\infty\\left(a_n \\cos n t+b_n \\sin n t\\right)
f(t)=2a0+n=1∑+∞(ancosnt+bnsinnt)
三角函数系正交性
∫ − π + π sin k x cos n x d x = 0 ∫ − π + π sin k x sin n x d x = 0 , k ≠ n π , k = n ≠ 0 ∫ − π + π cos k x cos n x d x = 0 , k ≠ n π , k = n ≠ 0 \\beginarrayl \\int_-\\pi^+\\pi \\sin k x \\cos n x d x=0 \\\\ \\int_-\\pi^+\\pi \\sin k x \\sin n x d x=\\left\\\\beginarrayl 0, k \\neq n \\\\ \\pi, k=n \\neq 0 \\endarray\\right. \\\\ \\int_-\\pi^+\\pi \\cos k x \\cos n x d x=\\left\\\\beginarrayl 0, k \\neq n \\\\ \\pi, k=n \\neq 0 \\endarray\\right. \\endarray ∫−π+πsinkxcosnxdx=0∫−π+πsinkxsinnxdx=0,k=nπ,k=n=0∫−π+πcoskxcosnxdx=0,k=nπ,k=n=0
正交性的证明:
1 ) : ∫ − π + π sin k x cos n x d x = 1 2 ∫ − π + π [ sin ( k + n ) x + sin ( k − n ) x ] d x ( 积化和差 ) 当 k ≠ n 时 , 上式 = − 1 2 [ cos ( k + n ) x k + n + cos ( k − n ) x k − n ] − n + n = 0 当 k = n 时 , 上式 = ∫ − π + π sin k x cos n x d x = 1 2 ∫ − π + π sin 2 k x d x = 0 2 ) : ∫ − π + π sin k x sin n x d x = 1 2 ∫ − π + π [ cos ( k − n ) x − cos ( k + n ) x ] d x ( 积化和差 ) 当 k ≠ n 时,上式 = 1 2 [ sin ( k − n ) x k − n − sin ( k + n ) x k + n ] − π + π = 0 当 k = n ≠ 0 时 , 上式 = 1 2 ∫ − π + π ( 1 − cos 2 k x ) d x = π 1): \\int_-\\pi^+\\pi \\sin k x \\cos n x d x=\\frac12 \\int_-\\pi^+\\pi[\\sin (k+n) x+\\sin (k-n) x] d x \\quad (积化和差)\\\\ 当 k \\neq n 时,上式 =-\\frac12\\left[\\frac\\cos (k+n) xk+n+\\frac\\cos (k-n) xk-n\\right]_-n^+n=0 \\\\ 当 k=n 时,上式 =\\int_-\\pi^+\\pi \\sin k x \\cos n x d x=\\frac12 \\int_-\\pi^+\\pi \\sin 2 k x d x=0 \\\\ \\\\ 2): \\int_-\\pi^+\\pi \\sin k x \\sin n x d x=\\frac12 \\int_-\\pi^+\\pi[\\cos (k-n) x-\\cos (k+n) x] d x (积化和差)\\\\ 当 k \\neq n 时,上式 =\\frac12\\left[\\frac\\sin (k-n) xk-n-\\frac\\sin (k+n) xk+n\\right]_-\\pi^+\\pi=0 \\\\ 当 k=n \\neq 0 时,上式 =\\frac12 \\int_-\\pi^+\\pi(1-\\cos 2 k x) d x=\\pi 1):∫−π+πsinkxcosnxdx=21∫−π+π[sin(k+n)x+sin(k−n)x]dx(积化和差)当k=n时,上式=−21[k+ncos(k+n)x+k−ncos(k−n)x]−n+n=0当k=n时,上式=∫−π+πsinkxcosnxdx=21∫−π+πsin2kxdx=02):∫−π+πsinkxsinnxdx=21∫−π+π[cos(k−n)x−cos(k+n)x]dx(积化和差)当k=n时,上式=21[k−nsin(k−n)x−以上是关于傅里叶变换+频域滤波的主要内容,如果未能解决你的问题,请参考以下文章
Opencv 实现图像的离散傅里叶变换(DFT)卷积运算(相关滤波)
