06 Theory of Generalization

Posted 2020-10-07

若H的断点为k，即k个数据点不能被H给shatter，那么k+1个数据点也不能被H给shatter，即k+1也是H的断点。

如果给定的样本数N是大于等于k的，易得mH(N)<2N，且随着N的增大，小得越来越多。

当断点为k时，记最大可能的成长函数mH(N)为bound函数，记为B(N,k)。------只和N、k有关

注意比较，发现bound函数比起成长函数消除了H。

如果无断点，自然没有B(N,k)什么事；

如果断点为k，

那么mH(N)是给定H下，可能的最大假设类数；

B(N,k)是不限H下，可能的最大假设类数。

B(N,k)=maxH mH(N)，只和样本数N和断点k有关。

注意：这里的H要求有相同的k。

通过数学归纳法可证得：B(N,k)实际被Nk-1所框住，既然成长函数的上限被N的多项式给框住，易得，如果断点存在的话，成长函数也是多项式型的。

------证明了上一节的猜想。

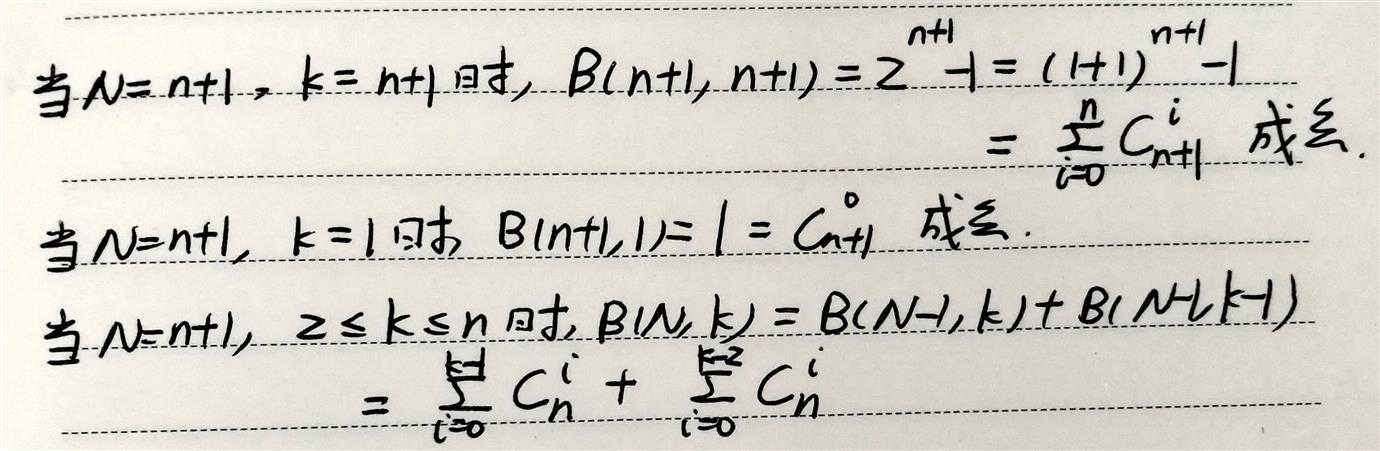
再看保证Ein和Eout的不等式，

证明，

1.用和训练集同样大小的测试集上的表现替代整体输入空间上的表现，认为使得训练集内和整体表现差异过大的坏数据也会使得训练集和测试集上的表现差异过大；

这里做了2件事：

一是用有限的训练集+有限的测试集替代了无限的输入空间，将无限的X变为数量为2N的有限数据集；

二是用完美划分该有限数据集的模式f‘代替了完美划分整个输入空间的模式f。------进行了松弛，因为f‘的数量多于f。

2.用有限类数mH(2N)替代无限|H|；

3.使用不放回的霍夫丁不等式。

对应于在取小球实验里不放回地抽取，取出的橘色小球频率和罐子里剩余的橘色小球概率依旧概率近似相等。------因为 the inequalities also hold when the Xi have been obtained using sampling without replacement; in this case the random variables are not independent anymore.（来自维基百科）

得到VC bound。

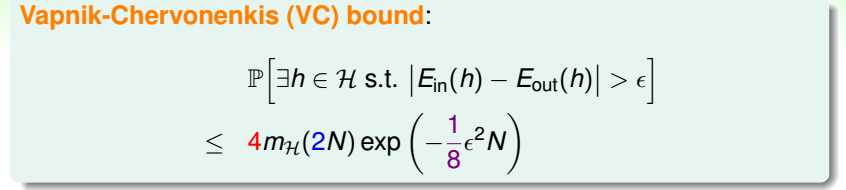
所以，

2维感知器算法在训练集D上学习到的g泛化到整个输入空间X上是概率近似可行的。

那3维及以上感知器算法呢？