CS224W摘要09.Theory of Graph Neural Networks

Posted 2021-10-14 oldmao_2000

文章目录

• How powerful are GNNs?
• • local neighborhood structures
  • Computational graph
  • Injective Function
• Designing the Most Powerful Graph Neural Network
• • injective multiset function
  • GIN vs WL graph Kernel

CS224W: Machine Learning with Graphs
公式输入请参考： 在线Latex公式
这节内容有点散（虚），主要是围绕GNN的表达能力来展开的，思路如下：
1、复习下GNN的原理就是通过邻居的aggregation来进行消息传递，这里引出计算图概念
2、GNN的表达能力主要是指模型区分图是否同构的能力
3、识别同构能力和aggregation选择的函数有关系，函数如果是injection function（B站机翻得好污，还是用原文好了），那么消息传递过程不会丢失信息，否则会有消息丢失
4、理论上，GNN的表达能力的上限是WL test，与其基本等价的是GIN模型
5、可以有别的方式来帮助GNN来突破WL test上限，这里先挖坑
下面就把一些重要知识点列一下。

How powerful are GNNs?

Many GNN models have been proposed (e.g., GCN, GAT, GraphSAGE, design space).
What is the expressive power (ability to distinguish different graph structures) of these GNN models?
指模型区分图是否同构的能力
How to design a maximally expressive GNN model?
使用injection function做聚合函数

local neighborhood structures

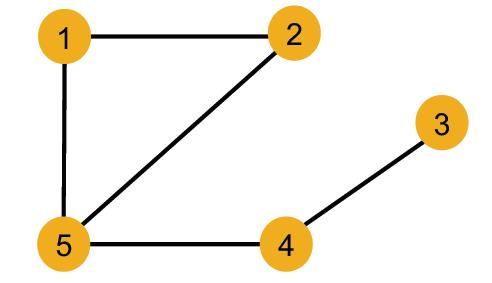
这里给了一个例子，看如何识别不同节点，这里节点虽然id不一样，但是特征是一样的，因为特征用颜色标识。这里看GNN如何在特征相同的情况下识别出不同节点

例子	结果
Nodes 1 and 5	different	度不一样
Nodes 1 and 4	different	度一样，但邻居的度不一样
Nodes 1 and 2	same	度一样，邻居的度也一样

根据上表，思考GNN是否能识别节点1和2？先看GNN的表示方法，计算图。

Computational graph

计算图概念：A GNN generates node embeddings through a computational graph defined by the neighborhood.

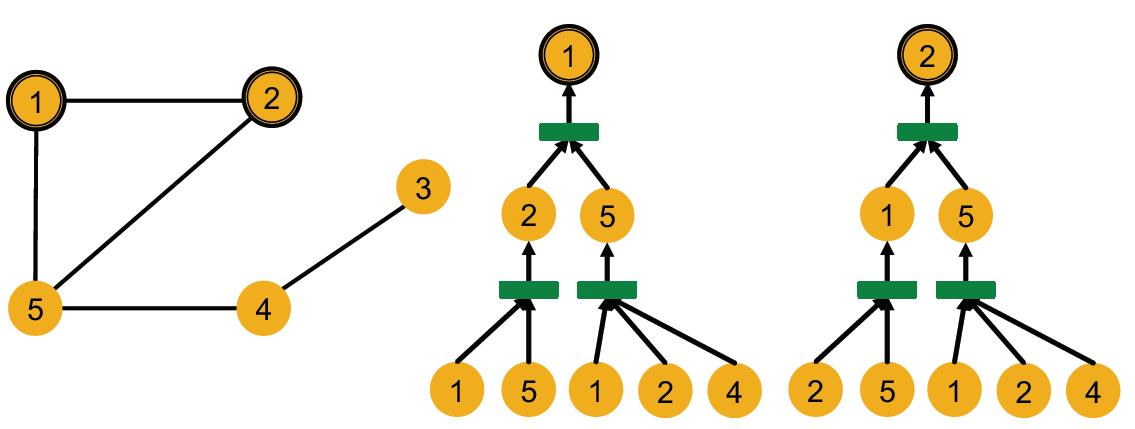
虽然有id不一样，但是特征一样（看颜色），GNN不吃id，只吃特征做输入，因此节点1和2的计算图是一样的，因此aggregation操作得到的embedding也会一样。
完整的计算图是一个rooted subtree structures.

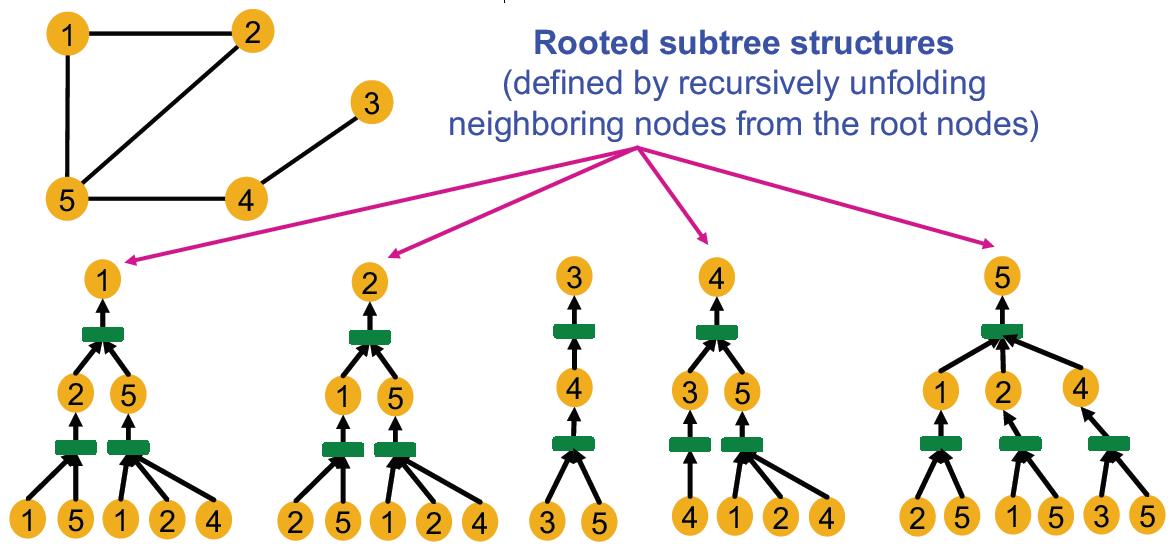
GNN就是将每个rooted subtrees映射到不同embedding（颜色）

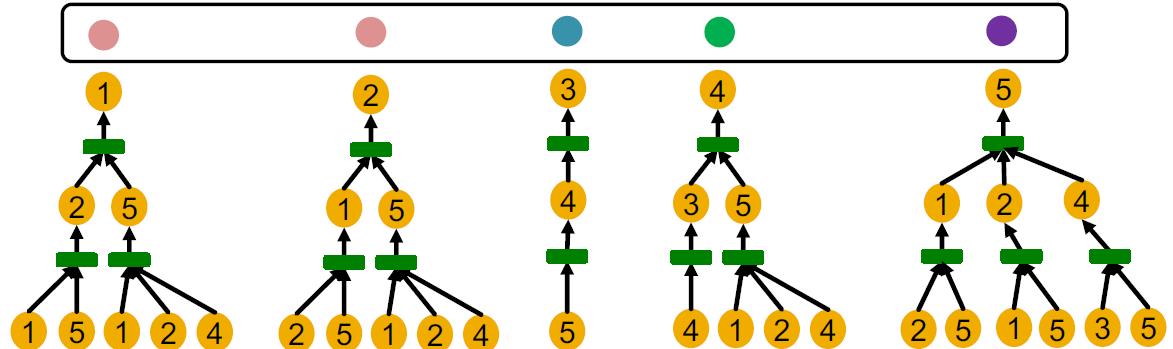
Injective Function

定义：Function 𝑓: 𝑋 → Y is injective if it maps different elements into different outputs.
满足上面的条件的函数可以最大限度的保留输入的信息。

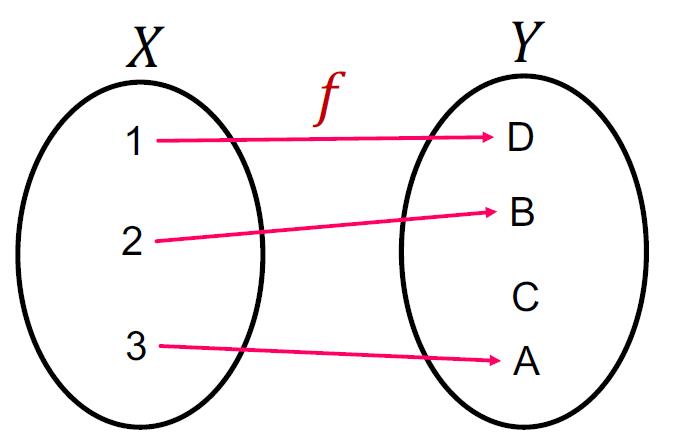
因此可以推出：应该根据计算图作为输入，然后得到injective 的结果，这样的GNN的表达能力最大。要做到这点，那么要保证计算图这个树中每一层孩子向父亲汇聚的的过程都应该是injective 的：

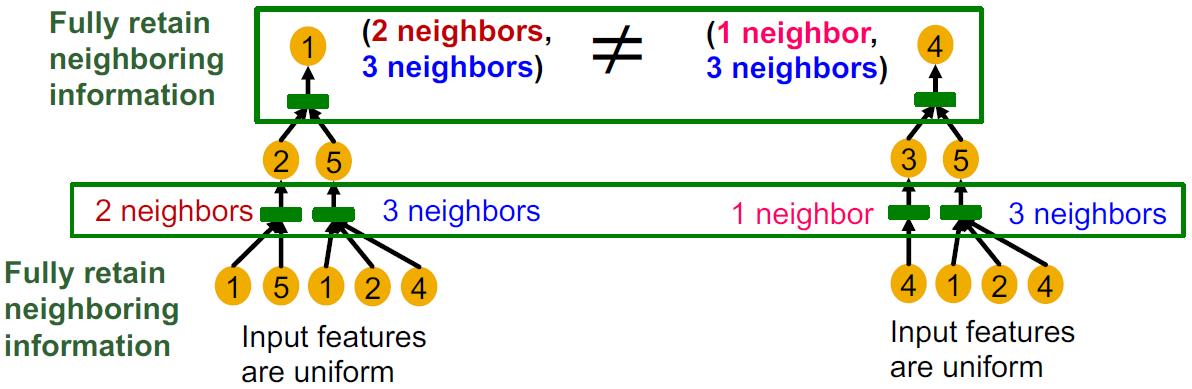
也就是每一层都是：injective neighbor aggregation, Maps different neighbors to different embeddings.

Designing the Most Powerful Graph Neural Network

有了上面的理论，下面看怎么把这个injective neighbor aggregation融入到GNN的设计上。并分析不同aggregation不同的injective（或者说表达能力）能力。
这里的内容其实在GIN里面有讲。。。
multi-set概念：set with repeating elements，例子：

GNN就是将邻居节点（multi-set）进行聚合的过程
Expressive power of GNNs can be characterized by that of the neighbor aggregation function.
Neighbor aggregation is a function over multi-sets (sets with repeating elements)
无论是sum、mean、max的aggregation方式都不是injective函数，因此会有识别情况（具体可以看GIN论文）：

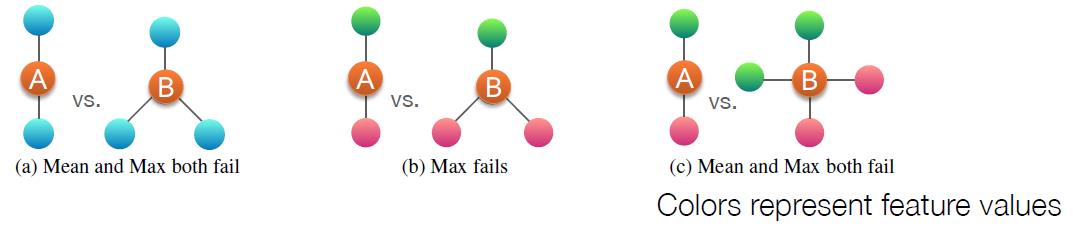
三个函数表达能力如下：

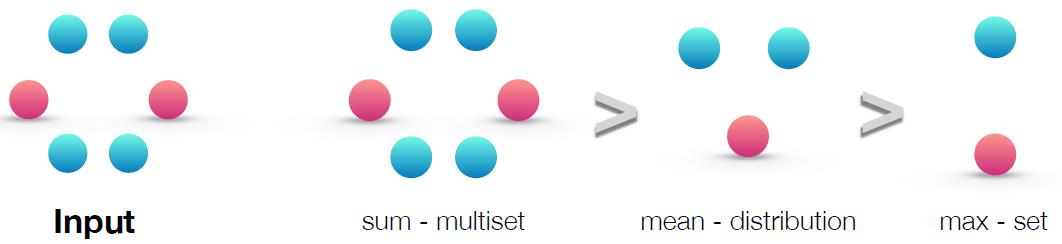
injective multiset function

根据一个定理：Universal Approximation Theorem
1-hidden-layer MLP with sufficiently-large hidden dimensionality and appropriate non-linearity 𝜎(⋅) (including ReLU and sigmoid) can approximate any continuous function to an arbitrary accuracy.

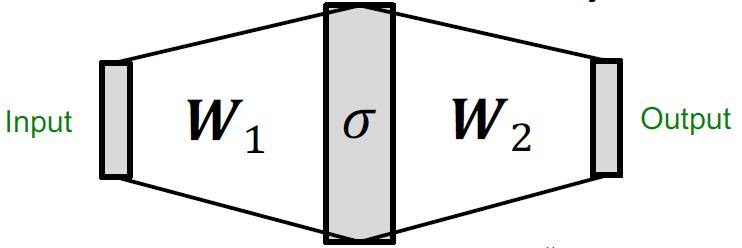
这里用MLP来作为injective multiset function. In practice, MLP hidden dimensionality of 100 to 500 is sufficient.
要达到的效果是：

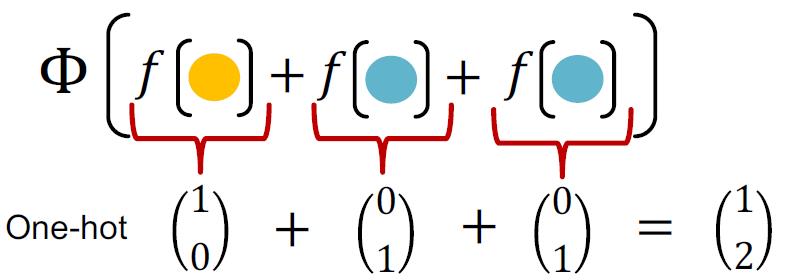
可以明显的计算各个颜色的节点的个数
数学表达是：
$$\Phi \left(\sum _{x\in S}f(x)\right)$$
这里用MLP来搞定上面的两个函数：
$$ML{P}_{\Phi }\left(\sum _{x\in S}ML{P}_f(x)\right)$$
这个表达形式就是GIN模型。GIN is THE most expressive GNN in the class of message-passing GNNs!
下面是证明，GIN模型与WL graph kernel等价。

GIN vs WL graph Kernel

GIN can be understood as differentiable neural version of the WL graph Kernel:

Advantages of GIN over the WL graph kernel are:
§ Node embeddings are low-dimensional; hence, they can capture the fine-grained similarity of different nodes.
§ Parameters of the update function can be learned for the downstream tasks.