算法-最大矩形(动态规划)

Posted 2020-10-07

不说废话了，直接贴题

题意：

给你一个二维矩阵，权值为False和True，找到一个最大的矩形，使得里面的
值全部为True，输出它的面积

样例：

给你一个矩阵如下

[
  [1, 1, 0, 0, 1],
  [0, 1, 0, 0, 1],
  [0, 0, 1, 1, 1],
  [0, 0, 1, 1, 1],
  [0, 0, 0, 0, 1]
]
输出6

1.建立模型

   这个题如果直接来解决的话，可能有很大的难度，所以，我们必须先建立模型。

   首先我们来看一个题，是LeetCode上：

  题意：

Given n non-negative integers representing the histogram‘s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

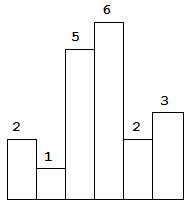
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

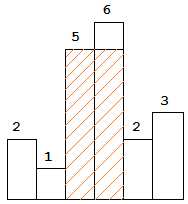
The largest rectangle is shown in the shaded area, which has area = 10 unit.

样例：

For example,
Given heights = [2,1,5,6,2,3],
return 10.

 (1).暴力解法

   这个题暴力解法非常的简单，就是遍历数组，向前和向后计算当前柱状图能够构成的最大矩形。至于解法这里不详述，我们的目的引出另一个方法。

 (2).栈法

   解题思路：首先我们将第一个柱状图在数组里面的下标(之后称为下标)压栈，之后的柱状图需要我们来判断是否需要压栈。如果新的柱状图高度大于栈顶柱状图的高度，那么就当前这个柱状图的下标压栈；如果小于的话，那么我们可以计算当前栈顶及其之前的柱状图面积，于是，我们将栈顶的下标pop出来，计算它的面积。

    pop之后，我们再次判断当前的栈顶的高度是否大于新柱状图的高度，如果大于，则压栈；反之，则计算面积，这里计算面积的时候需要注意的是：计算pop出来的柱状图的面积(从pop出来的柱状图到新的柱状图，不包含新的柱状图，因为新的柱状图的高度小于当前pop出来的高度)高度等于它本身的高度，而宽度则是当前的新的柱状图的下标-pop出来的之后的栈顶的下标 - 1。

  为什么是这样呢？因为pop出来的之后的栈顶柱状图与pop出来的柱状图之间可能还有其他柱状图，只是在之前的操作被pop出去了，所以，这里需要这样计算宽度。

  如果理解了思路，那么代码就非常理解了

 1     public int largestRectangleArea(int[] heights) {
 2         if (heights == null || heights.length == 0) {
 3             return 0;
 4         }
 5         Stack<Integer> stack = new Stack<>();
 6         //压入第一个柱状图的下标
 7         stack.push(0);
 8         int i = 1;
 9         int max = heights[0];
10         //当i < heights.length 或者栈不为空时，这里之所以需要判断栈不为空，是因为
11         //可能有些高度很小的柱状图，一直停留在栈中，没有机会pop出来计算面积，所以最后需要一一的pop出来
12         //计算面积
13         while (i < heights.length || (i == heights.length && !stack.isEmpty())) {
14             //当当前的高度大于大于栈顶的高度或者栈为空时，将当前的下标压栈
15             if (i < heights.length && (stack.isEmpty() || heights[stack.peek()] <= heights[i])) {
16                 stack.push(i);
17                 i++;
18             } else { //计算面积
19                 int top = heights[stack.pop()]; //得到栈顶的高度
20                 //计算面积，当当前的栈为空时，直接是top * i（i里面已经包含了中间被pop出去的柱状图）；不为空时，
21                 //则使用相对位置计算
22                 int currMax = !stack.isEmpty() ? (i - stack.peek() - 1) * top : top * i;
23                 //更新最大值
24                 max = Math.max(max, currMax);
25             }
26         }
27         return max;
28     }

2.利用模型解决问题

  现在回到我们要解决的问题上去，我们利用类似于上面的方法来解决，将数组转换：

0 0 1 1 0 -> 0 0 1 1 0
0 0 1 1 0 -> 0 0 2 2 0
1 1 0 0 0 -> 1 1 0 0 0
1 1 1 0 0 -> 2 2 1 0 0

  需要注意的是，转换的规则是：每行的遍历，如果当前位置(假设nums[i][j])为true，那么dp[i][j](转换之后的数组) = dp[i - 1][j - 1]；反之，如果为false，则置为0。当i = 0时，另当别论。

  数组转换成功之后，我们只需要计算每一行的最大矩形面积，其中dp数组中0,1,2之类的表示的这个矩形的高度，当每一行的最大矩形都计算出来之后，取得最大值自然是最终的答案

 1     public int maximalRectangle(boolean[][] matrix) {
 2         if (matrix == null || matrix[0].length == 0) {
 3             return 0;
 4         }
 5         //转换之后的数组
 6         int dp[][] = new int[matrix.length][matrix[0].length];
 7         for (int i = 0; i < matrix.length; i++) {
 8             for (int j = 0; j < matrix[0].length; j++) {
 9                 if (i == 0) {
10                     //i = 0的情况
11                     dp[i][j] = matrix[i][j] ? 1 : 0;
12                 } else {
13                     //不等于0
14                     dp[i][j] = matrix[i][j] ? dp[i - 1][j] + 1 : 0;
15                 }
16             }
17         }
18         int max = 0;
19         //遍历每一行
20         for (int i = 0; i < matrix.length; i++) {
21             //取得每一行的最大值
22             int temp = findRowMax(dp[i]);
23             //更新最大值
24             max = Math.max(max, temp);
25         }
26         return max;
27     }
28 
29     private int findRowMax(int[] heights) {
30         if (heights.length == 0) {
31             return 0;
32         }
33         Stack<Integer> stack = new Stack<>();
34         stack.push(heights[0]);
35         int i = 1;
36         int max = heights[0];
37         while (i < heights.length || (i == heights.length && !stack.isEmpty())) {
38             if (i < heights.length && (stack.isEmpty() || heights[i] >= heights[stack.peek()])) {
39                 stack.push(i);
40                 i++;
41             } else {
42                 int height = heights[stack.pop()];
43                 int currMax = !stack.isEmpty() ? (i - stack.peek() - 1) * height : height * i;
44                 max = Math.max(currMax, max);
45             }
46         }
47         return max;
48     }