[NOI2013]书法家
Posted 蒟蒻ZJO :-)
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[NOI2013]书法家相关的知识,希望对你有一定的参考价值。
题目描述
小E同学非常喜欢书法,他听说NOI2013已经开始了,想题一幅“NOI”的字送给大家。
小E有一张非常神奇的纸,纸可以用一个n 行m 列的二维方格矩阵来表示,为了描述方便,我们定义矩阵左下角方格坐标为(1,1) ,右上角方格坐标为(m,n) 。矩阵的每个方格有一个整数的幸运值。在格子上面写字可以增加大家的幸运度,幸运度的大小恰好是所有被笔写到的方格的幸运值之和。现在你要在上面写上 ‘N’,‘O’,‘I’三个字母。
下面给出3个书法字的定义:
1.‘N’由若干(≥3)个边平行于坐标轴的矩形组成,设有K个矩形组成(标号1~K),第i个矩形的左下角方格坐标设为(Li ,Bi) ,右上角坐标设为(Ri ,Ti) ,要求满足:
a)Li<=Ri,Bi<=Ti
b)对任意1<i<=K,有Li=R(i-1)+1
c)对任意3<=i<K,有B(i-1)<=Ti<=T(i-1),Bi<=B(i-1);
d)B2>B1,T2=T1,B(K-1)=B(K),T(k-1)<T(K)
2.‘O’由一个大矩形A,挖去一个小矩形B得到,这两个矩形的边都平行于坐标轴。设大矩形左下角的方格坐标为(u,v),长为W宽为H,则小矩形B满足左下角方格坐标为(u+1,v+1) ,长W-2 ,宽H-2。要求满足:
a)W>=3,H>=3
b)u>R(K)+1
3.‘I’为3个边平行于坐标轴的从下到上的实心矩形组成,从下到上依次标号为1,2,3,第i 个矩形的左下角格子坐标设为(Pi , Qi ),右上角格子坐标设为(Gi , Hi ),要求满足:
a)Pi<=Gi,Qi<=Hi
b)P1=P3>u+W,G1=G3
c)Q1=H1=Q2-1,H2+1=Q3=H3
d)P1<P2<=G2<G1下图是一个‘N’,‘O’,‘I’的例子
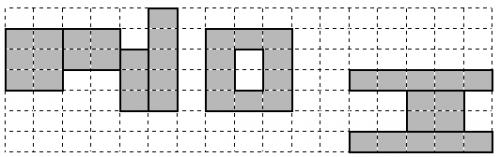
另外,所有画的图形均不允许超过纸张的边界。现在小E想要知道,他能画出的最大幸运度是多少。
输入输出格式
输入格式:
输入文件penman.in的第一行包含两个正整数n和m,分别表示矩阵的行数和列数。
接下来n行,每行有m个整数,第i+1行的第j个数表示格子(j,n-i+1)的幸运值。
输出格式:
输出到文件penman.out中,输出一个整数T,表示小E能够获得的最大幸运度。
输入输出样例
【样例输入1】 3 13 1 1 -1 -1 1 -1 1 1 1 -1 1 1 1 1 -1 1 -1 1 -1 1 -1 1 -1 -1 1 -1 1 -1 -1 1 1 -1 1 1 1 -1 1 1 1 【样例输入2】 3 13 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
【样例输出1】 24 【样例输出2】 -20
说明
样例1

样例2

数据范围
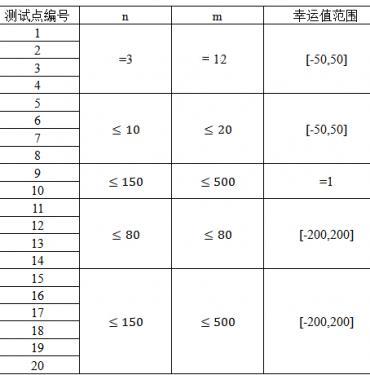
对于所有的测试数据,保证n≥3,m≥12。
超级丧病的一道题,难怪没什么人写..
首先看题就看了40分钟才懂..
好像还有一个地方题目描述和样例不吻合???
还是忽略这个细节,按样例来.
按照列来dp.
设dp[0/1][type][i][j]代表这一列选了的最上面是i,最下面是j的最大权值.
把列滚动.type表示这是第几种情况.
那么1,2,3分别表示’N’的前面一个矩形和中间一坨和后面一个矩形.
4,5,6表示’O’的.7,8,9表示’I’的.
中间还有两坨空白.
那么O和I和空白是很好搞的,直接按照题意转移即可.
主要是’N’比较难搞.
1和3其实也不难,决策单调性,可以做到n^2.
2想了半天还是只会n^3.
看了下题解,感觉有点套路..
设转移为(2,k,t)->(2,i,j),其中k<=i<=t+1,j>=t。我们将这个分成两种情况:
(1)i=t+1:设dp[t+1][t+1]=max(f[2][1][t],f[2][2][t],……,f[][2][t-1][t],f[2][t][t])。最后用dp[i][j]更新dp[i][j+1],那么直接用dp[i][j]更新当前的f[2][i][j];
(2)k<=i<=t:比如k=2,t=6,那么这个可以更新
[2,6],[2,7],……,[2,n]
[3,6],[3,7],……,[3,m]
……
[6,6],[6,7],……,[6,n]
因此设dp[i][j]=f[2][i][j],之后用dp[i][j]更新dp[i+1][j],最后再用dp[i][j]更新dp[i][j+1]即可。这两个更新的顺序不能反。反了的话就会出很多不合法的情况,这个可以手画一下.
其实就是先O(n)更新一段,再O(n)更新另一段,因为这是取最大值,所以是可以间接更新的.
1 #include<bits/stdc++.h> 2 #define inf 1000000000 3 using namespace std; 4 int f[2][10][155][155],kong[2][2],ans=-inf,a[510][510],dp[155][155]; 5 void updata(int &x,int y){x=x<y?y:x;} 6 int main(){ 7 freopen("!.in","r",stdin); 8 freopen("!.out","w",stdout); 9 int n,m; 10 scanf("%d%d",&n,&m); 11 for(int i=1;i<=n;i++) 12 for(int j=1;j<=m;j++) 13 scanf("%d",&a[j][i]),a[j][i]+=a[j][i-1]; 14 int t=0,tt=1; 15 memset(f[tt],-127/3,sizeof(f[tt])); 16 kong[tt][0]=kong[tt][1]=-inf; 17 for(int i=1;i<=m;i++){ 18 memset(f[t],-127/3,sizeof(f[t])); 19 kong[t][0]=kong[t][1]=-inf; 20 for(int j=1;j<=n;j++) 21 for(int k=j;k<=n;k++) 22 f[t][1][j][k]=f[tt][1][j][k]+a[i][k]-a[i][j-1]; 23 for(int j=1;j<=n;j++) 24 for(int k=j;k<=n;k++) 25 f[t][1][j][k]=max(f[t][1][j][k],a[i][k]-a[i][j-1]); 26 //---------------------------------------------------------第一种 27 for(int j=1;j<=n;j++){ 28 int zd=f[tt][1][j][n],sp=n; 29 for(int k=n-1;k>=j;k--){ 30 f[t][2][j][k]=zd+a[i][k]-a[i][j-1]; 31 if(f[tt][1][j][k]>zd) zd=f[tt][1][j][k],sp=k; 32 } 33 } 34 memset(dp,-127/3,sizeof(dp)); 35 for(int j=2;j<=n;j++) 36 for(int k=1;k<j;k++) 37 updata(dp[j][j],f[tt][2][k][j-1]); 38 for(int j=1;j<=n;j++) 39 for(int k=j+1;k<=n;k++) 40 updata(dp[j][k],dp[j][k-1]); 41 for(int j=1;j<=n;j++) 42 for(int k=j;k<=n;k++) 43 updata(f[t][2][j][k],dp[j][k]+a[i][k]-a[i][j-1]); 44 for(int j=1;j<=n;j++) 45 for(int k=j;k<=n;k++) 46 dp[j][k]=f[tt][2][j][k]; 47 for(int j=1;j<=n;j++) 48 for(int k=1;k<j;k++) 49 updata(dp[k+1][j],dp[k][j]); 50 for(int j=1;j<=n;j++) 51 for(int k=j;k<=n;k++) 52 updata(dp[j][k+1],dp[j][k]); 53 for(int j=1;j<=n;j++) 54 for(int k=j;k<=n;k++) 55 updata(f[t][2][j][k],dp[j][k]+a[i][k]-a[i][j-1]); 56 //---------------------------------------------------------第二种 57 for(int k=n;k>1;k--){ 58 int zd=f[tt][2][k][k],sp=k; 59 for(int j=k-1;j>=1;j--){ 60 f[t][3][j][k]=zd+a[i][k]-a[i][j-1]; 61 if(f[tt][2][j][k]>zd) zd=f[tt][2][j][k],sp=j; 62 } 63 } 64 for(int j=1;j<=n;j++) 65 for(int k=j;k<=n;k++) 66 updata(f[t][3][j][k],f[tt][3][j][k]+a[i][k]-a[i][j-1]); 67 //---------------------------------------------------------第三种 68 int zd=kong[tt][0]; 69 for(int j=1;j<=n;j++) 70 for(int k=j;k<=n;k++) 71 updata(zd,f[tt][3][j][k]); 72 kong[t][0]=zd; 73 //---------------------------------------------------------N O 之间的空 74 for(int j=1;j<=n;j++) 75 for(int k=j+2;k<=n;k++) 76 f[t][4][j][k]=kong[tt][0]+a[i][k]-a[i][j-1]; 77 //---------------------------------------------------------O 的第一部分 78 for(int j=1;j<=n;j++) 79 for(int k=j+2;k<=n;k++){ 80 updata(f[t][5][j][k],f[tt][4][j][k]+a[i][k]-a[i][k-1]+a[i][j]-a[i][j-1]); 81 updata(f[t][5][j][k],f[tt][5][j][k]+a[i][k]-a[i][k-1]+a[i][j]-a[i][j-1]); 82 } 83 //---------------------------------------------------------O 的第二部分 84 for(int j=1;j<=n;j++) 85 for(int k=j+2;k<=n;k++) 86 f[t][6][j][k]=f[tt][5][j][k]+a[i][k]-a[i][j-1]; 87 //---------------------------------------------------------O 的第三部分 88 zd=kong[tt][1]; 89 for(int j=1;j<=n;j++) 90 for(int k=j;k<=n;k++) 91 updata(zd,f[tt][6][j][k]); 92 kong[t][1]=zd; 93 //---------------------------------------------------------N O 之间的空 94 for(int j=1;j<=n;j++) 95 for(int k=j+2;k<=n;k++){ 96 int tmp=a[i][k]-a[i][k-1]+a[i][j]-a[i][j-1]; 97 f[t][7][j][k]=kong[tt][1]+tmp; 98 updata(f[t][7][j][k],f[tt][7][j][k]+tmp); 99 } 100 //---------------------------------------------------------I 的第一部分 101 for(int j=1;j<=n;j++) 102 for(int k=j+2;k<=n;k++){ 103 int tmp=a[i][k]-a[i][j-1]; 104 f[t][8][j][k]=f[tt][7][j][k]+tmp; 105 updata(f[t][8][j][k],f[tt][8][j][k]+tmp); 106 } 107 //---------------------------------------------------------I 的第二部分 108 for(int j=1;j<=n;j++) 109 for(int k=j+2;k<=n;k++){ 110 int tmp=a[i][k]-a[i][k-1]+a[i][j]-a[i][j-1]; 111 f[t][9][j][k]=f[tt][8][j][k]+tmp; 112 updata(f[t][9][j][k],f[tt][9][j][k]+tmp); 113 updata(ans,f[t][9][j][k]); 114 } 115 swap(t,tt); 116 } 117 printf("%d",ans); 118 return 0; 119 }
以上是关于[NOI2013]书法家的主要内容,如果未能解决你的问题,请参考以下文章