查找应用篇
Posted 樱桃挚爱丸子
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了查找应用篇相关的知识,希望对你有一定的参考价值。
查找
一、查找的基本概念
1、动态查找表在查找过程中插入元素或者从查找表中删除元素,
2、静态查找表只是查找特定元素或者检索特定元素的属性。
3、通俗的说,动态查找表可以对查找表结构进行修改,而静态查找表只是查询。
4、顺序存储和链式存储方式都支持线性查找。
5、二分查找时,数据必须以顺序方式查找,而且必须有序。若是链式存储,则只能支持顺序查找。若是数据无序,则不能二分查找。
6、要进行散列查找,则元素必须以散列方式进行存储。
二、顺序查找法
1、顺序查找的算法
1)数组实现
采用顺序表来存储线性表,实现顺序查找算法
#include"SeqList.h"
int SeqSearch(SeqList &L, DataType x)
{
int i = 0;
DataType temp;
while(i<L.n && L.data[i] != x)
i++;
if(i == L.n)
return 0;
else
{
if(i > 0)
{
temp = L.data[i-1];
L.data[i-1] = L.data[i];
L.data[i] = temp;
return i;
}
}
}
2)链表实现
采用带头借点的线性链表存储线性表,实现顺序查找算法
#include"LinkList.h"
LinkNode *LinkSearch(LinkList &L, DataType x)
{
LinkNode *p = l-> Link,
*pre = L, *ppre = NULL;
while(p != NULL && p->data != x)
{
ppre = pre;
pre = p;
p = p->link;
}
if(p != NULL && pre != L)
{
pre->link = p->link;
p->link = pre;
ppre->link = p;
}
return p;
}
2、顺序查找不论在顺序线性表中还是在链式线性表中的时间复杂度为O(n)
三、折半查找法
1、折半查找的算法
设计一个递归算法,实现在有序顺序表上的折半查找
int binarySearch(seqLIst &L, DataType x, int left, int right)
{
int mid = -1;
if(left <= right)
{
mid = (left+right)/2;
if(x > data[mid])
mid = binarySearch(L, x, mid+1, right);
else if(x < data[mid])
mid = binarySearch(L, x, left, mid-1);
}
return mid;
};
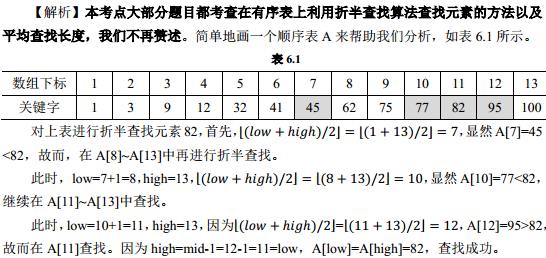
2、有一个有序表为{1, 3, 9, 12, 32, 41, 45, 62, 75, 77, 82, 95,100},当折半查找值为 82 的结点时,
4 次比较后查找成功。
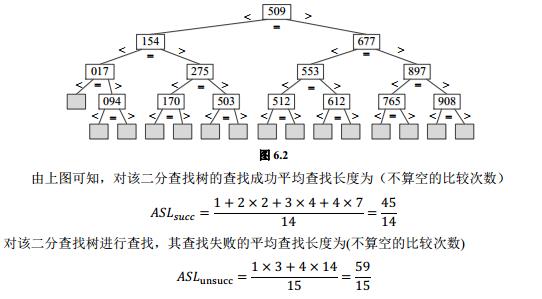
3、设有序顺序表中的元素依次为 017, 094, 154, 170, 275, 503, 509, 512,553, 612, 677, 765, 897, 908。试画出
对其进行折半搜索时的二叉搜索树(即二分查找树),并计算搜索成功的平均搜索长度和搜索不成功的平均搜索长度。
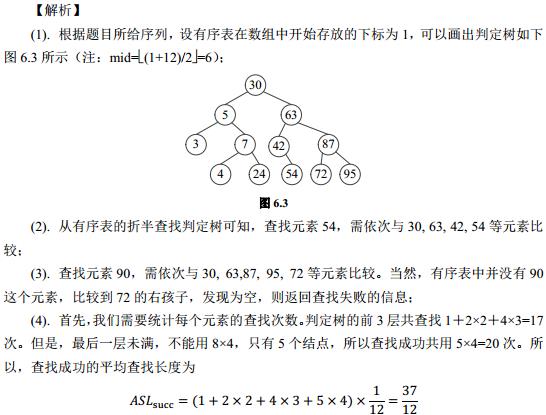
4、假定对有序表:(3, 4, 5, 7, 24, 30, 42, 54, 63, 72, 87, 95)进行折半查找,试回答下列问题:
(1). 画出描述折半查找过程的判定树;
(2). 若查找元素 54,需依次与哪些元素比较?
(3). 若查找元素 90,需依次与哪些元素比较?
(4). 假定每个元素的查找概率相等,求查找成功时的平均查找长度。
四、散列表
1、散列表基本概念
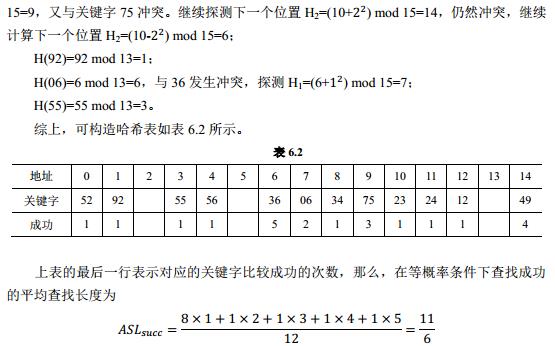
散列表,它在元素的存储位置与元素关键码间建立一个确定的对应函数关系,使每个关键码与结构中的一个唯一的存储位置相对应 常见的散列函数 定义域必须包括需要存储的全部关键码,其值域必须在0到m-1之间 1、直接定址法 hash(key) = a*key+b 2、除留余数法 设散列表中允许的地址范围为0 ~m-1,取一个不大于m,但是最接近于或等于m的质数p作为除数,利用公式hash(key) = key % p(p<=m),要求这时的质数p不是接近2的幂的数、 解决冲突的开地址法 1、线性探测 使用某一个散列函数计算出初始散列地址,一旦发生冲突,在表中顺次向后寻找下一个空闲位置的公式为 2、二次探测 使用二次探测法,在表中寻找“下一个”空闲位置的公式 解决冲突的拉链法 例如设给出一组元素的关键码为37,25,14,36,49,68,57,11,取m = 11,采取拉链法解决冲突,散列函数为Hash(x) = x % 11,则各关键码计算出的地址为 散列表的装填因子@的定义为; @ = 表中已装有的记录数n/表中预设的最大记录数m
2、

3、

4、

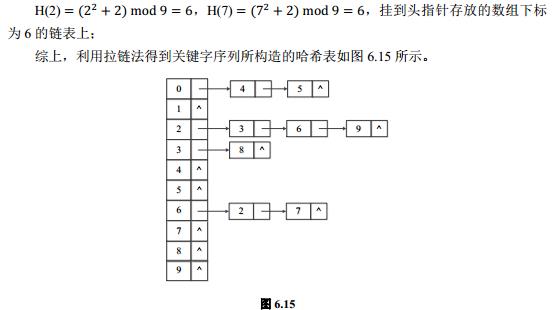
以上是关于查找应用篇的主要内容,如果未能解决你的问题,请参考以下文章
Android 插件化VirtualApp 源码分析 ( 目前的 API 现状 | 安装应用源码分析 | 安装按钮执行的操作 | 返回到 HomeActivity 执行的操作 )(代码片段