子数组最大值设计02

Posted 2020-06-29

设计思路：

才过几天就有了新挑战，我真是找不到多少时间看数学了，下面是新任务的大致意思：

输入一个整形数组，数组里有正数也有负数。数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和，如果数组A[0]……A[j-1]首尾相邻，允许A[i-1]，…… A[n-1]，A[0]……A[j-1]之和最大，求最大子数组的和最大子数组的位置。

刚开始看这道题，看的我云里雾里的，觉得是看懂了，又感到有些迷惑，所以就简单把数组看成环形，然后想只要循环两圈不就解决了吗！so我开始如下的解题过程

 

求解过程：

这是上次的解题思路：

数组形式:a[0],a[1],a[2],a[3]........a[n-1],a[n]

总共可以看成求子过程最优，共两种情况：

把b[]=max(a[0]+a[1]+...a[i-1])看成到i元素的(i-1)子数组最大值

If(b[]<0)这样a[i]+b[]<a[i] 则最大换为a[i]

If(b[]>=0)a[i]+b[]>a[i] 最大换为a[i]+b[]

基础上记入头尾然后再循环一次，结束位置在第一次结束的元素之前一个元素。

 

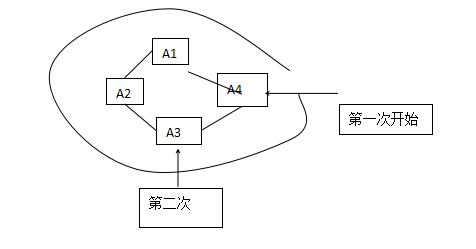
如下是第一次考虑的错误代码（请不要直接复制）：

 

 1 //实现数组的首尾相连 再求子数组的和最大值以及子数组的位置
 2 #include<iostream>
 3 using namespace std;
 4 
 5 int main()
 6 {
 7     /*求子数组的和
 8     输入整形数组，数组里有正数有负数，连续数字构成子数组
 9     求子数组最大值O(n)
10     */
11     //解题用动态规划求最优子结构
12 
13     cout<<"请输入数组元素个数："<<endl;
14     int num;  //数组元素个数
15     cin>>num;
16     int a[100]={0}; 
17     for(int i=0;i<num;i++)
18         cin>>a[i];    //输入数组元素
19 
20     //考虑首尾相连时改变数组结束判断的位置
21 
22     //动态求解
23     int b[100][100]={0};
24     b[0][0]=0;      //初始子数组和
25     b[0][1]=a[0];    //a[i]数的值
26     for(int i=1;i<num;i++)
27     {
28         if(b[i-1][0]>=0)
29             b[i][0]=b[i-1][0]+b[i-1][1];
30         else
31             b[i][0]=b[i-1][1];
32         b[i][1]=a[i];
33     }
34     //加上最后一个数(第一次迭代的结果)
35     if(b[num-1][0]>=0)
36         b[num][0]=b[num-1][0]+b[num-1][1];
37     else
38         b[num][0]=b[num-1][1];
39     b[num][1]=a[0];     //循环（首尾连）
40 
41     //二次迭代
42     for(int i=1;i<num;i++)
43     {
44         if(b[num+i-1][0]>=0)
45             b[num+i][0]=b[num+i-1][0]+b[num+i-1][1];
46         else
47              b[num+i][0]=b[num+i-1][1];
48         b[num+i][1]=a[i];
49 
50     }
51     //比较各个子数组最大的求出值
52     int max=b[0][0];
53     for(int i=1;i<=(num+num-1);i++)
54     {
55         if(b[i][0]>max)
56             max=b[i][0];
57     }
58     cout<<"子数组和最大值为："<<max<<endl;
59     return 0;
60 }

 

可能大家看到这就感觉有问题了，我也感觉有问题，但是说不上，但举个例子就明白了，

-1，2，3 结果是6 但答案肯定是5，因为在循环过程中重复使用数组元素，所以这样的算法有问题，得换个思维：

其实这个循环过程就是每次nun个数的求解

所以把上述的数组看成-1 2 3 -1 2,看到这大家的思路肯定更清醒了，只要依次求解每次循环中子数组最大，再比较就好了

如下为正确代码：

 

  1 //实现数组的首尾相连 再求子数组的和最大值以及子数组的位置
  2 #include<iostream>
  3 #include<queue>
  4 #include<string>
  5 #include<sstream>
  6 using namespace std;
  7 
  8 int main()
  9 {
 10     /*求子数组的和
 11     输入整形数组，数组里有正数有负数，连续数字构成子数组
 12     求子数组最大值O(n)
 13     */
 14     //解题用动态规划求最优子结构
 15 
 16     queue<int> q=queue<int>();    //建立队列来循环数组
 17     string k[100][100];    //记录子数组最大位置
 18     cout<<"请输入数组元素个数："<<endl;
 19     int num;  //数组元素个数
 20     cin>>num;
 21     int a[100]={0}; 
 22     int i=0,j=0;
 23     cout<<"请输入数组元素："<<endl;
 24     for(i=0;i<num;i++)
 25         cin>>a[i];    //输入数组元素
 26 
 27     //考虑首尾相连时改变数组结束判断的位置
 28     //将n-1个数组元素放到数组尾部形成新数组
 29 
 30     for(j=0;j<num-1;j++)
 31     {
 32         q.push(a[j]);
 33     }
 34     for(j=0;j<num-1;j++)
 35     {
 36         a[num+j]=q.front();
 37         q.pop();
 38     }
 39     
 40     
 41     //动态数组求解
 42     int b[100][100][2]={0};
 43     i=0;j=0;
 44     for(i=0;i<num;i++)
 45     {
 46         b[i][0][0]=0;      //初始子数组和
 47         b[i][0][1]=a[i];    //a[i]数的值
 48         k[i][0]="";
 49         for(j=1;j<num;j++)
 50         {
 51           stringstream ss;
 52         if(b[i][j-1][0]>=0)     
 53         {
 54             
 55             b[i][j][0]=b[i][j-1][0]+b[i][j-1][1];
 56             ss<<((i+j-1)%num);
 57             ss>>k[i][j];      //写入位置字符数组
 58 
 59             k[i][j]=k[i][j-1]+k[i][j];
 60         }
 61         else
 62         {
 63             b[i][j][0]=b[i][j-1][1];
 64             ss<<((i+j-1)%num);
 65             ss>>k[i][j];    
 66             
 67         }
 68 
 69         b[i][j][1]=a[i+j];
 70         }
 71         stringstream ss;
 72         //加上最后一个数
 73     if(b[i][num-1][0]>=0)
 74     {
 75         b[i][num][0]=b[i][num-1][0]+b[i][num-1][1];
 76         ss<<((i+j-1)%num);
 77         ss>>k[i][num];
 78         k[i][num]=k[i][num-1]+k[i][num];
 79     }
 80     else
 81     {
 82         b[i][num][0]=b[i][num-1][1];
 83         ss<<((i+j-1)%num);
 84         ss>>k[i][num];
 85     }
 86 
 87     }
 88     
 89 
 90     //比较各个子数组最大的求出值
 91     int max=b[0][0][0];
 92     int max_i=0;   //记录最大值的坐标
 93     int max_j=0;
 94     for(i=0;i<num;i++)
 95     {
 96         for(j=0;j<=num;j++)
 97         {
 98         if(b[i][j][0]>max)
 99         {
100             max=b[i][j][0];  
101             max_i=i;
102             max_j=j;
103         }
104         }
105     }
106     cout<<"子数组和最大值为："<<max<<endl;
107 
108     int si=0,sl=0;
109     cout<<"最大子数组各元素数组中的位置为（以0开始）：";
110     if(k[max_i][max_j].size()==1)
111             cout<<k[max_i][max_j]<<endl;
112     else
113     {
114         si=k[max_i][max_j].size();
115         while(si--)
116         {
117             cout<<k[max_i][max_j][sl++]<<" ";
118         }
119     }
120     cout<<endl;
121         return 0;
122 }

 运行代码：

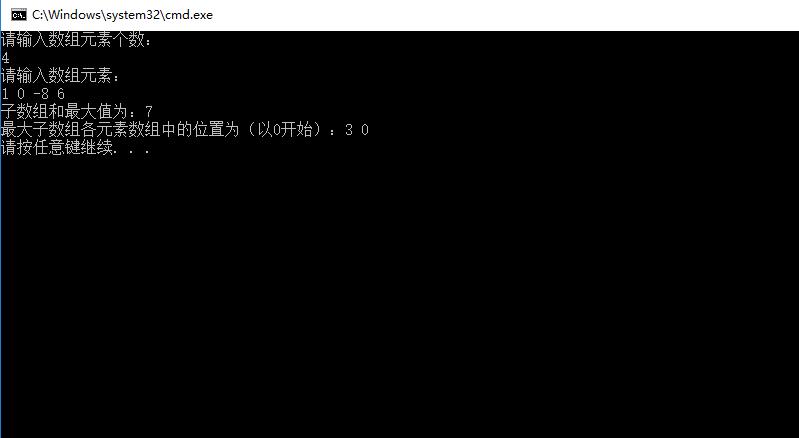
求解总结

看问题必须要通过一些实例的验证才能确保是正确无误后，才能正确入手，保证结果正确性。

Ps:同组的另一战友的博客

http://www.cnblogs.com/brucekun/p/5321247.html