逻辑回归(logistic回归)
Posted steed
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了逻辑回归(logistic回归)相关的知识,希望对你有一定的参考价值。
前言
以下内容是个人学习之后的感悟,转载请注明出处~
逻辑回归
一、为什么使用logistic回归
一般来说,回归不用在分类问题上,因为回归是连续型模型,而且受噪声影响比较大。
Why? 为什么回归一般不用在分类上?其实,很多初学者都会提出这个问题。然而,文字的解释往往不能说服我们,接下来
用图示的方式为大家讲解。
以最简单的分类为例,当y≥0.5时,输出“1”;当y<0.5时,输出“0”。下面左图,数据样本较好,线性回归模型在y=0.5处的橘色分界线
刚好在“0”、“1”两类样本的分界线处,完美地完成分类。然而,现实情况往往没有这么乐观,下面有图中出现了一个额外的样本,所谓的噪
声点,会使训练完毕的线性回归模型准确度变差。从右图中可以做直观地看到,线性回归模型在y=0.5处的粉色分界线将一个“1”类样本分类到
了“0”类样本集中,此时就出现了判断失误。
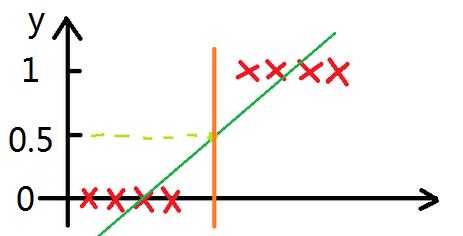

所以线性回归一般不用在分类问题上,如果非要用于分类,可以使用logistic回归。
逻辑回归为什么可以用在分类上?why?
原因很简单,逻辑回归本质上是线性回归,只是在特征到结果的映射中加入了一层函数映射,即先把特征线性求和θTx,设为z,然后使用函
数g(z)作为假设函数来预测。g(z)可以将连续值映射到0和1上。如下图所示,当z≥0时,输出为1;当z<0时,输出为0。这样可以实现很好的分类。
具体实现请看下文~
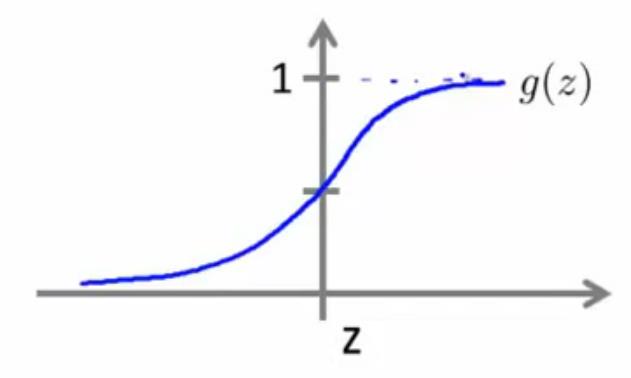
二、logistic回归
- 假设函数:
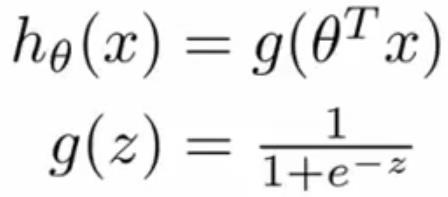
- 初始代价函数:
![]()
(细心的童鞋会发现,这里的代价函数与线性回归模型中的J(θ0,θ1)不一样,其实就是整体误差和平均误差的区别。)
显然,由于S型函数的存在,代价函数是非凸函数,无法使用梯度下降法来求极小值。这就需要转换为下面的简易代价函数。
- 简易代价函数:
说实话,这一步,我也不知道是怎么推导的,有哪位大神知道的话,请不吝赐教~
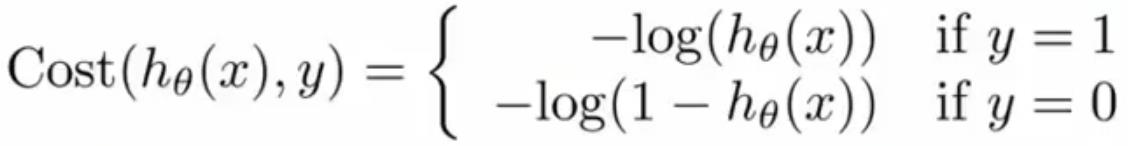
然而,要想使用梯度下降法,还需要转换为J(θ)代价函数
- J(θ)代价函数(凸函数):

- 使用方法:
1、采用梯度下降法,不断迭代下列公式,直到收敛,求出θ。
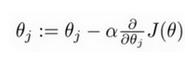
![]()
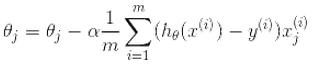
其推导过程如下:
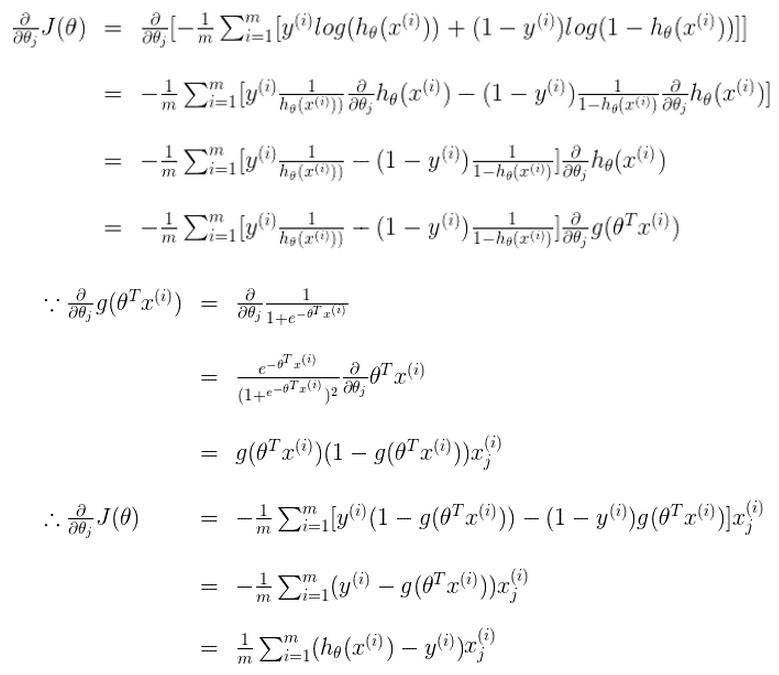
细心的童鞋可能会注意到,逻辑回归和线性回归在梯度下降法中使用的迭代公式竟然一样。其实不然,不同点在于
迭代公式中的hθ(x):
逻辑回归: 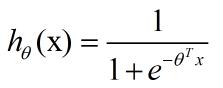
线性回归: ![]()
2、判断θTx的大小来分类。
“y=1”,当θTx≥0
“y=0”,当θTx<0
(很容易发现θTx=0是分类的决策边界)
三、多分类逻辑回归
使用逻辑回归算法进行多分类时,可以设其中一类为1,其他都为0,建立一个分类器,以此类推,遍历全部类别,建立N个分类器。
如下表所示,总共3个类别,因此设立3个分类器,每个分类器的样本训练由上文中的二分类步骤完成。
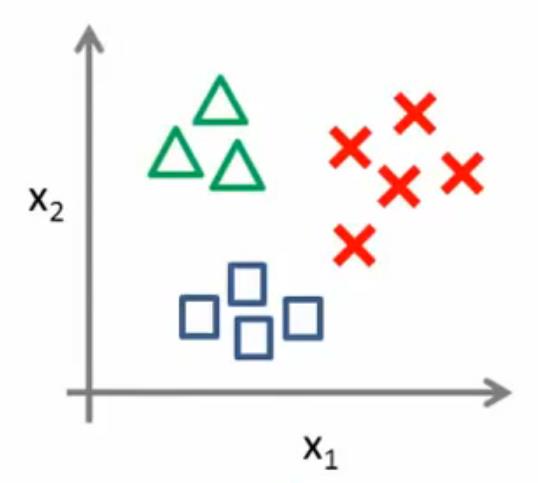 |
 |
三角形设为1,其他设为0。作为分类器1,即hθ(1)(x) |
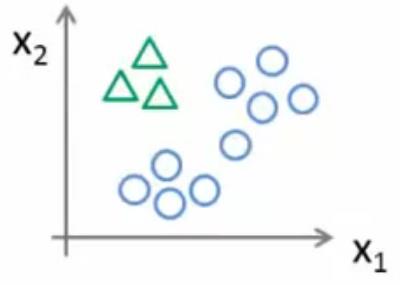
 |
正方形设为1,其他设为0。作为分类器2,即hθ(2)(x) | |
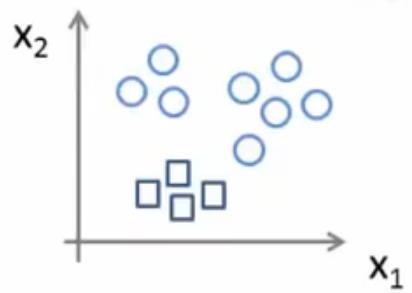
 |
红十字设为1,其他设为0。作为分类器3,即hθ(3)(x) |
每个分类器训练完毕后,取一个新的x数据,代入3个分类器中,哪个求出的h值最大,则这个分类器可信度最高,此分类器的“1”类别
就是此x的类别。
以上是全部内容,如果有什么地方不对,请在下面留言,谢谢~
以上是关于逻辑回归(logistic回归)的主要内容,如果未能解决你的问题,请参考以下文章