p1164立方体求和

Posted 2020-10-03 Shadow

 

　　题目：

SubRaY有一天得到一块西瓜,是长方体形的....
SubRaY发现这块西瓜长m厘米,宽n厘米,高h厘米.他发现如果把这块西瓜平均地分成m*n*h块1立方厘米的小正方体,那么每一小块都会有一个营养值(可能为负,因为西瓜是有可能坏掉的,但是绝对值不超过200).
现在SubRaY决定从这m*n*h立方厘米的西瓜中切出mm*nn*hh立方厘米的一块小西瓜(一定是立方体形,长宽高均为整数),然后吃掉它.他想知道他最多能获得多少营养值.(0<=mm<=m,0<=nn<=n,0<=hh<=h.mm,nn,hh的值由您来决定).
换句话说,我们希望从一个m*n*h的三维矩阵中,找出一个三维子矩阵,这个子矩阵的权和最大.

 

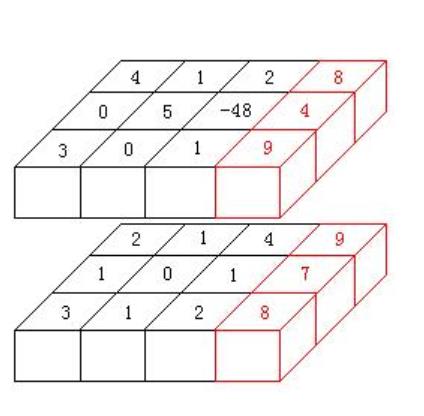
一个2*3*4的例子,最优方案为切红色2*3*1部分

输入格式 Input Format
首行三个数h,m,n(注意顺序),分别表示西瓜的高,长,宽.
以下h部分,每部分是一个m*n的矩阵,第i部分第j行的第k个数表示西瓜第i层,第j行第k列的那块1立方厘米的小正方体的营养值.

输出格式 Output Format
SubRaY所能得到的最大营养值

样例输入 Sample Input
2 3 4
4 1 2 8
0 5 -48 4
3 0 1 9
2 1 4 9
1 0 1 7
3 1 2 8

样例输出 Sample Output
45

时间限制 Time Limitation
1s

注释 Hint
对于30%的数据,h=1,1<=m,n<=10
对于全部的数据,1<=h<=32,1<=m,n<=50,保证h<=m,n

来源 Source
noip 模拟赛

 

　　　　因为数据比较小，所以不会超时的。你先处理下这一层这个位置和上个位置的累加和，然后在处理每一列的累加和。

　　　然后每次运算只用从左开始往右进行累加，算的就是一个矩阵了。

　　　　

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int a[52][52][52];
int c[52][52][52];
int b[1000];
int p[1000];
int main()
{
    int h,m,n;//高，长，宽
    cin>>h>>m>>n;
    for(int w=1;w<=h;w++)
    {
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
                cin>>a[w][i][j],c[w][i][j]=a[w][i][j];
        }
    }
    for(int w=1;w<=h;w++)
    {
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
            {
                c[w][i][j]+=c[w-1][i][j];
            }
        }
    }
    for(int w=1;w<=h;w++)
    {
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
            {
                c[w][i][j]+=c[w][i-1][j];
            }
        }
    }
    /*cout<<endl;
    for(int w=1;w<=h;w++)
    {
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
            {
                cout<<c[w][i][j]<<\' \';
            }
            cout<<endl;
        }
    }*/
    int ans=0;
    for(int w=1;w<=h;w++)//第几层
    {
        for(int H=1;H<=w;H++)//w层上面选几层
        {
            for(int i=1;i<=m;i++)//第i行
            {
                for(int t=1;t<=i;t++)//这行上面的t行
                {
                    memset(b,0,sizeof(b));
                    memset(p,0,sizeof(p));
                    for(int k=1;k<=n;k++)//从左往右加
                    {
                        p[k]=c[w][i][k]-c[H-1][i][k]-c[w][t-1][k]+c[H-1][t-1][k];
                        b[k]=max(b[k-1]+p[k],p[k]);
                        if(b[k]>ans)
                            ans=b[k];
                    }
                }
            }
        }
    }
    cout<<ans<<endl;
    return 0;
}

程序里有标注