求逆序数数目（树状数组+离散化）

Posted 2020-10-02 DearDongchen

 

404在玩忍者印记(Mark of the Ninja)操纵忍者时遇到这样一个场景，两栋大楼之间有许多绳索，从侧面看，就像这个样子:

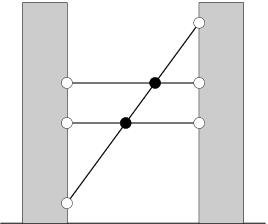
我们的忍者非常有好奇心，他可以观察到每个绳索的端点在两栋楼的高度，想知道这些绳索有多少个交点（图中黑色的点）。他观察到不会建筑上不会有一点上有两个绳索，并且没有三条绳索共点。

输入描述

第一行：整数T,代表有T组数据。 (1 <= T <= 100)

下一行：整数N,代表有N条绳索。 (1 <= N <= 100000)

接下来Na行给出两个整数A_i, B_i,分别代表绳索端点在左右两边大楼的高度。

0 <= A_i,B_i <= 1000000000

输出描述

Case #x: y

x代表样例组数，从1开始。

y代表绳索交点数。

样例输入

2
3
1 10
5 5
7 7
2
1 1
2 2

样例输出

Case #1: 2
Case #2: 0

树状数组高效求出逆序对，点的数目少，数值可能很大，所以用了离散化处理

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
using namespace std;
const int maxn= 1e5+7;
int sum[maxn], arr[maxn], k;
struct Edge{
    int a, b;
    bool operator < (const Edge t)const{
        if(a != t.a)
            return a < t.a;
        return b < t.b;
    }
}edge[maxn];
int lowbit(int x){
    return -x & x;
}
void add(int i, int val){
    while(i <= maxn){
        sum[i] += val;
        i += lowbit(i);
    }
}
int Sum(int i){
    int s = 0;
    while(i){
        s += sum[i];
        i -= lowbit(i);
    }
    return s;
}
int bisearch(int key, int n){

    int l = 1, r = n;
    while(l <= r){
        int m = (l + r)/2;
        if(arr[m] == key)
            return m;
        if(arr[m] < key)
            l = m + 1;
        else
            r = m - 1;
    }
    //
}
int main(){
    //freopen("in.txt", "r", stdin);
    int t;
    scanf("%d", &t);
    int kase = 1;
    while(t--){
        scanf("%d", &k);
        for(int i = 0; i < k; i++){
            scanf("%d%d", &edge[i].a, &edge[i].b);
            arr[i+1] = edge[i].b;
        }
        sort(arr+1, arr+k+1);
        int m = 2;
        for(int i = 2; i < k; i++){
            if(arr[i] != arr[i-1]){
                arr[m++] = arr[i];
            }
        }
        sort(arr+1, arr+m+1);
        sort(edge, edge+k);
        memset(sum, 0, sizeof(sum));
        long long ans = 0;
        for(int i = 0; i < k; i++){
            int lisan = bisearch(edge[i].b, m);
            add(lisan, 1);
            ans += Sum(m) - Sum(lisan);
            //printf("%d\\n", lisan);
        }
        printf("Case #%d: ", kase++);
        printf("%lld\\n", ans);
    }
    return 0;
}