数据结构14——AC自动机

Posted 2020-10-02 GGBeng

一、相关介绍

知识要求

1. 字典树Trie
2. KMP算法

AC自动机

• 多模式串的字符匹配算法（KMP是单模式串的字符匹配算法）

单模式串问题&多模式串问题

• 单模就是给你一个模式串，问你这个模式串是否在主串中出现过，这个问题可以用kmp算法高效完成；
• 多模就是给你多个模式串，问你有多少个模式串在这个主串中出现过。

若我们暴力地用每一个模式串对主串做kmp，这样虽然理论上可行，但是时间复杂度非常之高。而AC自动机算法就能高效地处理这种多模式串问题。

 

二、算法实现

【打基础】

失配指针fail

• 每个节点都有一个失配指针fail
• 指向以当前节点表示的字符为最后一个字符的最长当前字符串的后缀字符串的最后一个节点

假如我们有四个单词：abcd, bce, abd, cd，那么我们建立字典树如下：

 

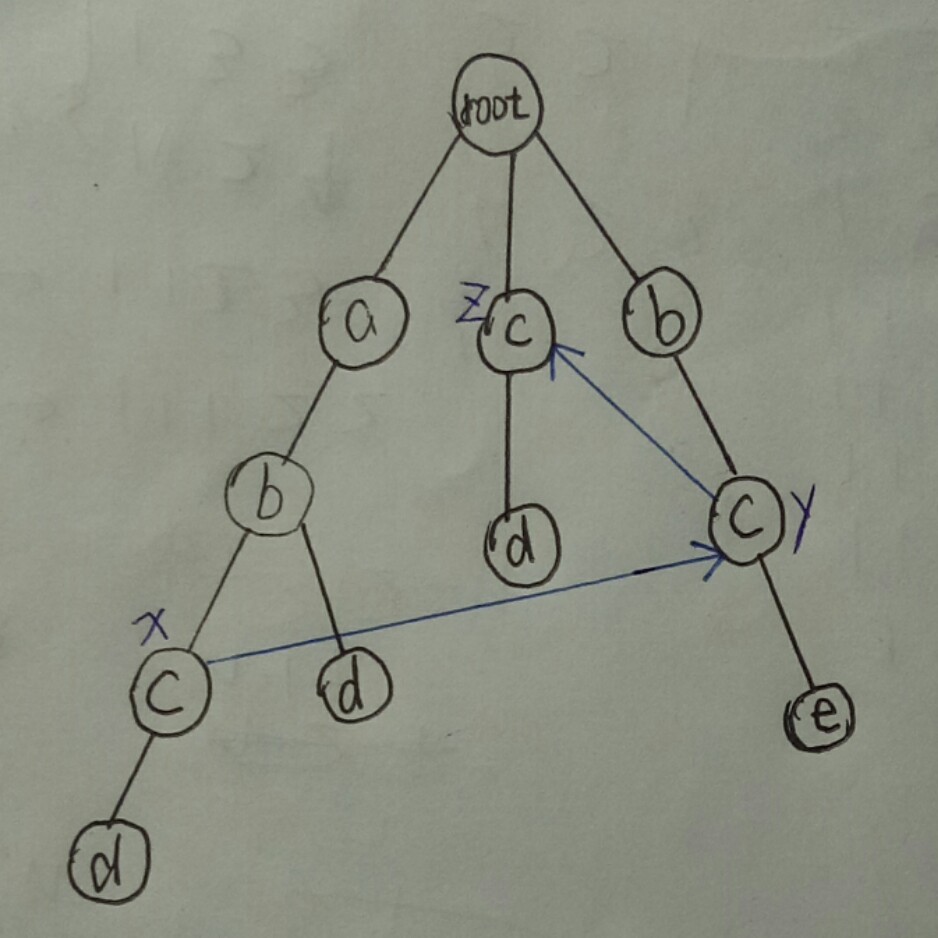
首先我们让与根节点直接相连的节点的fail直接指向root,为了让你更好的理解fail指针，我们以节点x,y,z为例，我们让从图中我们可以看出x节点的fail指向了y节点，y节点的fail指向了z节点，为什么会这样指，因为x节点表示字符串abc,而字典树中含有最长，且以c结尾，且是abc的后缀的字符串bc(以y节点结尾的），同理，以y节点表示的字符串是bc,而以c结尾，且是bc的后缀的最长字符串是c（以z节点结尾的）。这就是fail指针指向的目标，那么我们得到了这个fail指针在匹配中有什么用呢，我们还是用上面的那个图来举例说明一下，假设文本串是abce,通过字典树我们可以看出，通过abc,所以我们可以匹配到x节点，但是到后面，我们发现d与e不匹配，这时我们就需要用到当前节点的fail了，因为x的fail指向的是y节点，所以我们直接跳到y节点，这是发现y节点后面有e，匹配上了，所以单词bce就在文本串abce中被检测出来了。

 

【AC自动机简述】

• Trie的每个节点加上了一个fail指针，fail指针指向当前匹配失败的跳转位置，这个类似于KMP的next数组。

【AC自动机的构造】

• ①把所有的模式串建立一棵Trie；（作为AC自动机的搜索数据结构）

在建立字典树之前，我们先定义每个字典树上节点的结构体变量：

struct node{
    node *next[26];
    node *fail;　　　　//失配指针
    int sum;　　　　　 //这个节点是不是一个单词的结尾，以及相应的个数。
};

建立字典树代码：

void Insert(char *s)
{
    node *p = root;
    for(int i = 0; s[i]; i++)
    {
        int x = s[i] - \'a\';
        if(p->next[x] == NULL)
        {
            newnode=(struct node *)malloc(sizeof(struct node));
            for(int j=0;j<26;j++) newnode->next[j] = 0;
            newnode->sum = 0;newnode->fail = 0;
            p->next[x]=newnode;
        }
        p = p->next[x];
    }
    p->sum++;
}

注意：在建立字典树的过程中，先让每个节点的fail指针先为空 。

• ②构造fail指针，使当前字符失配时跳转到具有最长公共前后缀的字符继续匹配。如同KMP算法一样， AC自动机在匹配时如果当前字符匹配失败，那么利用fail指针进行跳转。由此可知如果跳转，跳转后的串的前缀，必为跳转前的模式串的后缀并且跳转的新位置的深度（匹配字符个数）一定小于跳之前的节点。所以我们可以利用 bfs在Trie上面进行fail指针的求解；

下面是构造fail指针的具体代码（基于队列（bfs）实现）：

void build_fail_pointer()
{
    head = 0;
    tail = 1;
    q[head] = root;
    node *p;
    node *temp;
    while(head < tail)
    {
        temp = q[head++];
        for(int i = 0; i <= 25; i++)
        {
            if(temp->next[i])
            {
                if(temp == root)
                {
                    temp->next[i]->fail = root;
                }
                else
                {
                    p = temp->fail;
                    while(p)
                    {
                        if(p->next[i])
                        {
                            temp->next[i]->fail = p->next[i];
                            break;
                        }
                        p = p->fail;
                    }
                    if(p == NULL) temp->next[i]->fail = root;
                }
                q[tail++] = temp->next[i];
            }
        }
    }
}

• ③扫描主串进行匹配。

最后是利用前面求得的fail指针进行匹配。 
代码如下：

void ac_automation(char *ch)
{
    node *p = root;
    int len = strlen(ch);
    for(int i = 0; i < len; i++)
    {
        int x = ch[i] - \'a\';
        while(!p->next[x] && p != root) p = p->fail;
        p = p->next[x];
        if(!p) p = root;
        node *temp = p;
        while(temp != root)
        {
           if(temp->sum >= 0)
           {
               cnt += temp->sum;
               temp->sum = -1;
           }
           else break;
           temp = temp->fail;
        }
    }
}

【AC自动机详讲】

我们给出5个单词，say，she，shr，he，her。给定字符串为yasherhs。问多少个单词在字符串中出现过。

一、Trie

首先我们需要建立一棵Trie。但是这棵Trie不是普通的Trie，而是带有一些特殊的性质。

首先会有3个重要的指针，分别为p, p->fail, temp。

1.指针p，指向当前匹配的字符。若p指向root，表示当前匹配的字符序列为空。（root是Trie入口，没有实际含义）。

2.指针p->fail，p的失败指针，指向与字符p相同的结点，若没有，则指向root。

3.指针temp，测试指针（自己命名的，容易理解！~），在建立fail指针时有寻找与p字符匹配的结点的作用，在扫描时作用最大，也最不好理解。

对于Trie树中的一个节点，对应一个序列s[1...m]。此时，p指向字符s[m]。若在下一个字符处失配，即p->next[s[m+1]] == NULL，则由失配指针跳到另一个节点(p->fail)处，该节点对应的序列为s[i...m]。若继续失配，则序列依次跳转直到序列为空或出现匹配。在此过程中，p的值一直在变化，但是p对应节点的字符没有发生变化。在此过程中，我们观察可知，最终求得得序列s则为最长公共后缀。另外，由于这个序列是从root开始到某一节点，则说明这个序列有可能是某些序列的前缀。

再次讨论p指针转移的意义。如果p指针在某一字符s[m+1]处失配(即p->next[s[m+1]] == NULL)，则说明没有单词s[1...m+1]存在。此时，如果p的失配指针指向root，则说明当前序列的任意后缀不会是某个单词的前缀。如果p的失配指针不指向root，则说明序列s[i...m]是某一单词的前缀，于是跳转到p的失配指针，以s[i...m]为前缀继续匹配s[m+1]。

对于已经得到的序列s[1...m]，由于s[i...m]可能是某单词的后缀，s[1...j]可能是某单词的前缀，所以s[1...m]中可能会出现单词。此时，p指向已匹配的字符，不能动。于是，令temp = p，然后依次测试s[1...m], s[i...m]是否是单词。

构造的Trie为：

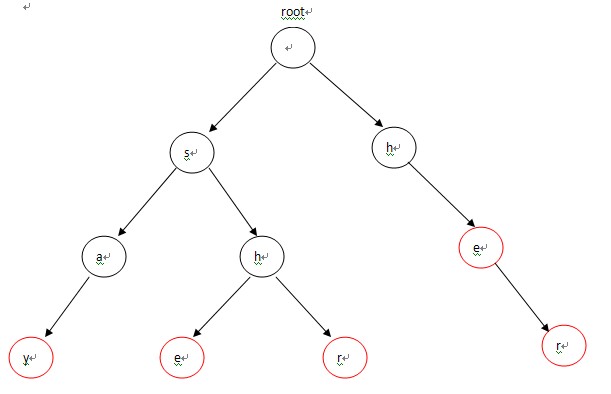
二、构造失败指针

用BFS来构造失败指针，与KMP算法相似的思想。

首先，root入队，第1次循环时处理与root相连的字符，也就是各个单词的第一个字符h和s，因为第一个字符不匹配需要重新匹配，所以第一个字符都指向root（root是Trie入口，没有实际含义）失败指针的指向对应下图中的(1)，(2)两条虚线；第2次进入循环后，从队列中先弹出h，接下来p指向h节点的fail指针指向的节点，也就是root；p=p->fail也就是p=NULL说明匹配序列为空，则把节点e的fail指针指向root表示没有匹配序列，对应图-2中的(3)，然后节点e进入队列；第3次循环时，弹出的第一个节点a的操作与上一步操作的节点e相同，把a的fail指针指向root，对应图-2中的(4)，并入队；第4次进入循环时，弹出节点h(图中左边那个)，这时操作略有不同。由于p->next[i]!=NULL(root有h这个儿子节点，图中右边那个)，这样便把左边那个h节点的失败指针指向右边那个root的儿子节点h，对应图-2中的(5)，然后h入队。以此类推：在循环结束后，所有的失败指针就是下图中的这种形式。

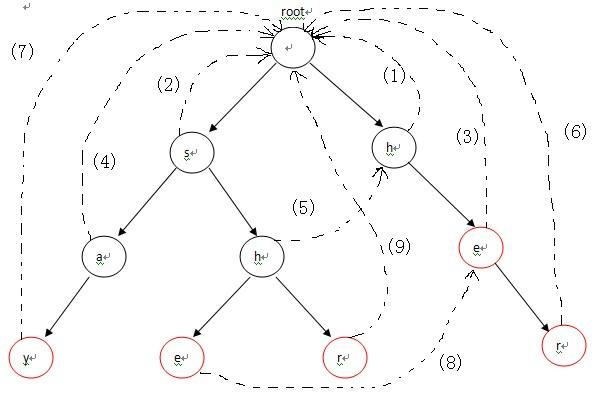
三、扫描

构造好Trie和失败指针后，我们就可以对主串进行扫描了。这个过程和KMP算法很类似，但是也有一定的区别，主要是因为AC自动机处理的是多串模式，需要防止遗漏某个单词，所以引入temp指针。

匹配过程分两种情况：(1)当前字符匹配，表示从当前节点沿着树边有一条路径可以到达目标字符，此时只需沿该路径走向下一个节点继续匹配即可，目标字符串指针移向下个字符继续匹配；(2)当前字符不匹配，则去当前节点失败指针所指向的字符继续匹配，匹配过程随着指针指向root结束。重复这2个过程中的任意一个，直到模式串走到结尾为止。

 对照上图，看一下模式匹配这个详细的流程，其中模式串为yasherhs。对于i=0,1。Trie中没有对应的路径，故不做任何操作；i=2,3,4时，指针p走到左下节点e。因为节点e的count信息为1，所以cnt+1，并且讲节点e的count值设置为-1，表示改单词已经出现过了，防止重复计数，最后temp指向e节点的失败指针所指向的节点继续查找，以此类推，最后temp指向root，退出while循环，这个过程中count增加了2。表示找到了2个单词she和he。当i=5时，程序进入第5行，p指向其失败指针的节点，也就是右边那个e节点，随后在第6行指向r节点，r节点的count值为1，从而count+1，循环直到temp指向root为止。最后i=6,7时，找不到任何匹配，匹配过程结束。

 

三、小试牛刀

题目：hdu2222 Keywords Search

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e7 + 5;
const int MAX = 10000000;
int cnt;
struct node{
    node *next[26];
    node *fail;
    int sum;
};
node *root;
char key[70];
node *q[MAX];
int head,tail;
node *newnode;
char pattern[maxn];
int N;
void Insert(char *s)
{
    node *p = root;
    for(int i = 0; s[i]; i++)
    {
        int x = s[i] - \'a\';
        if(p->next[x] == NULL)
        {
            newnode=(struct node *)malloc(sizeof(struct node));
            for(int j=0;j<26;j++) newnode->next[j] = 0;
            newnode->sum = 0;newnode->fail = 0;
            p->next[x]=newnode;
        }
        p = p->next[x];
    }
    p->sum++;
}
void build_fail_pointer()
{
    head = 0;
    tail = 1;
    q[head] = root;
    node *p;
    node *temp;
    while(head < tail)
    {
        temp = q[head++];
        for(int i = 0; i <= 25; i++)
        {
            if(temp->next[i])
            {
                if(temp == root)
                {
                    temp->next[i]->fail = root;
                }
                else
                {
                    p = temp->fail;
                    while(p)
                    {
                        if(p->next[i])
                        {
                            temp->next[i]->fail = p->next[i];
                            break;
                        }
                        p = p->fail;
                    }
                    if(p == NULL) temp->next[i]->fail = root;
                }
                q[tail++] = temp->next[i];
            }
        }
    }
}
void ac_automation(char *ch)
{
    node *p = root;
    int len = strlen(ch);
    for(int i = 0; i < len; i++)
    {
        int x = ch[i] - \'a\';
        while(!p->next[x] && p != root) p = p->fail;
        p = p->next[x];
        if(!p) p = root;
        node *temp = p;
        while(temp != root)
        {
           if(temp->sum >= 0)
           {
               cnt += temp->sum;
               temp->sum = -1;
           }
           else break;
           temp = temp->fail;
        }
    }
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        root=(struct node *)malloc(sizeof(struct node));
        for(int j=0;j<26;j++) root->next[j] = 0;
        root->fail = 0;
        root->sum = 0;
        scanf("%d",&N);
        getchar();
        for(int i = 1; i <= N; i++)
        {
            gets(key);
            Insert(key);
        }
        gets(pattern);
        cnt = 0;
        build_fail_pointer();
        ac_automation(pattern);
        printf("%d\\n",cnt);
    }
    return 0;
}