[提升性选讲] 树形DP进阶:一类非线性的树形DP问题(例题 BZOJ4403 BZOJ3167)

Posted 2020-10-02 LadyLex

转载请注明原文地址:http://www.cnblogs.com/LadyLex/p/7337179.html 

树形DP是一种在树上进行的DP相对比较难的DP题型.由于状态的定义多种多样,因此解法也五花八门,经常成为高水平考试的考点之一.

在树形DP的问题中，有这样一类问题：其数据范围相对较小，并且状态转移一般与两两节点之间的某些关系有关。

今天，我们就来研究一下这类型的问题，并且总结一种（相对套路的）解决大多数类型题的思路。

首先，我们用一道相对简单的例题来初步了解这个类型题的大致思路，以及一些基本的代码实现。

BZOJ 4033: [HAOI2015]树上染色

Time Limit: 10 Sec  Memory Limit: 256 MB

Description

有一棵点数为N的树，树边有边权。给你一个在0~N之内的正整数K，你要在这棵树中选择K个点，将其染成黑色，并

将其他的N-K个点染成白色。将所有点染色后，你会获得黑点两两之间的距离加上白点两两之间距离的和的收益。

问收益最大值是多少。

Input

第一行两个整数N,K。

接下来N-1行每行三个正整数fr,to,dis，表示该树中存在一条长度为dis的边(fr,to)。

输入保证所有点之间是联通的。

N<=2000,0<=K<=N

Output

输出一个正整数，表示收益的最大值。

Sample Input

5 2
1 2 3
1 5 1
2 3 1
2 4 2

Sample Output

17
【样例解释】
将点1,2染黑就能获得最大收益。

 

 

看完这道题，你有什么想法？一头雾水？

接下来，我们还是按照状态确立，状态转移，代码实习三个步骤来分析这道题，并且得出一些适用性的规律。

状态确立

　　首先,我们可以一眼看出,只用诸如"处理完以i为根的子树的最大收益"等一维的状态不能处理这个问题,

　　这个时候,我们可以考虑加一维来表示更多的限制条件:设f[i][j]表示"在以i为根的子树中染j个黑色点的最大收益",最终答案即是f[1][k]

状态转移

　　其实状态定义蛮好想,但是,怎么状态转移呢?

　　由于......数据范围很小,而我们权值的计算又与两两点之间关系有关,因此我们可以考虑枚举点对的暴力做法.

　　我们考虑,对于每个点对来说,他们之间的贡献只会在他们的LCA处贡献O(1)的时间复杂度.

　　由于一共只有n²数量级的点对,因此我们如果这样做的话算法复杂度是O(n²)的.

　　既然这种算法的复杂度是O(n²)的,我们就可以随便转移考虑一种暴力的转移:

　　枚举当前考虑的子树中有几个黑点,并考虑合并子树带来的贡献.

　　我们考虑,如果我们只统计当前子树内的贡献,显然是不好转移的,因为无法考虑与子树外面点的关系

　　所以,我们把子树外面的点与子树内点的贡献也统计在f数组里面,也就是说"外面伸进来的边"也被统计了进来

　　这样,由于子树内可以被统计的边的贡献已经被全部统计完,我们就可以通过考虑当前合并的两节点之间的这条边来统计贡献:

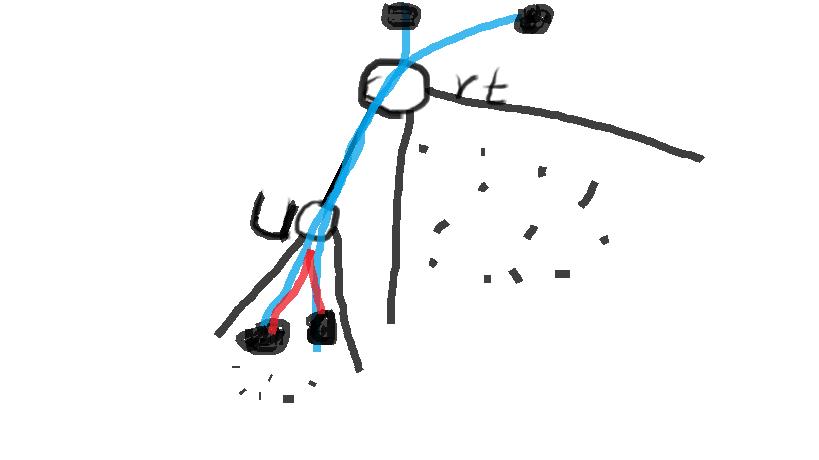
　　在上图中,子树里面红色边的贡献以及考虑完,现在我们更新的是子树外面的点与子树内的点通过蓝色边贡献的权值.

　　设节点rt的子树大小为size[rt],rt原来染色了j个黑点,设节点u的子树大小为size[u],u原来染色了v个黑点,设边权为val

　　经过图中的蓝边这条边,u里边的黑点与外面的黑点产生了v*(k-v)个黑点对.

　　同理,里边的白点与外面的白点产生了(size[u]-v])*(n-k-(size[u]-v))个白点对

　　那么rt->u这条边总共产生了(v*(k-v)+(size[u]-v])*(n-k-(size[u]-v)))*val的新的贡献.

　　这样我们就统计出来了新的贡献,现在以rt为根的子树总贡献是f[rt][j]+f[u][v]+(v*(k-v)+(size[u]-v])*(n-k-(size[u]-v)))*val

　　我们用上面这个式子去更新f[rt][j+v]的答案即可.

代码实现

 　　在代码中,这个算法是O(n²)就变得显而易见了.先给出dp过程的代码,我们开始分析:

 1 void dp(int rt,int fa)
 2 {
 3     register int i,j,k,u;
 4     LL cnt;size[rt]=1;
 5     for(i=adj[rt];i;i=s[i].next)
 6     {
 7         u=s[i].zhong;
 8         if(u!=fa)
 9         {
10             dp(u,rt);
11             memset(g,0,sizeof(g));
12             for(j=0;j<=size[rt];++j)
13                 for(k=0;k<=size[u];++k)
14                     cnt=k*1ll*(m-k)+(size[u]-k)*1ll*(n-m-(size[u]-k)),
15                     g[j+k]=max(g[j+k],f[rt][j]+f[u][k]+cnt*s[i].val);
16             size[rt]+=size[u];
17             for(j=0;j<=size[rt];++j)f[rt][j]=g[j];
18         }
19     }
20 }

　　就像上面说的,我们考虑把u这棵子树合并到rt里面产生的新贡献.

　　值得注意的一点是,我们如果先不合并起来,用刷表法去更新,要比先合并起来用填表法更新快不少.

　　这一点带来的优化很明显,因为合并后j循环的次数变多了.

　　具体的效率差别...大概是这样(上面那个提交是后合并的打法):

　　

　　现在,这道题基本就我们解决了.完整代码见下:

 1 #include <cstdio>
 2 #include <cstring>
 3 #include <algorithm>
 4 using namespace std;
 5 typedef long long LL;
 6 const int N=2010;
 7 int n,m,e,adj[N],size[N];
 8 LL f[N][N],g[N];
 9 struct edge{int zhong,next;LL val;}s[N<<1];
10 inline void add(int qi,int zhong,LL val)
11     {s[++e].zhong=zhong,s[e].val=val,s[e].next=adj[qi],adj[qi]=e;}
12 void dp(int rt,int fa)
13 {
14     register int i,j,k,u;
15     LL cnt;size[rt]=1;
16     for(i=adj[rt];i;i=s[i].next)
17     {
18         u=s[i].zhong;
19         if(u!=fa)
20         {
21             dp(u,rt);
22             memset(g,0,sizeof(g));
23             for(j=0;j<=size[rt];++j)
24                 for(k=0;k<=size[u];++k)
25                     cnt=k*1ll*(m-k)+(size[u]-k)*1ll*(n-m-(size[u]-k)),
26                     g[j+k]=max(g[j+k],f[rt][j]+f[u][k]+cnt*s[i].val);
27             size[rt]+=size[u];
28             for(j=0;j<=size[rt];++j)f[rt][j]=g[j];
29         }
30     }
31 }
32 int main()
33 {
34     scanf("%d%d",&n,&m);
35     register int i,a,b;LL c;
36     for(i=1;i<n;++i)
37         scanf("%d%d%lld",&a,&b,&c),add(a,b,c),add(b,a,c);
38     dp(1,0),printf("%lld\\n",f[1][m]);
39 }

 

 上面这道题还算一道比较简单的树形DP.这道题最大的特点就是那个非线性的O(n²)过程了.

这类非线性的DP一般状态定义和状态转移都比较复杂,但是主要的思想要点是"合并".

如果你发现某个树归问题是与两点间关系有关,那他很可能就是一个这种类型的DP

 下面,我们再来看一道题.这道题可就没有上题那么简单了...... 

BZOJ 3167: [Heoi2013]Sao

Time Limit: 30 Sec  Memory Limit: 256 MB

Description

Welcome to SAO(Strange and Abnormal Online)。这是一个VRMMORPG，含有n个关卡。但是，挑战不同关卡的顺序是一

个很大的问题。有n–1个对于挑战关卡的限制，诸如第i个关卡必须在第j个关卡前挑战，或者完成了第k个关卡才

能挑战第l个关卡。并且，如果不考虑限制的方向性，那么在这n–1个限制的情况下，任何两个关卡都存在某种程

度的关联性。即，我们不能把所有关卡分成两个非空且不相交的子集，使得这两个子集之间没有任何限制。

Input

第一行，一个整数T，表示数据组数。对于每组数据，第一行一个整数n，表示关卡数。接下来n–1行，每行为“i 

sign j”，其中0≤i,j≤n–1且i≠j，sign为“<”或者“>”，表示第i个关卡必须在第j个关卡前/后完成。

T≤5，1≤n≤1000

Output

对于每个数据，输出一行一个整数，为攻克关卡的顺序方案个数，mod1,000,000,007输出。

Sample Input

5
10
5 > 8
5 > 6
0 < 1
9 < 4
2 > 5
5 < 9
8 < 1
9 > 3
1 < 7
10
6 > 7
2 > 0
9 < 0
5 > 9
7 > 0
0 > 3
7 < 8
1 < 2
0 < 4
10
2 < 0
1 > 4
0 > 5
9 < 0
9 > 3
1 < 2
4 > 6
9 < 8
7 > 1
10
0 > 9
5 > 6
3 > 6
8 < 7
8 > 4
0 > 6
8 > 5
8 < 2
1 > 8
10
8 < 3
8 < 4
1 > 3
1 < 9
3 < 7
2 < 8
5 > 2
5 < 6
0 < 9

Sample Output

2580
3960
1834
5208
3336

 

首先,我们可以看出,原题等价于给树上的每个点分配一个权值，并使其满足一些大于&小于关系;

同样,一维的状态无法满足题目的要求.

为了方便处理,我们还是把原图当做一棵树处理.我们可以发现,一个点的子树中有比他大的,也有比他小的.

那么我们不妨再开一维来表示这种限制:设f[i][j]表示在以i为根的子树中有j个比i小的数.

那么状态有了,我们怎么转移呢?

我们可以发现,访问方案的不同与每对点的访问先后顺序有关.因此,我们可以考虑每一对点给最终方案带来的不同影响,

那么在转移的时候依然采用合并子树的思路,假设我们当前要合并rt的子树u,

以rt要求比u大为例:

我们设合并前以rt为根的子树中有i个比rt小,以u为根的子树中有j个比rt小

首先,原来的合法排列就有f[rt][i]种.又由于u比rt小,因此在刚才那j个比rt小的数中有几个比u小是不确定的,每一种方案都有可能出现,因此我们还需要乘上Σf[u][j],j∈[0,j]

接着,这j个比rt小的数插入的位置是不确定的,因此他们所处的位置不同会带来C(i+j)(j)的贡献种数.

同理,剩下size[u]-j个比rt大的数也会带来C(size[rt]+size[u]-i-j-1)(size[u]-j)这么多的贡献.

 

那么最终我们要更新的数量就是f[rt][i]*(Σf[u][j],j∈[0,j])*C(i+j)(j)*C(size[rt]+size[u]-i-j-1)(size[u]-j)

如果rt比u小那么同理,只不过我们枚举的方式变一下,看有几个数比rt大

如果我们处理f数组的前缀和的话,就可以做到O(n²)的转移啦!

代码见下:

 1 #include <cstdio>
 2 #include <cstring>
 3 #include <algorithm>
 4 using namespace std;
 5 typedef long long LL;
 6 const int mod=1000000007,N=1010;
 7 int n,adj[N],e;
 8 LL g[N],C[N][N],sum[N][N],size[N],f[N][N];//以i为根的子树，有j个比i小(在i之前访问)的方案数
 9 struct edge{int zhong,next,val;}s[N<<1];
10 inline void add(int qi,int zhong,int val)
11     {s[++e].zhong=zhong;s[e].val=val;s[e].next=adj[qi];adj[qi]=e;}
12 void dfs(int rt,int fa)
13 {
14     size[rt]=f[rt][0]=1;
15     for(int i=adj[rt];i;i=s[i].next)
16     {
17         int u=s[i].zhong;
18         if(u!=fa)
19         {
20             dfs(u,rt);int limit=size[rt]+size[u];
21             for(int i=0;i<limit;i++)g[i]=0;
22             if(s[i].val==1)//rt比u小
23                 for(int j=0;j<size[rt];j++)//已经合并完成的以rt为根节点的子树中有j个比rt大(在rt之前访问)
24                     for(int k=0;k<=size[u];k++)//以u为根节点的子树中有k个比rt大(在rt之后访问)
25                     {
26                         LL tmp1=f[rt][size[rt]-j-1]/*比rt小的size[rt]-j-1的合法方案数*/%mod*(sum[u][size[u]-1]-sum[u][size[u]-k-1]+mod)%mod;
27                             //u里面有k个比rt大的,不一定有几个比u大
28                         LL tmp2=C[j+k][k]*C[limit-j-k-1][size[u]-k]%mod;
29                                //组合数看方案数,前者表示在新的j+k个比rt大的数中新插入的k个数所在的位置
30                             //后者表示比rt小的size-j-k-1个数中u剩下的size[u]-k的排列
31                         g[limit-j-k-1]=(g[limit-j-k-1]+tmp1*tmp2%mod)%mod;
32                         //此时有limit-j-k-1个数比rt小,更新答案
33                     }
34             else//rt比u大(在u之后访问)
35                 for(int j=0;j<size[rt];j++)//以rt为根节点的子树中有j个比rt小
36                     for(int k=0;k<=size[u];k++)//以u为根节点的子树中有k个比rt小
37                     {
38                         LL tmp1=f[rt][j]%mod*sum[u][k-1]%mod;
39                             //u里面有k个比rt小的,不一定几个比u小
40                         LL tmp2=C[j+k][k]*C[limit-j-k-1][size[u]-k]%mod;//和上面组合数的统计类似.
41                         g[j+k]=(g[j+k]+tmp1*tmp2%mod)%mod;
42                     }
43             size[rt]+=size[u];//不断合并每棵子树
44             for(int j=0;j<size[rt];j++)f[rt][j]=g[j];//更新f数组
45         }
46     }
47     sum[rt][0]=f[rt][0];
48     for(int j=1;j<size[rt];j++)sum[rt][j]=(sum[rt][j-1]+f[rt][j])%mod;//全部合并完成,计算合法方案前缀和
49 }
50 int main()
51 {
52     for(int i=0;i<=1000;i++)
53     {
54         C[i][0]=1;
55         for(int j=1;j<=i;j++)
56             C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
57     }
58     int t,a,b;char c[3];scanf("%d",&t);
59     while(t--)
60     {
61         scanf("%d",&n);
62         memset(size,0,sizeof(size));
63         memset(f,0,sizeof(f));
64         memset(sum,0,sizeof(sum));
65         e=0;memset(adj,0,sizeof(adj));
66         for(int i=1;i<n;i++)
67         {
68             scanf("%d%s%d",&a,c,&b),a++,b++;
69             if(c[0]==\'>\')add(b,a,1),add(a,b,-1);
70             else add(a,b,1),add(b,a,-1);
71         }
72         dfs(1,0);int ans=0;
73         for(int i=0;i<n;i++)
74             ans=(ans+f[1][i])%mod;
75         printf("%d\\n",ans);
76     }
77 }

非线性的树形DP是一类很考验DP思维,尤其是DP状态定义能力的问题,这就需要OIer们通过刷题来不断积累做题经验了(其实什么类型题不是呢).希望大家能从我的博文中有所收获:)