[入门向选讲] 插头DP:从零概念到入门 (例题:HDU1693 COGS1283 BZOJ2310 BZOJ2331)
Posted LadyLex
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[入门向选讲] 插头DP:从零概念到入门 (例题:HDU1693 COGS1283 BZOJ2310 BZOJ2331)相关的知识,希望对你有一定的参考价值。
转载请注明原文地址:http://www.cnblogs.com/LadyLex/p/7326874.html
最近搞了一下插头DP的基础知识……这真的是一种很锻炼人的题型……
每一道题的状态都不一样,并且有不少的分类讨论,让插头DP十分锻炼思维的全面性和严谨性。
下面我们一起来学习插头DP的内容吧!
插头DP主要用来处理一系列基于连通性状态压缩的动态规划问题,处理的具体问题有很多种,并且一般数据规模较小。
由于棋盘有很特殊的结构,使得它可以与“连通性”有很强的联系,因此插头DP最常见的应用要数在棋盘模型上的应用了。
下面我们给出一道很简单的例题,并且由这道简单的例题构建出插头DP的基本解题思路,在状态确立,状态转移以及程序实现几个方面进行一一介绍.
例题一:HDU1693 Eat the Trees
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
So Pudge’s teammates give him a new assignment—Eat the Trees!
The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.
Now Pudge has a question, how many ways are there to eat the trees?
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))

For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.
状态确立
首先,我们要了解插头DP中最重要的关键词:“插头”
---插头
在插头DP中,插头表示一种联通的状态,以棋盘为例,一个格子有一个向某方向的插头,就意味着这个格子在这个方向可以与外面相连(与插头那边的格子联通)。
值得注意的一点是,插头不是表示将要去某处的虚拟状态,而是表示已经到达某处的现实状态。
也就是说,如果有一个插头指向某个格子,那么这个格子已经和插头来源联通了,我们接下来要考虑的是从这个插头往哪里走。
这是很重要的一点理解,下面讨论的状态转移都是在此基础上展开的,请务必注意。
我们已经有了插头,自然要利用插头来状态转移。一般来说,我们从上往下,从左往右逐行逐格递推。
---逐格递推
我们考虑第i行的某一个格子:走向它的方案,可能由上一行的下插头转移而来,也可能是本行的右插头转移而来。
因此我们需要记录这些地方有没有插头,也就是利用状压的思想。我们记录的这个“有没有插头”的东西,就被我们称为轮廓线。字面意思,轮廓线就是记录了棋盘这一行与上一行交界的轮廓中插头的情况。轮廓线上方是已经决策完的格子,下方是未决策的。显然,对于本题的轮廓线,与它直接相连的格子有m个,插头有m+1个,我个人的习惯是给插头编号0~m。

·上图就是轮廓线的一种可能情况。
由于数据范围比较小,轮廓线的插头状态我们一般可以利用X进制压位来表示。
对于本题来说,题目的限制条件比较少,可以走多个回路,而不是像某些题一样只能走一个回路(走一个回路的时候要维护插头间的连通性,我们下文再讨论),因此我们直接记录,只要用二进制来表示某一位置有没有插头即可:设0表示没有插头,1表示有插头。(大概这是最简单的一种插头类型了......)
状态转移
---行间转移
我们先考虑两行之间的转移:显然,第i行的下插头决定了第i+1行的格子有没有上插头,因此我们应该把这个信息传递到下一行。
在转移的时候,当前行插头0到插头m-1可能会给下一行带来贡献,而第m个插头一定为0(结合定义,想一下为什么)。
容易发现,当前行的0~m-1号插头会变成下一行初始的1~m号插头,因此我们可以直接利用位运算进行转移。
对于本题,只需要将上一行的某个状态左移一位(<<1,即*2)即可
行间的转移还是比较简单的,具体代码实现的话,下面是一种可以参考的方式
(这是我刚学插头DP时候用的一种比较蠢的打法,使用状态数组f[i][j][k]表示决策到第i行第j列,插头状态为k的方案数,后面使用Hash表的时候我们还有其他方式)
1 if(i<n)//bin[i]表示2的i次方 2 for(int j=0;j<bin[m];j++) 3 f[i+1][0][j<<1]=f[i][m][j];
下面我们考虑具体的逐格转移,这也是插头DP的核心模块所在。
对于本题来说,当我们决策到某个格子(x,y)时,假如它不是障碍格子,可能会出现如下三种情况:

情况1,这个格子没有上插头,也没有左插头,那么由于我们要遍历整张图,所以我们要新建插头,把这个格子与其他格子连起来,相应的,我们要把原来轮廓线对应位置的插头改为1.
情况2,这个位置有上插头,也有左插头。由于我们不要求只有一条回路,因此回路可以在这里结束。我们直接更新答案即可。
情况3,只有一个插头。那么这个插头可以向其他方向走:向下和向右均可以。所以我们修改一下轮廓线并更新对应状态的答案即可。
值得注意的是,如果一个格子是障碍格,那么当且仅当没有插头连向它时,这才是一个合法状态。因为根据我们刚才插头的定义:
“值得注意的一点是,插头不是表示将要去某处的虚拟状态,而是表示已经到达某处的现实状态。
也就是说,如果有一个插头指向某个格子,那么这个格子已经和插头来源联通了,我们接下来要考虑的是从这个插头往哪里走。”
所以,对应障碍格既不能连入插头,也不能连出插头。这一点需要特别注意。
代码实现
本题的分类讨论还是相对简单的,在处理完上面的内容后我们只需要按照上面的思路代码实现即可。
(代码里状态转移很有意思……)
1 #include <cstdio> 2 #include <cstring> 3 using namespace std; 4 typedef long long LL; 5 int n,m,bin[20],mp[13][13]; 6 LL f[13][13][(1<<12)+10]; 7 inline void Execution(int x,int y) 8 { 9 int plug1=bin[y-1],plug2=bin[y]; 10 for(int j=0;j<bin[m+1];j++) 11 if(mp[x][y]) 12 { 13 f[x][y][j]+=f[x][y-1][j^plug1^plug2]; 14 if( (( j>>(y-1) )&1)== ((j>>(y) )&1) )continue; 15 f[x][y][j]+=f[x][y-1][j]; 16 } 17 else 18 if(!(j&plug1)&&!(j&plug2))f[x][y][j]=f[x][y-1][j]; 19 else f[x][y][j]=0; 20 } 21 int main() 22 { 23 int t;scanf("%d",&t); 24 bin[0]=1;for(int i=1;i<=15;i++)bin[i]=bin[i-1]<<1; 25 for(int u=1;u<=t;u++) 26 { 27 scanf("%d%d",&n,&m); 28 for(int i=1;i<=n;i++) 29 for(int j=1;j<=m;j++) 30 scanf("%d",&mp[i][j]); 31 memset(f,0,sizeof(f));f[1][0][0]=1; 32 for(int i=1;i<=n;i++) 33 { 34 for(int j=1;j<=m;j++)Execution(i,j); 35 if(i!=n)for(int j=0;j<bin[m];j++) 36 f[i+1][0][j<<1]=f[i][m][j]; 37 } 38 printf("Case %d: There are %lld ways to eat the trees.\\n",u,f[n][m][0]); 39 } 40 }
通过刚才这道题,你应该已经对插头DP是什么,以及插头DP的基本概念与思想有了基本的了解。
那么下面,我们通过下一道题来强化分类讨论能力,以及学习对连通性的限制方法。
例题2:COGS1283. [HNOI2004] 邮递员
时间限制:10 s 内存限制:162 MB
【题目描述】
Smith在P市的邮政局工作,他每天的工作是从邮局出发,到自己所管辖的所有邮筒取信件,然后带回邮局。
他所管辖的邮筒非常巧地排成了一个m*n的点阵(点阵中的间距都是相等的)。左上角的邮筒恰好在邮局的门口。
Smith是一个非常标新立异的人,他希望每天都能走不同的路线,但是同时,他又不希望路线的长度增加,他想知道他有多少条不同的路线可走。
你的程序需要根据给定的输入,给出符合题意的输出:
l 输入包括点阵的m和n的值;
l 你需要根据给出的输入,计算出Smith可选的不同路线的总条数;
【输入格式】
输入文件postman.in只有一行。包括两个整数m, n(1 <= m <= 10, 1 <= n <= 20),表示了Smith管辖内的邮筒排成的点阵。
【输出格式】
输出文件只有一行,只有一个整数,表示Smith可选的不同路线的条数。
【样例输入】
2 2 说明:该输入表示,Smith管辖了2*2的一个邮筒点阵。
【样例输出】
2
【提示】
有了上一题的经验,不难看出,本题依然是一个在棋盘模型上解决的简单回路问题(简单回路是指起点和终点相同的简单路径)。
而我们要求的是能一遍遍历整个棋盘的简单回路个数。
可是,如果直接搬用上一题的做法,你会发现一些问题:
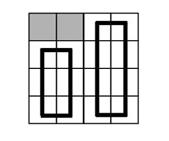
比如对于上图的情况,在上一题中这是一个合法解,但在本题中不是。那么我们就应该思考上题插头定义的片面性在哪里,并想出新的插头定义。
容易观察到,如果每个格子都在回路中的话,最后所有的格子应该都通过插头连接成了一个连通块。
因此我们还需要记录每行格子的连通情况.这时我们就要引入一种新的方法:最小表示法。这是一种用来标记连通性的方法。
具体的过程是:第一个非障碍格子以及与它连通的所有格子标记为1,然后再找第一个未标记的非障碍格子以及与它连通的格子标记为2,……重复这个过程,直到所有的格子都标记完毕.比如连通信息((1,2,5),(3,6),(4)),就可以表示为{1,1,2,3,1,2}
但是,在实际的代码实现中,这样的最小表示法有些冗余:如果某个格子没有下插头,那么它就不会对下一行的格子产生影响,这个状态就是多余的。
因此,我们转换优化的角度,用最小表示法来表示插头的联通性:如果这个插头存在,那么就标记这个插头对应的格子的连通标号,如果这个插头不存在,那么标记为0..
在这样优化后,不仅状态表示更加简单,而且状态总数将会大大减少.
接下来,我们用改进过的最小表示法,继续思考上面的问题:如何定义新的插头状态?
如果每个格子都在回路中的话,我们还可以得到,每个格子应该恰好有且仅有2个插头。
我们来看下面几张图片:
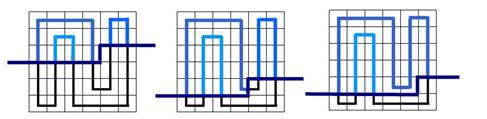
相信细心的你能够发现,轮廓线上方的路径是由若干条互不相交的路径构成的(这是肯定的,简单反证:如果最终相交就构不成回路了)。
更有趣的是,每条路径的两个端点恰好对应了轮廓线上的两个插头。
我们又知道,一条路径应该对应着一个连通块,因此这两个插头同属一个连通块,并且不与其他的连通块联通
并且,我们在状态转移的时候也不会改变这种性质:
上文的情况1对应着新增一条路径,插头为2;
情况2意味着把2条路径合为一条,联通块变为1个,插头还是2个;
情况3只有一个插头压根不会改变插头数量。
那么现在我们知道了,简单回路问题一定满足任何时候轮廓线上每一个连通分量恰好有2个插头。
互不相交……两个插头……展开你的联想,你能想到什么?
没错,这正是括号匹配!我们可以按照与括号匹配相似的方式,将轮廓线上每一条路径上中左边那个插头标记为左括号插头,右边那个插头标记为右括号插头。
由于插头之间不会交叉,那么左括号插头一定可以与右括号插头一一对应。
这样我们就可以解决上面的联通性问题:我们可以使用一种新的定义方式:3进制表示——0表示无插头,1表示左括号插头,2表示右括号插头,记录下所有的轮廓线信息。
但是,值得注意的是,X进制的解码转码是较慢而且较麻烦的。
在空间允许的情况下,建议使用2k进制,并且加上Hash表去重。这样不仅可以减少状态,由于仍然可以使用二进制位运算,运算速度相比之下也增加了不少。
下面,我们利用刚才新的插头定义方式来考虑本题的状态转移问题。
依然设当前转移到格子(x,y),设y-1号插头状态为p1,y号插头状态为p2。
情况1:p1==0&&p2==0.
这种状态和上一题的情况1是类似的,我们只需要新建一个新路径即可:下插头设为左括号插头,右插头设为右括号插头
情况2:p1==0&&p2!=0.
这种状态和上一题的状态3类似,我们依然可以选择“直走”和“转弯”两种策略
情况3:p1!=0&&p2==0.
这种状态和情况2类似,不再赘述。
情况4:p1==1&&p2==1.
这种状态把2个左括号插头相连,那么我们需要将右边那个左括号插头(p2)对应的右括号插头q2修改成左括号插头。
情况5:p1==1&&p2==2.
由于路径两两不相交,所以这种情况只能是自己和自己撞在了一起,即形成了回路。
由于只能有一条回路,因此只有在x==n&&y==m时,这种状态才是合法的,我们可以用它更新答案。



情况6:p1==2&&p2==1.
这种状态相当于把2条路径相连,并没有更改其他的插头
情况7:p1==2&&p2==2.
这种状态与情况4相似,这种状态把2个右括号插头相连,那么我们需要将左边那个右括号插头(p1)对应的左括号插头q1修改成右括号插头。
接下来我们只要代码实现上述过程即可。
但我们依然有一个很大的优化点:Hash表的使用。Hash表可以通过去重以及排除无用状态极大的加速插头DP的速度。
Hash表的打法不唯一,下面仅介绍我学习的打法(感谢stdafx学长)
与Hash表相关的主要内容有:
1.mod变量,为Hash表的大小和模数
2.size变量,存储Hash表大小;
3.hash数组,存储某个余数对应的编号
4.key数组,存储状态
5.val数组,存某个状态对应的方案数
在给出一个新状态时,我们在已有Hash表内搜索是否存在这一状态,如果有,那就修改这个状态对应的val值;如果没有,那就给他新建一个编号
具体的代码实现大概长这样:
1 struct node{int state,next;}; 2 struct Hash_map 3 { 4 int val[MOD],adj[MOD],e;node s[MOD]; 5 inline void intn() 6 { 7 memset(val,0x7f,sizeof(val)),e=0, 8 memset(s,0,sizeof(s)),memset(adj,0,sizeof(adj)); 9 } 10 inline int &operator [] (const int &State) 11 { 12 int pos=State%MOD,i; 13 for(i=adj[pos];i&&s[i].state!=State;i=s[i].next); 14 if(!i)s[++e].state=State,s[e].next=adj[pos],adj[pos]=i=e; 15 return val[i]; 16 } 17 }f[2];
有了Hash表,我们再来考虑状态转移时的几个小细节:
我们状态转移的主要工作一般有三个:
1.查询某个插头对应的类型(对应下文Find)
2.查找与某个插头匹配的对应插头(对应下文Link)
3.修改状态中某个插头的类型(对应下文Set)
由于这三个操作很常用,所以我把他们写成了函数,方便调用。这三个操作的代码见下:
1 inline int Find(int State,int id){return (State>>((id-1)<<1))&3;} 2 inline void Set(int &State,int bit,int val){bit=(bit-1)<<1;State|=3<<bit,State^=3<<bit,State|=val<<bit;} 3 inline int Link(int State,int pos) 4 { 5 int cnt=0,Delta=(Find(State,pos)==1)?1:-1;//这个变量决定向左寻找匹配还是向右 6 for(int i=pos;i&&i<=m+1;i+=Delta) 7 { 8 int plug=Find(State,i); 9 if(plug==1)cnt++; 10 else if(plug==2)cnt--; 11 if(cnt==0)return i; 12 } 13 return -1; 14 }
有了上面这些操作,本题的全部代码实现已经水到渠成了:我们只需要把上面7种情况一一对应实现即可。代码见下:
(还有一个注意点,记得写高精度!)
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <cmath> 5 using namespace std; 6 typedef long long LL; 7 const int cube=(int)1e9,mod=2601; 8 int n,m; 9 struct Data_Analysis 10 { 11 int bit[6]; 12 inline void Clear(){memset(bit,0,sizeof(bit));} 13 Data_Analysis(){Clear();} 14 inline void Set(int t){Clear();while(t)bit[++bit[0]]=t%cube,t/=cube;} 15 inline int &operator [](int x){return bit[x];} 16 inline void Print() 17 { 18 printf("%d",bit[bit[0]]); 19 for(int i=bit[0]-1;i>0;i--)printf("%09d",bit[i]); 20 printf("\\n"); 21 } 22 inline Data_Analysis operator + (Data_Analysis b) 23 { 24 Data_Analysis c;c.Clear(); 25 c[0]=max(bit[0],b[0])+1; 26 for(int i=1;i<=c[0];i++) 27 c[i]+=bit[i]+b[i],c[i+1]+=c[i]/cube,c[i]%=cube; 28 while(!c[c[0]])c[0]--; 29 return c; 30 } 31 inline void operator += (Data_Analysis b){*this=*this+b;} 32 inline void operator = (int x){Set(x);} 33 }Ans; 34 struct Hash_Sheet 35 { 36 Data_Analysis val[mod]; 37 int key[mod],size,hash[mod]; 38 inline void Initialize() 39 { 40 memset(val,0,sizeof(val)),memset(key,-1,sizeof(key)); 41 size=0,memset(hash,0,sizeof(hash)); 42 } 43 inline void Newhash(int id,int v){hash[id]=++size,key[size]=v;} 44 Data_Analysis &operator [](const int State) 45 { 46 for(int i=State%mod;;i=(i+1==mod)?0:i+1) 47 { 48 if(!hash[i])Newhash(i,State); 49 if(key[hash[i]]==State)return val[hash[i]]; 50 } 51 } 52 }f[2]; 53 inline int Find(int State,int id){return (State>>((id-1)<<1))&3;} 54 inline void Set(int &State,int bit,int val){bit=(bit-1)<<1;State|=3<<bit,State^=3<<bit,State|=val<<bit;} 55 inline int Link(int State,int pos) 56 { 57 int cnt=0,Delta=(Find(State,pos)==1)?1:-1; 58 for(int i=pos;i&&i<=m+1;i+=Delta) 59 { 60 int plug=Find(State,i); 61 if(plug==1)cnt++; 62 else if(plug==2)cnt--; 63 if(cnt==0)return i; 64 } 65 return -1; 66 } 67 inline void Execution(int x,int y) 68 { 69 int now=((x-1)*m+y)&1,last=now^1,tot=f[last].size; 70 f[now].Initialize(); 71 for(int i=1;i<=tot;i++) 72 { 73 int State=f[last].key[i]; 74 Data_Analysis Val=f[last].val[i]; 75 int plug1=Find(State,y),plug2=Find(State,y+1); 76 if(Link(State,y)==-1||Link(State,y+1)==-1)continue; 77 if(!plug1&&!plug2){if(x!=n&&y!=m)Set(State,y,1),Set(State,y+1,2),f[now][State]+=Val;} 78 else if(plug1&&!plug2) 79 { 80 if(x!=n)f[now][State]+=Val; 81 if(y!=m)Set(State,y,0),Set(State,y+1,plug1),f[now][State]+=Val; 82 } 83 else if(!plug1&&plug2) 84 { 85 if(y!=m)f[now][State]+=Val; 86 if(x!=n)Set(State,y,plug2),Set(State,y+1,0),f[now][State]+=Val; 87 } 88 else if(plug1==1&&plug2==1) 89 Set(State,Link(State,y+1),1),Set(State,y,0),Set(State,y+1,0),f[now][State]+=Val; 90 else if(plug1==1&&plug2==2){if(x==n&&y==m)Ans+=Val;} 91 else if(plug1==2&&plug2==1)Set(State,y,0),Set(State,y+1,0),f[now][State]+=Val; 92 else if(plug1==2&&plug2==2) 93 Set(State,Link(State,y),2),Set(State,y,0),Set(State,y+1,0),f[now][State]+=Val; 94 } 95 } 96 int main() 97 { 98 scanf("%d%d",&n,&m); 99 if(n==1||m==1){printf("1\\n");return 0;} 100 if(m>n)swap(n,m); 101 f[0].Initialize();f[0][0]=1; 102 for(int i=1;i<=n;i++) 103 { 104 for(int j=1;j<=m;j++)Execution(i,j); 105 if(i!=n) 106 { 107 int now=(i*m)&1,tot=f[now].size; 108 for(int j=1;j<=tot;j++) 109 f[now].key[j]<<=2; 110 } 111 } 112 Ans+=Ans;Ans.Print(); 113 }
通过这道题的历练,相信你对插头DP的插头定义,最小表示法,以及状态优化的方法有了一定的了解。
尤其需要培养的是插头定义的“手感”,插头定义绝对是你解题的关键。
接下来,我们把目光转移到“简单路径”上来。通过下面这道例题,相信会对这类简单路径&回路问题有更深的理解。
BZOJ 2310: ParkII
Time Limit: 20 Sec Memory Limit: 128 MBDescription
Hnoi2007-Day1有一道题目 Park:给你一个 m * n 的矩阵,每个矩阵内有个
权值V(i,j) (可能为负数),要求找一条回路,使得每个点最多经过一次,并且经过
的点权值之和最大,想必大家印象深刻吧.
无聊的小 C 同学把这个问题稍微改了一下:要求找一条路径,使得每个点
最多经过一次,并且点权值之和最大,如果你跟小 C 一样无聊,就麻烦做一下
这个题目吧.
Input
第一行 m, n,接下来 m行每行 n 个数即V( i,j)
Output
一个整数表示路径的最大权值之和.
Sample Input
1 -2 1
1 1 1
Sample Output
【数据范围】
30%的数据,n≤6;100%的数据,m<=100,n ≤ ≤8.
注意:路径上有可能只有一个点.
以上是关于[入门向选讲] 插头DP:从零概念到入门 (例题:HDU1693 COGS1283 BZOJ2310 BZOJ2331)的主要内容,如果未能解决你的问题,请参考以下文章
猴子课堂:插头DP(基于连通性状态压缩的动态规划问题)(让你从入门到绝望)