[POJ 2104]K-th Number
Posted NaVi_Awson
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[POJ 2104]K-th Number相关的知识,希望对你有一定的参考价值。
Description
You are working for Macrohard company in data structures department. After failing your previous task about key insertion you were asked to write a new data structure that would be able to return quickly k-th order statistics in the array segment.
That is, given an array a[1...n] of different integer numbers, your
program must answer a series of questions Q(i, j, k) in the form: "What
would be the k-th number in a[i...j] segment, if this segment was
sorted?"
For example, consider the array a = (1, 5, 2, 6, 3, 7, 4). Let the
question be Q(2, 5, 3). The segment a[2...5] is (5, 2, 6, 3). If we sort
this segment, we get (2, 3, 5, 6), the third number is 5, and therefore
the answer to the question is 5.
Input
The first line of the input file contains n --- the size of the array, and m --- the number of questions to answer (1 <= n <= 100 000, 1 <= m <= 5 000).
The second line contains n different integer numbers not exceeding 109 by their absolute values --- the array for which the answers should be given.
The following m lines contain question descriptions, each
description consists of three numbers: i, j, and k (1 <= i <= j
<= n, 1 <= k <= j - i + 1) and represents the question Q(i, j,
k).
Output
For each question output the answer to it --- the k-th number in sorted a[i...j] segment.
Sample Input
7 3
1 5 2 6 3 7 4
2 5 3
4 4 1
1 7 3
Sample Output
5
6
3
HINT
This problem has huge input,so please use c-style input(scanf,printf),or you may got time limit exceed.
题目大意
求不修改的区间$k$小值。
题解
这道题做法有很多,据说某种奇妙的暴力可以过,还有《挑战程序设计竞赛》上说的平方分割、分桶法等等可以做。这些就先不讨论。这里介绍$5$种常见的做法。
解法一 莫队(+离散化+树状数组+二分)
一看到题,区间求值,就想到万能的莫队。
我们将数值哈希一下,将值域范围缩小。
做莫队的同时维护一个树状数组,记录出现次数。 询问的时候可以考虑二分,在树状数组中查找第$k$小的数。

1 #include<map> 2 #include<set> 3 #include<ctime> 4 #include<cmath> 5 #include<queue> 6 #include<stack> 7 #include<cstdio> 8 #include<string> 9 #include<vector> 10 #include<cstdlib> 11 #include<cstring> 12 #include<iostream> 13 #include<algorithm> 14 #define LL long long 15 #define RE register 16 #define IL inline 17 #define lowbit(x) (x&-x) 18 using namespace std; 19 const int N=100000; 20 const int M=5000; 21 const int INF=2e9; 22 23 struct tt 24 { 25 int num,pos,id; 26 }a[N+5]; 27 int rem[N+5]; 28 int n,m,lim; 29 IL bool comp(tt a,tt b) {return a.num<b.num;} 30 IL bool accomp(tt a,tt b) {return a.pos<b.pos;} 31 32 struct ss 33 { 34 int l,r,k,id; 35 }q[M+5]; 36 IL bool qcomp(ss a,ss b) {return a.l/lim==b.l/lim ? a.r<b.r : a.l<b.l;} 37 38 int c[N+5]; 39 void Add(int a,int k) {for (;a<=n;a+=lowbit(a)) c[a]+=k;} 40 int Count(int a) 41 { 42 int sum=0; 43 for (;a;a-=lowbit(a)) sum+=c[a]; 44 return sum; 45 } 46 int Dev(int k) 47 { 48 int l=1,r=n,mid,ans; 49 while (l<=r) 50 { 51 mid=(l+r)>>1; 52 if (Count(mid)>=k) r=mid-1,ans=mid; 53 else l=mid+1; 54 } 55 return rem[ans]; 56 } 57 58 int ans[M+5]; 59 60 int main() 61 { 62 scanf("%d%d",&n,&m); 63 lim=sqrt(double(n)); 64 for (RE int i=1;i<=n;i++) scanf("%d",&a[i].num),a[i].pos=i; 65 sort(a+1,a+n+1,comp); 66 a[0].num=-INF; 67 for (RE int i=1;i<=n;i++) a[i].id=a[i-1].id+(a[i].num!=a[i-1].num),rem[a[i].id]=a[i].num; 68 sort(a+1,a+n+1,accomp); 69 for (RE int i=1;i<=m;i++) scanf("%d%d%d",&q[i].l,&q[i].r,&q[i].k),q[i].id=i; 70 sort(q+1,q+m+1,qcomp); 71 int curl=1,curr=0,l,r; 72 for (RE int i=1;i<=m;i++) 73 { 74 l=q[i].l,r=q[i].r; 75 while (curl<l) Add(a[curl++].id,-1); 76 while (curl>l) Add(a[--curl].id,1); 77 while (curr<r) Add(a[++curr].id,1); 78 while (curr>r) Add(a[curr--].id,-1); 79 ans[q[i].id]=Dev(q[i].k); 80 } 81 for (RE int i=1;i<=m;i++) printf("%d\\n",ans[i]); 82 return 0; 83 }
具体复杂度这里不给出分析,贴张图:

解法二 归并树(+二分)
构造一棵归并树。
询问的时候需要二分答案,再在归并树内找比二分出的值小的元素个数。

1 #include<map> 2 #include<set> 3 #include<ctime> 4 #include<cmath> 5 #include<queue> 6 #include<stack> 7 #include<cstdio> 8 #include<string> 9 #include<vector> 10 #include<cstdlib> 11 #include<cstring> 12 #include<iostream> 13 #include<algorithm> 14 #define LL long long 15 #define RE register 16 #define IL inline 17 using namespace std; 18 const int N=100000; 19 const int ST_SIZE=1<<18; 20 21 int n,m; 22 int a[N],c[N]; 23 vector<int>dat[ST_SIZE]; 24 25 void init(int k,int l,int r) 26 { 27 if (r-l==1) dat[k].push_back(a[l]); 28 else 29 { 30 int chl=2*k+1,chr=2*k+2; 31 int m=(l+r)>>1; 32 init(chl,l,m); 33 init(chr,m,r); 34 dat[k].resize(r-l); 35 merge(dat[chl].begin(),dat[chl].end(), 36 dat[chr].begin(),dat[chr].end(),dat[k].begin()); 37 } 38 } 39 40 int cnt(int a,int b,int k,int l,int r,int num) 41 { 42 if (a<=l&&r<=b) 43 return lower_bound(dat[k].begin(),dat[k].end(),num)-dat[k].begin(); 44 else if (l>=b||a>=r) return 0; 45 else 46 { 47 int chl=2*k+1,chr=2*k+2; 48 int m=(l+r)>>1; 49 int res=cnt(a,b,chl,l,m,num); 50 res+=cnt(a,b,chr,m,r,num); 51 return res; 52 } 53 } 54 55 int main() 56 { 57 scanf("%d%d", &n,&m); 58 for (RE int i=0;i<n;i++) 59 { 60 scanf("%d",&a[i]); 61 c[i]=a[i]; 62 } 63 sort(c,c+n); 64 init(0,0,n); 65 int x,y,k; 66 for (RE int i=0;i<m;i++) 67 { 68 scanf("%d%d%d",&x,&y,&k); 69 int lb=0,ub=n; 70 while (ub-lb>1) 71 { 72 int mid=(ub+lb)>>1; 73 int num=c[mid]; 74 if (cnt(x-1,y,0,0,n,num)<k) lb=mid; 75 else ub=mid; 76 } 77 printf("%d\\n",c[lb]); 78 } 79 return 0; 80 }
归并树跑得就比较慢了:

解法三 划分树
划分树是基于快速排序的,首先将原始数组$a[]$进行排序$sorted[]$,然后取中位数$m$,将未排序数组中小于$m$放在$m$左边,大于$m$的放在$m$右边,并记下原始数列中每个数左边有多少数小于$m$,用数组$num_.left[depth][]$表示,这就是建树过程。
重点在于查询过程,设$[L,R]$为要查询的区间,$[l,r]$为当前区间,$s$表示$[L,R]$有多少数放到左子树,$ss$表示$[l,L-1]$有多少数被放倒左子树,如果$s$大于等于$K$,也就是说第$K$大的数肯定在左子树里,下一步就查询左子树,但这之前先要更新$L$,$R$,新的$newl=l+ss$, $newr=newl+s-1$。如果$s$小于$k$,也就是说第$k$大的数在右子树里,下一步查询右子树,也要先更新$L$,$R$,$dd$表示$[l,L-1]$中有多少数被放到右子树,$d$表示$[L,R]$有多少数被放到右子树,那么$newl = m+1+dd$,$newr=m+d+dd$, 这样查询逐渐缩小查询区间,直到最后$L==R$ 返回最后结果就行。
给出一个大牛的图片例子,
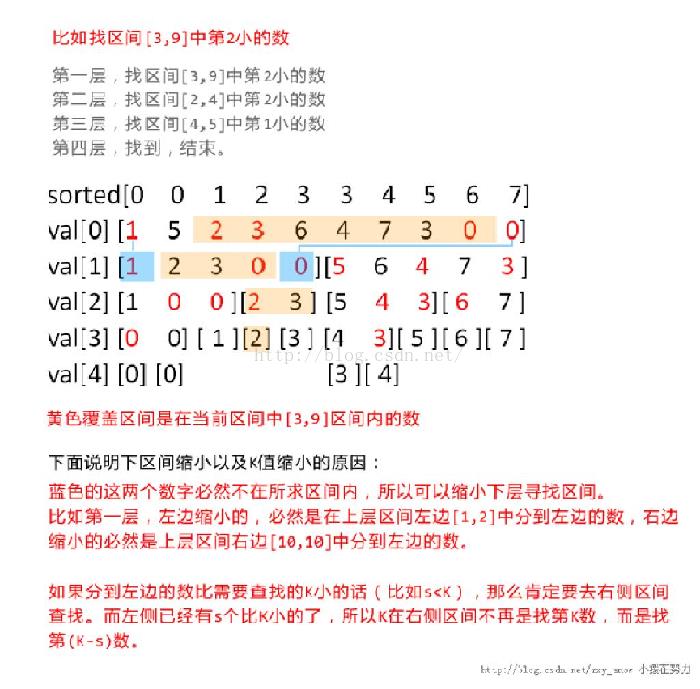
注意代码中的一些变量和题解不一致!

1 #include<map> 2 #include<set> 3 #include<ctime> 4 #include<cmath> 5 #include<queue> 6 #include<stack> 7 #include<cstdio> 8 #include<string> 9 #include<vector> 10 #include<cstdlib> 11 #include<cstring> 12 #include<iostream> 13 #include<algorithm> 14 #define LL long long 15 #define RE register 16 #define IL inline 17 using namespace std; 18 const int N=100000; 19 20 int n,m; 21 int sorted[N+5]; 22 int f[N+5][20]; 23 int num_left[N+5][20]; 24 25 void Build(int l,int r,int d) 26 { 27 if (l==r) return; 28 int mid=(l+r)>>1; 29 int lsame=mid-l+1; 30 for (RE int i=l;i<=r;i++) if (f[i][d]<sorted[mid]) lsame--; 31 int lpos=l,rpos=mid+1,resame=0; 32 for (RE int i=l;i<=r;i++) 33 { 34 if (i==l) num_left[i][d]=0; 35 else num_left[i][d]=num_left[i-1][d]; 36 if (f[i][d]<sorted[mid]) f[lpos++][d+1]=f[i][d],num_left[i][d]++; 37 else if (f[i][d]>sorted[mid]) f[rpos++][d+1]=f[i][d]; 38 else 39 { 40 if (resame<lsame) resame++,f[lpos++][d+1]=f[i][d],num_left[i][d]++; 41 else f[rpos++][d+1]=f[i][d]; 42 } 43 } 44 Build(l,mid,d+1); 45 Build(mid+1,r,d+1); 46 } 47 int Query(int L,int R,int l,int r,int d,int k) 48 { 49 if (l==r) return f[l][d]; 50 int s,ss; 51 if (L==l) s=num_left[r][d],ss=0; 52 else s=num_left[r][d]-num_left[l-1][d],ss=num_left[l-1][d]; 53 int mid=(L+R)>>1; 54 if (s>=k) return Query(L,mid,L+ss,L+ss+s-1,d+1,k); 55 else 56 { 57 int bb=(l-1)-L+1-ss; 58 int b=r-l+1-s; 59 return Query(mid+1,R,mid+1+bb,mid+bb+b,d+1,k-s); 60 } 61 } 62 63 int main() 64 { 65 scanf("%d%d",&n,&m); 66 for (RE int i=1;i<=n;i++) scanf("%d",&f[i][0]),sorted[i]=f[i][0]; 67 sort(sorted+1,sorted+1+n); 68 Build(1,n,0); 69 int s,t,k; 70 while (m--) 71 { 72 scanf("%d%d%d",&s,&t,&k); 73 printf("%d\\n",Query(1,n,s,t,0,k)); 74 } 75 return 0; 76 }
划分树的效率就很高了:

解法四 主席树(+离散化)
考虑一个问题:查询$[1,n]$中的第$K$小值
我们先对数据进行离散化,然后按值域建立线段树,线段树中维护某个值域中的元素个数。
在线段树的每个结点上用$cnt$记录这一个值域中的元素个数。
那么要寻找第$K$小值,从根结点开始处理,若左儿子中表示的元素个数大于等于$K$,那么我们递归的处理左儿子,寻找左儿子中第$K$小的数;
若左儿子中的元素个数小于$K$,那么第$K$小的数在右儿子中,我们寻找右儿子中第$K$-(左儿子中的元素数)小的数。
那么我们回到题目:查询区间$[L,R]$中的第$K$小值
我们按照从$1$到$n$的顺序依次将数据插入可持久化的线段树中,将会得到$n+1$个版本的线段树(包括初始化的版本),将其编号为$0~n$。
可以发现所有版本的线段树都拥有相同的结构,它们同一个位置上的结点的含义都相同。
考虑第$i$个版本的线段树的结点$P$,$P$中储存的值表示$[1,i]$这个区间中,$P$结点的值域中所含的元素个数;
假设我们知道了$[1,R]$区间中$P$结点的值域中所含的元素个数,也知道$[1,L-1]$区间中$P$结点的值域中所包含的元素个数,显然用第一个个数减去第二个个数,就可以得到$[L,R]$区间中的元素个数。
因此我们对于一个查询$[L,R]$,同步考虑两个根$root[L-1]$与$root[R]$,用它们同一个位置的结点的差值就表示了区间$[L,R]$中的元素个数,利用这个性质,从两个根节点,向左右儿子中递归的查找第$K$小数即可。

1 #include<map> 2 #include<set> 3 #include<ctime> 4 #include<cmath> 5 #include<queue> 6 #include<stack> 7 #include<cstdio> 8 #include<string> 9 #include<vector> 10 #include<cstdlib> 11 #include<cstring> 12 #include<iostream> 13 #include<algorithm> 14 #define LL long long 15 #define RE register 16 #define IL inline 17 using namespace std; 18 const int N=100000; 19 const int INF=2e9; 20 21 int n,m; 22 struct node 23 { 24 int key; 25 node *child[2]; 26 }smg[N*20],*pos=smg; 27 node *root[N+5]; 28 struct tt 29 { 30 int num,id,pos; 31 }a[N+5]; 32 int rem[N+5]; 33 34 IL bool comp(tt a,tt b) {return a.num<b.num;} 35 IL bool accomp(tt a,tt b) {return a.pos<b.pos;} 36 37 void Insert(node *&rt,int l,int r,int k) 38 { 39 node *x=rt; 40 rt=++pos; 41 rt->child[0]=x->child[0]; 42 rt->child[1]=x->child[1]; 43 rt->key=x->key+1; 44 if (l==r) return; 45 int mid=(l+r)>>1; 46 if (k<=mid) Insert(rt->child[0],l,mid,k); 47 else Insert(rt->child[1],mid+1,r,k); 48 } 49 int Query(node *lr,node *rr,int l,int r,int k) 50 { 51 if (l==r) return l; 52 int t=rr->child[0]->key-lr->child[0]->key; 53 int mid=(l+r)>>1; 54 if (k<=t) return Query(lr->child[0],rr->child[0],l,mid,k); 55 else return Query(lr->child[1],rr->child[1],mid+1,r,k-t); 56 } 57 58 int main() 59 { 60 scanf("%d%d",&n,&m); 61 for (RE int i=1;i<=n;i++) scanf("%d",&a[i].num),a[i].pos=i; 62 sort(a+1,a+n+1,comp); 63 a[0].num=-INF; 64 for (RE int i=1;i<=n;i++) a[i].id=a[i-1].id+(a[i].num!=a[i-1].num),rem[a[i].id]=a[i].num; 65 sort(a+1,a+n+1,accomp); 66 67 root[0]=pos; 68 root[0]->child[0]=root[0]->child[1]=pos; 69 root[0]->key=0; 70 71 for (RE int i=1;i<=n;i++) 72 { 73 root[i]=root[i-1]; 74 Insert(root[i],1,n,a[i].id); 75 } 76 77 int s,t,k; 78 while (m--) 79 { 80 scanf("%d%d%d",&s,&t,&k); 81 int tmp=Query(root[s-1],root[t],1,n,k); 82 printf("%d\\n",rem[tmp]); 83 } 84 return 0; 85 }
效率:

解法五 整体二分(+树状数组)
我们将询问离线,我们每次二分值域,然后用类似于“划分树”的思路,将询问分为两类:
区间内元素个数在$[L,mid]$的个数大于等于$k$和小于$k$。
如果大于等于$k$则应该取更小值(或有更小值可以去选(因为我们二分出来的并非准确值)),之后在$[L,mid]$中讨论;
如果小于$k$则应该取更大值,我们将$k-cnt$,之后在$[mid,R]$中讨论。
整体二分递归实现。
 POJ 2104 K-th Number (主席树)
POJ 2104 K-th Number (主席树)
