2017清北学堂集训笔记——动态规划Part2
Posted Memoryヾノ战心
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2017清北学堂集训笔记——动态规划Part2相关的知识,希望对你有一定的参考价值。
啊~到下午啦,我们进入Part2!——一个简洁的开头
我们来探讨第一类问题——路径行走问题
经典例题:方格取数(Luogu 1004)
设有 N*N 的方格图 (N<=9),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 0。
* 某人从图的左上角的 A 点出发,可以向下行走,也可以向右走,直到到达右下角的 B 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字 0)。
* 此人从 A 点到 B 点共走两次,试找出 2 条这样的路径,使得取得的数之和为最大。
- 与数字金字塔很类似?如果只走一次呢?
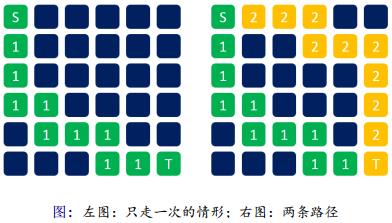
* 只走一次:(仿照数字金字塔)记录 F[i][j] 为走到第 i 行第 j 列的最大值。
- 思考:转移的顺序?转移的方程?
* 问题:在这道题目当中我们不能直接套用走一次的方法;一个方格只能被取走一次(也就是说每个权值只能被取用一次)。
- 考虑两条道路同时进行:状态 F[i][j][k][l] 来记录第一条路径走到(i,j),而第二条路径走到 (k,l) 的最大值。 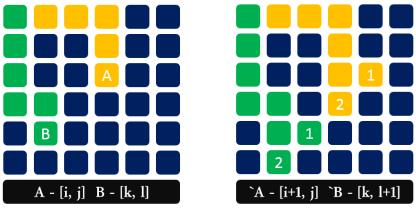
* 转移方程:考虑逆推(我可能是由哪些状态得到的)。
在这里,我们要保证这两个点所走的步数是相同的,那么这个状态才是有意义的,在这里没有这样算,不算也是对的,算了也不影响答案。。
- 每个点可以往下走或者往右走;一共走到有 2*2=4 种可能性(时刻注意边界情况)

1 //T11:方格取数(DP/逆推) 2 for(int i=1;i<=n;++i) 3 for(int j=1;j<=n;++j) 4 for(int k=1;k<=n;++k) 5 for(int l=1;l<=n;++l) 6 { 7 //注意,如果走到了一起,只加一次 8 int cost=a[i][j]+a[k][l]-a[i][j]*(i==k&&j==l);//如果两个位置是重叠的,就要减去重复的 9 //四种可能性;考虑:为什么不加边界情况的判断? 10 f[i][j][k][l]=max(max(f[i-1][j][k-1][l],f[i-1][j][k][l-1]),max(f[i][j-1][k-1][l],f[i][j-1][k][l-1]))+cost; 11 }
最长不下降子序列问题:
经典例题:导弹拦截(Luogu 1020)
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
* 输入导弹依次飞来的高度(雷达给出的高度数据是不大于 30000 的正整数),计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
-389 207 155 300 299 170 158 65
-最多能够拦截: 6;最少要配备: 2
* LIS:一个序列当中一段不下降的子序列。
* 这道题目中第一问要求我们找到一段最长的单调下降的子序列。 (无论是上升还是下降,可以使用类似的算法解决)
* 状态:我们用 F[i] 代表,以i 位置为结尾的一段, 最长的下降子序列的长度。
! 最优性:如果某段 [q1q2q3 ...qn] 是以qn结尾的最长下降子序列;那么去掉最后一个的序列 [q1q2q3...qn-1],依然是以qn-1结尾的最长下降子序列。(一个这是一个全局最优,每一步的最优解构成全局最优,所以拆成部分还是最优解,满足无后效性原则)
* 逆推:假设我们需要求以 X 结尾的最长下降子序列 F[X];
* 由最优性可得,我们除去最后一个位置(也就是 X),还是一段最长下降子序列。
* 那我们可以枚举这个子序列的结尾 Y,最优值就是 F[Y]。
! 但需要注意的是,必须保证A[X] < A[Y], X 比 Y 要低,才满足下降的要求。
* 我们从所有枚举的结果中找到一个最大的即可
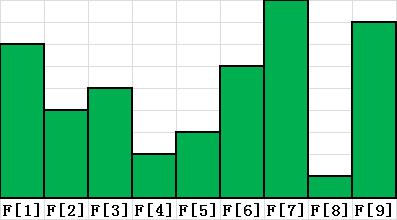
例如:我们看到这坨绿油油的图,我们讨论F[8]作为谁的结尾,由图中我们可以得到:
F[8]=F[4]+1(F[8]可以作为F[4]的结尾); F[8]=F[6]+1(F[8]同样可以作为F[6]的结尾); F[8]=F[7]+1(F[8]可以作为F[7]的结尾)
但是最长的还是F[8]作为F[4]结尾,这时候最长,取max
* 注意到题目还需要计算‘如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。’
* 可以直接观察得到,所求的答案至少为原题的最长不下降子序列。
- 因为它们当中,任意两个都不可能被同一个导弹打中。
- 事实可以证明,这就是答案。—— 啊喂?不给个证明嘛→_→?那肯定给啊!证明如下!
证明:因为假设一个导弹a被打中了,那么下次有比它高的导弹b,就没办法用打中a的导弹系统来打b,必须增加一个导弹系统,所以为最长不下降子序列长度。
同样地,我们还可以运用极限思维来考虑,有n颗导弹,它们的高度都是单调递增的,那么这时就必须要n个系统来拦截,所以为最长不下降子序列长度=n;
1 //T12:导弹拦截(DP/LIS/逆推) 2 int ansf=0,ansg=0;//记录所有的f(g)中的最优值 3 //f计算下降子序列,g计算不下降子序列 4 for(int i=1;i<=n;++i) 5 {////枚举倒数第二个,寻找最长下降放到f中,最长不下降放到g中 6 for(int j=1;j<i;++j) 7 if(a[j]>a[i]) f[i]=max(f[i],f[j]); 8 else g[i]=max(g[i],g[j]); 9 ++f[i],++g[i];//加上自己的一个 10 ansf=max(ansf,f[i]); 11 ansg=max(ansg,g[i]); 12 } 13 cout<<ansf<<endl<<ansg<<endl;//输出答案
问题变形:
经典例题:合唱队形(Luogu 1091)
*N位同学站成一排,音乐老师要请其中的(N-K)位同学出列,使得剩下的 K 位同学排成合唱队形。
*合唱队形是指这样的一种队形:设 K 位同学从左到右依次编号为1,2,…,K,他们的身高分别为T1,T2,...,TK,则他们的身高满足T1<...<Ti>Ti+1>...>TK(1≤i≤ K)。
* 你的任务是,已知所有 N 位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
- 186 186 150 200 160 130 197 220
- 最少需要 4 位同学出列
所谓合唱队形,就是要一个队列高度构成一个山峰的形状,有顶尖,两边单调递减。
我们可以采用枚举每个人为顶尖,从那个定点开始,向左、右寻找单调递减序列的最大和,这样。。。真的很麻烦。
* 问题转化:最少的同学出列 -> 尽量多的同学留在队列
* 与 LIS 的联系:如果确定了中间的“顶尖” ,两侧就是“单调上升” 和“单调下降” 的。 
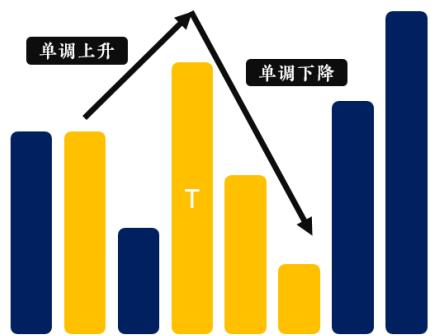
* 状态设计: F[i] 与 G[i](预先处理)
- F[i]:以 i 为端点,左侧的最长的上升子序列长度。
- G[i]:以 i 为端点,右侧的最长的下降子序列长度。
这个思路就是要我们找到每个以第i个点为末端的最长上升子序列和最长下降子序列,最终我们枚举每一个点i访问f[i]、g[i],找出两者相加最大值即可。
同样,我们还有另一种思路,找到了最长上升子序列和最长下降子序列,两个序列合并,去掉中间重复的元素(出现顶尖),即为答案。(这里我就不粘代码了,详见我之前写这个题的博客吧→_→)
1 //T13:合唱队形(DP/LIS/逆推) 2 for(int i=1;i<=n;++i) cin>>a[i],f[i]=g[i]=1; 3 for(int i=1;i<=n;++i) 4 for(int j=1;j<i;++j) 5 if(a[i]>a[j]) f[i]=max(f[i],f[j]+1); 6 for(int i=n;i;--i)//g的计算从反方向进行枚举 7 for(int j=n;j>i;--j) 8 if(a[i]>a[j]) g[i]=max(g[i],g[j]+1); 9 int ans=0; 10 /*把最长上升和最长下降的一部分部分拼在一起求总长度最大*/ 11 for(int i=1;i<=n;++i)//枚举每一个顶点为顶尖 12 { 13 ans=max(ans,f[i]+g[i]-1);//"-1"表示减掉顶尖这个重复计算的点 14 }
最长公共子序列:
经典例题:排列LCS问题(Luogu 1439)
* 给出 1-n 的两个排列 P1 和 P2,求它们的最长公共子序列。
* 公共子序列:既是 P1 的子序列,也是 P2 的子序列。
- 3 2 1 4 5
- 1 2 3 4 5
- 最长公共子序列 (LCS): 3([1 4 5])
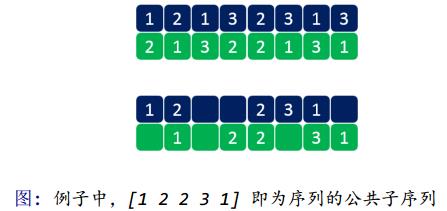
* LCS:两个序列的最长公共子序列。
* 状态:我们用 F[i][j] 代表,前一个序列以 i 位置为结尾,后一个序列以 j 位置为结尾,它们的最长公共子序列。
! 最优性:如果某段 [q1q2q3...qn] 是分别以i,j结尾的最长公共子序列;那么去掉最后一个的序列 [q1q2q3...qn-1],依然是以 i - 1; j - 1结尾的最长公共子序列。
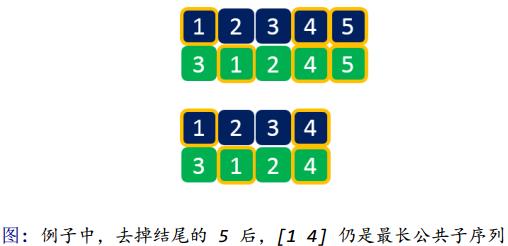
* 逆推:假设我们需要求两个序列分别以 i,j 结尾的最长公共子序列F[i][j],接下来我们可以分几种情况讨论:
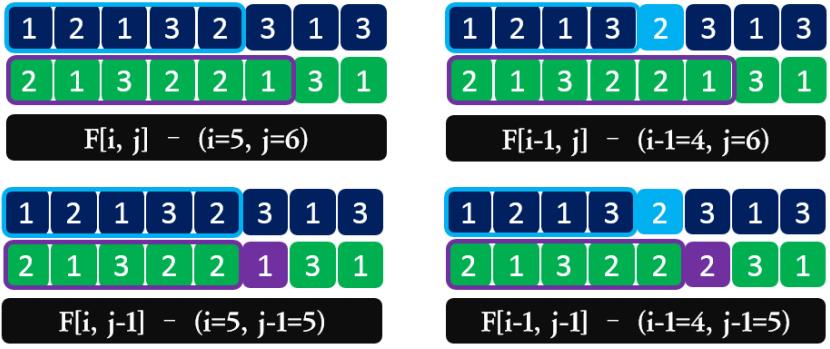
- A[i] 不在公共子序列中,那么长度则等于 F[i-1][j];
- B[j] 不在公共子序列中,那么长度则等于 F[i][j-1];
- A[i] 与 B[j] 都在子序列中,并且两者匹配,那么长度等于F[i-1][j-1]+1;
* 我们从所有枚举的结果中找到一个最大的即可。
* 逆推:假设我们需要求两个序列分别以 i,j 结尾的最长公共子序列F[i][j],可能的三种情况:
1 //T16:排列LCS问题(DP/LCS/50分数据规模限制) 2 for(int i=1;i<=n;++i) 3 for(int j=1;j<=n;++j) 4 { 5 //分三种情况进行讨论 6 f[i][j]=max(f[i-1][j],f[i][j-1]);//如果两个相同,娶一个最大值 7 if(p[i]==q[j]) f[i][j]=max(f[i][j],f[i-1][j-1]+1); 8 } 9 int ans=f[n][n];
仅仅在这个问题中,LCS是可以转化为LIS的:
* 假定某一个序列为 [1 2 3 ... N],那么答案则是另一个序列的 LIS;(因为满足严格的单调性质)
- 3 2 1 4 5
- 1 2 3 4 5
* 但如果两个序列都不是 [1 2 3 ... N] 呢?通过转化使一个序列变成它(过程为:我们把第一个序列的第一个数5变成1,第二个序列的1变成5;把第一个序列的第二个数3变为2,第二个序列的2变为3,以此类推...),而答案不变。
- 5 3 4 1 2 -> 1 2 3 4 5
- 3 5 1 2 4 -> 2 1 4 5 3
这种转换只能用在所给序列有不重复元素,长度相同,如果不满足,就会出现重复,会出错。
问题变形:
经典例题:字串距离(Luogu 1279)
暑假清北学堂集训笔记