清北学堂Day5

Posted 2020-10-09 小蒟蒻

Part1--模拟题

今天上午的题……怎么说呢，因为昨天晚上没睡好，所以随便搞了搞就睡觉了……emmm……而且今天的题有点偏数学，有找规律的，有概率的等等，感觉如果在noip中考的话，也应该是比较难我不会做的哪一类……所以……还是补觉比较实在。

---

Part2--今日专题：数论

今天应该是5天来听得最痛苦的一天了。一方面是状态也不好，另一方面，数论这个东西，本来就跟天书一样。所以我挑了一些比较实（jian）用（dan）的部分记了下来。

1.模运算

快速幂：a^b%c

 1 //快速幂(用乘法算幂)
 2 int pow(int a,int b,int p)
 3 {
 4     if(b==0) return 1%p;
 5     int c=pow(a,b/2,p);
 6     c=c*1LL*c%p; //转long long 
 7     if(b&1) c=c*a%p;
 8     return c;
 9 }
10 int pow(int a,int b,int p) //另一种写法 
11 {
12     int ret=1%p;
13     while(b)
14     {
15         if(b&1) ret=ret*a%p;
16         b>>=1;
17         a=a*a%p;
18     }
19     return ret;
20 }

慢速乘

 1 //慢速乘（用加法算乘）
 2 int mul(int a,int b,int p)
 3 {
 4     int ret=0;
 5     while(b)
 6     {
 7         if(b&1) ret=(ret+a)%p;
 8         b>>=1;
 9         a=(a+a)%p;
10     }
11     return ret;
12 }

2.素数 O(sqrt(n))来判断素数  for i=2~sqrt(n)

算数基本定理，唯一分解定理：任何一个大于1的自然数N，如果N不为素数，那么N可以唯一分解成有限个素数的乘积。

筛素数：（1）O(nlogn):埃式筛法

1 //筛素数O(nlogn):n/1+n/2+...+n/n=nlogn
2 bool vis[100000];
3 for(int i=2;i<=n;i++)
4 {
5     if(!vis[i])
6     {
7         for(int j=2;j*i<=n;j++) vis[j*i]=1;
8     }
9 }

（2）O(n)线性筛：

 1 //线性筛素数O(n)*****
 2 int mindiv[],prime[],tot;  //mindiv最小素因子，prime记录素数，tot记录素数数量 
 3 for(int i=2;i<=n;i++)
 4 {
 5     if(!mindiv[i]) mindiv[i]=i,prime[tot++]=i;  //得到素数 
 6     for(int j=0;prime[j]*i<=n;j++)
 7     {
 8         mindiv[prime[j]*i]=prime[j];
 9         if(prime[j]!=mindiv[i]) break;  //a1>1
10     }
11     //a1==1
12 }

3.最大公约数

如果两个数的最大公约数是1，则称为‘互素’

辗转相除法：

1 //辗转相除 O(logn)
2 int gcd(int a,int b)  //a,b的大小关系无所谓 
3 {
4     return b==0?a:gcd(b,a%b);
5 } 

4.费马小定理：对于一个素数，他的额p-1次方是1

即，若p为素数，a^p-1%p=1

证明：

%p能得到的所有结果：(0),1,2,3,…,p-1

每个数都*a à a,2a,3a,…,(p-1)a  mod p

假设xa=ya(即有重复) mod p

xa-ya=0 mod p

a(x-y)=0 mod p X

因此证明没有重复。      （然而证明并没有什么琴梨用）

5.Pick定理：一个计算顶点在格点上的多边形面积公式

S=a+b/2-1

6.矩阵乘法

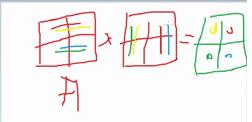
代码实现：

 1 Int a[][];
 2 
 3 Int b[][];
 4 
 5 Int c[][];
 6 
 7 For(int i=1;i<=n;i++)
 8 
 9 For(int j=1;j<=n;j++)
10 
11     For(int k=1;k<=n;k++)
12 
13         C[i][j]+=a[i][k]*b[k][j];

用处：有些转移方程或递推式可以写成矩阵模式（利用转移矩阵）

 

嗯今天就这样吧，实在是太难了/手动再见