极限运动

Posted 2023-05-17

大家都看过特种兵挂着一条绳子从楼顶滑下来吧、
1.我想知道那种绳子是哪种的什么地方能买到、
2.那些技能在攀岩俱乐部有教吗？
3.没有的话告诉下哪样的俱乐部有教。收费的没事

　　1.一般用户外或者攀岩的绳子，在户外用品店和户外俱乐部都有卖，价钱一般为20—30元/米（牌子是BEAL），不建议为了省钱买国产的，更不建议去淘宝上买，毕竟是生命问题

　　2.攀岩俱乐部一定会教，那是基础动作，与保护员动作相仿；户外俱乐部会选择性的教

　　3.同上攀岩俱乐部、户外俱乐部~

　　以下为一些资料：

　　你说的特种兵挂着一条绳子从楼顶滑下来的动作在户外运动及攀岩界一般称为【绳降】。

　　绳降Abseil.是快速下降的方式，但有内在的危险性。
　　绳降可以使用专门的下降器或绕身下降，前者易于掌握，后者因只需要最少的器材，更为灵活。

　　绳降对绳子没有很特殊的要求，依需要可选择单绳、双绳或组合绳组，一般攀岩和户外用的绳子都可以在一定的限度上进行绳降。
　　至于绳结，会以绳降的距离，速度要求，障碍物危险度，实时天气等多方面因素进行选择，总之一切以安全为原则。其中布林、双渔夫、八字结是较常用的绳结。

　　绳降的整个过程一般由有经验的户外运动人员进行操作，严谨地遵循绳降的基本操作即可完成一般岩壁的绳降，较为安全及专业的绳降应但按照如下操作：
　　1.绳降基本装备：
　　最小配置：登山绳，小绳套或扁带，设置下降锚点的装备；
　　建议配置：安全带，带锁定装置的主锁，下降器，抓绳结(作好的小绳套)，小锁。

　　2.绳降基本步骤：
　　(1).观察和规划下降路线和操作
　　观察岩壁或山坡的角度、高度、形态、植被等。
　　估测高度、角度的方法。可利用简单的3角知识。
　　角度小(30-60度)、距离短(一个绳距Pitch之内)的情况可以直接采用绕身下降的方式。但由于绕身下降不使用安全带，必须双手控制绳索，一旦发生意外，双手是很难腾出来的(有办法，但比较困难不易掌握)。所以这种方式必须严格训练、熟练掌握，而且对路线非常有把握的情况下才能使用。
　　角度大、路线长的情况，就要仔细规划。
　　首先，确定路线能够顺利的分段，每段之间的距离必须小于下降的可用绳长。确定你携带的锚点设备(以扁带、绳套为主)数目足够。
　　第二，确定每段都有稳妥可靠的下降锚点，比如粗壮的树(活的)，大丛灌木，形状合适的岩石(岩片、岩角、穿通的岩洞等等)，或者可靠的人工锚点，比如攀岩路线上的膨胀栓，或者可以自己设置坚固的锚点(利用裂缝放置岩锥、岩塞、机械塞等)。
　　第三，确定路线的安全性。路线上是否有不稳定的石头？是否茂密的灌木会影响下降和抽绳？路线是否不能够连成一个基本垂直的线路，而要求必须横移？是否会造成危险的摆荡，摆荡的情况下是否会切割绳子？路线上是否有明显的仰角或屋檐，使下降者脱离岩壁？上述这些问题都必须充分考虑。

　　(2).实施
　　(A)穿安全带，队友之间互相检查。即使你是菜鸟而对方是Lyn Hill(她曾经因为安全带脱开坠落20多米幸而被岩壁的一棵树挂住才得以幸存)。
　　(B)设置锚点。将绳套套在树上或大块的岩石上。如果岩石上的绳套看起来有向某侧滑动的趋势，就考虑用双套结系紧并加上抑制滑动的反向拉力。在岩角和岩片上的绳套都使用双套结。绕在大丛灌木的绳套，可使用单套结，或者绕2圈拉其中的一圈，这样都是绳圈越受力，树丛捆的越紧，避免只有树丛一侧受力的情况。
　　(C)设置备份锚点。原则上下降应使用至少2个均衡受力的锚点，但由于某些原因，比如器材不够了，被迫使用单锚点下降。这种情况下，备份锚点是不受力的。后下降的人应密切注意主锚点的情况，确认安全后，最后下降的人才拆掉备份锚点。
　　(D)将自己固定在锚点上。注意你的下降站可能只有很小一块地方，考虑到你同伴的数量，合理的分配空间。你可以用扁带或小绳套或菊绳将自己固定在锚点上。你的同伴也这样做。确定你们互相之间不会妨碍。特别注意：1、不要把自己的锁具直接扣入别人的锁中，否则对方如果想移动就比较困难；2、希望先移动的人的锁在上面(后扣入)，避免被同伴的锁“压死”。
　　(E)装下降器。注意不要脱手。或者使用单环结。
　　(F)设置后备措施。用一个短的(15-30cm)的绳套在下降器下方绕在绳子上做一个“法式抓结”并用小锁扣入腿带中。下降时制动手(下方手)轻捋抓结即可下降，而一但手送开就可以锁住身体。法式抓结不要做的太紧，好处是锁住之后不需很大的劲就可以打开。如果是用8字或单环结的双绳下降，因为扭绳子比较严重，法式抓结可能不太好用。单根绳一般没问题。
　　(G)下降。
　　(H)到达下一个下降站。重复(B)(C)(D)。确认已将自己稳妥的固定好，解开下降器和法式抓结。
　　(I)所有队员依次下降。(D)。
　　(J)确认路线上没有卡绳子的地方，也没有会带下来的石头之类。如果路线穿过灌木丛，建议使用一根绳对折下降，因为两根绳结起的绳结可能会卡在灌木丛中。抽绳子。
　　(K)开始下一段下降。

　　3.杂项：安全和效率
　　(1)绳尾打结。为了防止制动手失控的情况下一坠到底，绳尾打结是有效的办法。但在抽绳的时候一定要注意解开。
　　(2)长头发的人应盘起来，避免绞入下降器中。
　　(3)减小抽绳的拉力。如果绳子搭在岩台上，抽绳会比较费劲，可以通过延长扁带的方式，使绳子延伸到岩台下面。
　　(4)背大包的队员先下，空身和体重最轻的队员最后下。
　　(5)如果背包很重，会坠的上身后仰，容易出危险。可交叉背一条胸带，在胸前扣一把锁，绳子扣入锁中就可以有效的控制身体姿态。

参考资料：http://zhidao.baidu.com/question/134498548.html

参考技术A 1:淘宝
2：有的，要花大概100~200 看时间 一般1小时100
3：- -同上

目标运动模型——匀速运动CV

目标运动模型-——匀速运动CV

原创不易，路过的各位大佬请点个赞

WX: ZB823618313

目标运动模型-——匀速运动CV

• 目标运动模型-——匀速运动CV
• • 1. 目标模型概述
  • 2. 目标运动模型
  • • 2.1 匀速运动CV模型
    • • 2.1.1 一维匀速运动CV 模型
      • 2.1.2 二维匀速运动CV 模型
      • 3.1.1 三维匀速运动CV 模型
    • 3.2 匀加速运动CA模型
    • 3.3 匀速转弯CT模型
    • 3.4 Singer模型
    • 3.5 “当前”统计模型
    • 3.6 Jerk统计模型

1. 目标模型概述

  机动目标模型描述了目标状态随着时间变化的过程。一个好的模型抵得上大量的数据。当前几乎所有的目标跟踪算法都是基于模型进行状态估计的。在卡尔曼滤波器被引入目标跟踪领域后，基于状态空间的机动目标建模成为主要研究对象之一。

1. 目标的空间运动基于不同的运动轨迹和坐标系
   一维运动
   二维运动
   三维运动

2. 根据不同方向的运动是否相关
   坐标间不耦合模型
   坐标间耦合模型

坐标间不耦合模型： 这类模型假设三维空间三个正交方向上的目标机动过程不耦合。目标机动是飞行器受到外力作用而使得加速度变化所致，所以对机动建模的难点在于对目标加速度的描述。对于无机动目标，常速(Constant Velocity，CV〉模型常用于描述这类目标的运动，而常加速度(Constant Acceleration，CA）模型则常用于描述加速度趋近常数的机动目标的运动。

坐标间耦合模型： 坐标间耦合模型绝大多数情况下指的是转弯运动模型。由于此类模型与坐标密切相关，所以可以分为两类:二维转弯模型和三维转弯模型。二维转弯模型又称为平面转弯模型，即CT模型。

下面讲机动目标不同的模型：

2. 目标运动模型

2.1 匀速运动CV模型

匀速运动模型用来匹配目标做匀速直线运动的情况，这也是目标运动最简单的情况.
其中匀速运动模型包括：

一维匀速运动CV 模型

二维匀速运动CV 模型
三维匀速运动CV 模型

2.1.1 一维匀速运动CV 模型

由于目标做匀速直线运动，则目标加速度为0。实际情况中，速度至少要轻微的变化，则加速度常常看做是具有随机特性的扰动输入，可用连续时间的白噪声来建模，并假设其服从均值为零，方差为的高斯分布，即
$$\ddot{X}(t)=W(t)$$
其中$W(t)$零均值白高斯噪声最为普遍。

一维匀速运动模型(连续)：
目标状态为：位置和速度、即$$X=[x,\dot{x}{]}^T$$

CV模型为：
$$\dot{X}(t)=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]X(t)+\left[\begin{array}{c}0\\ 1\end{array}\right]W(t)$$

离散化上述模型：

一维匀速运动模型(离散)：
$$X_{k+1}=\left[\begin{array}{cc}1& T\\ 0& 1\end{array}\right]X_k+\left[\begin{array}{c}{T}^2/2\\ T\end{array}\right]W_k$$
$T$为采样时间。

一维匀速运动CV目标航迹如下：

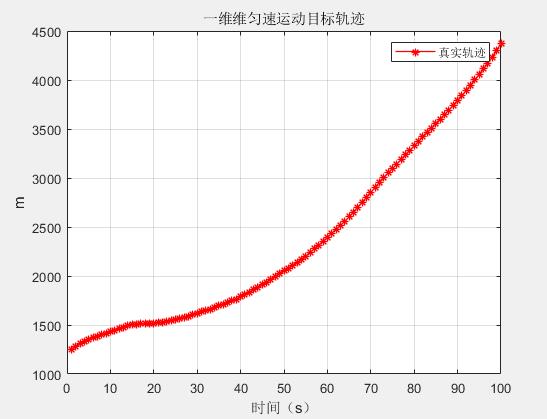
代码

%% 一维匀速CV运动目标轨迹       
clc;
clear all;
close all;
n=2; % state dimension : 6
T=1; % sample time.
N=100; %the runs atime，跟踪总时长
w_mu=[0]';
%% target model
q=3; % 目标运动学标准差，过程噪声
Qk=q^2*eye(1);% cov. of process noise
% state matrix
Fk= [1 T
     0 T ]; %
 Gk= [ T^2/2  
       T      
       ]; %
   
   
% 
%% define parameter
sV=zeros(n,N,1,1); % state
x=[1000,20]';
P_0=diag([1e5,10^2]); 

x0=mvnrnd(x,P_0); % 初始状态
%x0=(x+normrnd(0,0.001)')';
x=x0';
for k=1:N
   %% %%%%%%% target model %%%%%%%%%%%%%%%%%%%%
   %% 目标运动学模型(被跟踪目标建模)，匀速运动CV模型
    w=mvnrnd(w_mu',Qk)';%过程噪声方差
    x=Fk*x+Gk*w;
    sV(:,k,1,1)=x;

end
% 一维匀速CV运动目标轨迹 
ii=1:N;
figure
plot(ii,sV(1,:,1,1),'-*r','LineWidth',1)
grid on
xlabel('时间（s）');ylabel('m');
legend('真实轨迹')
title('一维维匀速运动目标轨迹')

利用扩展卡尔曼滤波EKF跟踪上面的一维匀速运动目标，跟踪轨迹如下

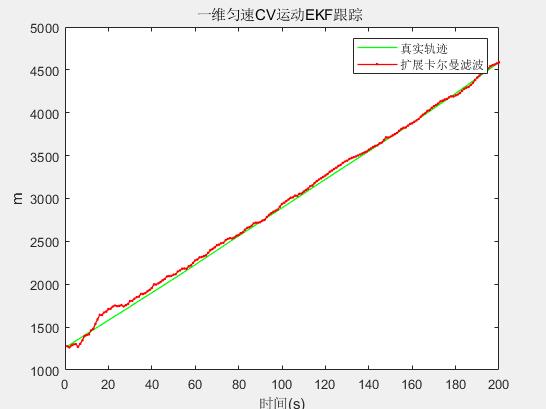
2.1.2 二维匀速运动CV 模型

二维匀速运动模型(连续)：
目标状态为：x维位置和速度、y维位置速度、即$$X=[x,\dot{x}，y,\dot{y}{]}^T$$

CV模型为：
$$\dot{X}(t)=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 0& 0\end{array}\right]X(t)+\left[\begin{array}{cc}0& 0\\ 1& 0\\ 0& 0\\ 0& 1\end{array}\right]W(t)$$

离散化上述模型：

二维匀速运动模型(离散)：
$$X_{k+1}=\left[\begin{array}{cccc}1& T& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& T\\ 0& 0& 0& 1\end{array}\right]X_k+[\begin{array}{cc}{T}^2/2& 0\\ T& 0\\ 0& T极限符号\; Markdown\; LaTex\\ 0& \end{array}$$

极限定义理解

数学一：一函数，极限，连续

第1章：函数与极限

中心极限定理，大数极限定理

极限编程核心价值：尊重（Respect）